SOLIDE
EN MOUVEMENT DE ROTATION AUTOUR D’UN AXE
CALCUL DES MOMENTS D’INERTIE
Définition
Le moment d’inertie d’un solide
(noté ![]() ) est une grandeur physique qui caractérise
la répartition de la masse d’un solide autour d’un axe de rotation.
) est une grandeur physique qui caractérise
la répartition de la masse d’un solide autour d’un axe de rotation.
Il joue le même rôle que la masse en translation, mais
pour les mouvements de rotation.
Calcul des moments d’inertie :
-Circonférence pesante de masse m et rayon R :
![]()
-Disque et
cylindre homogène de masse m et de rayon R :
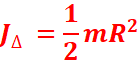
-Tige mince de
longueur l :
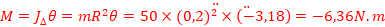
-Plaque rectangulaire de longueur a et de largeur
b :
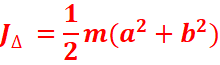
-sphère pleine et sphère creuse à parois minces de
rayon R:
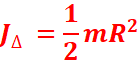
Théorème de Huygens :
Le moment d’inertie d’un
solide, par rapport à un axe quelconque Δ est la somme du moment d’inertie
: ![]() de ce solide par rapport à un axe ΔG parallèle à l’axe
Δ et qui passe par le centre d’inertie G du solide et du produit de la
masse m du solide par le carré de la distance d entre les axes Δ et ΔG.
de ce solide par rapport à un axe ΔG parallèle à l’axe
Δ et qui passe par le centre d’inertie G du solide et du produit de la
masse m du solide par le carré de la distance d entre les axes Δ et ΔG.
![]()
RELATION FONDAMENTALE DE
LA DYNAMIQUE DU SOLIDE EN ROTATION :
La somme des moments, par rapport à l’axe de rotation, des forces extérieures
appliquées à un solide en rotation est égale au produit du moment d’inertie du
solide par rapport à cet axe par l’accélération angulaire du solide.
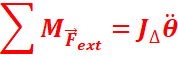
![]() Moment d’inertie en kg.m2.
Moment d’inertie en kg.m2.
![]() : accélération angulaire en rad.s-2
: accélération angulaire en rad.s-2
Exemple : soit une poulie de rayon r et de masse m=2 kg en
rotation autour d’un axe (Δ) passant par son centre O. On l’utilise pour soulever
une charge de masse M à l’aide d’un moteur non représenté. Calculer
l’accélération angulaire![]() .
.
On donne :
T=6 N, r =10 cm,
Système : poulie
Bilan des forces
Tension du fil :![]()
Poids de la poulie :![]()
Réaction de l’axe : ![]()
![]()
![]()
EXERCICES
EXERCICE
I :
Le tambour d’une machine à
laver le linge est un cylindre de 46 𝑐𝑚 de diamètre. Au
moment de
l’essorage, il tourne autour de son axe à 800 𝑡𝑟⁄𝑚𝑖𝑛.
1- Calculer sa vitesse angulaire 𝜔 de rotation
en 𝑟𝑎𝑑⁄𝑠 .
2- Calculer la vitesse v du point H de la périphérie du tambour.
EXERCICE
II:
1- Déterminer la vitesse angulaire de la grande aiguille d’une montre.
2- Déterminer la vitesse angulaire de la petite aiguille d’une montre.
3- On choisit l’origine des dates à midi. A quel instant les deux aiguilles se
superposent-elles à nouveau.
EXERCICE
III :
Deux solides S1 et
S2 de masses respectives m1 et m2 sont
reliés par un fil inextensible et de masse négligeable passant sur la gorge
d’une poulie de rayon r et de masse M, tournant sans frottement autour d’un axe
horizontal ∆ passant par son milieu. Le moment d’inertie de la poulie par
rapport à l’axe est J∆.
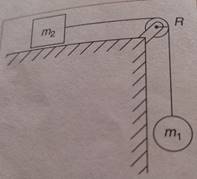
On
abandonne le système sans vitesse initiale.
1.
Déterminer l’accélération prise par le système.
2
Calculer les tensions T1 et T2 des cordes.
On donne
: J∆ = 0,5 Kg.m2 ; R = 0,3
m ; m1=4Kg ; m2=3
Kg
3
Quels résultats obtiendrait-on en négligeant l’inertie de la poulie ?
4.
Ecrire les équations horaires des mouvements de S1 et de S2.
EXERCICE
IV :
Une
platine de tourne-disque de moment d’inertie JΔ=22x10-3 kg.m2 est
lancée a la vitesse de
rotation de 33 tr/mn.
1.Calculer
sa vitesse angulaire.
2.On
coupe l’alimentation du moteur, La platine effectue 10 tours avant de
s’arrêter.
Calculer
la force de frottement supposée constante qui s’exerce au niveau de l’axe de
rotation.
EXERCICE
V :
Un
appareil de levage utilisé sur un chantier se présente de la façon
suivante :
-Un
cylindre creux B (toute sa masse est repartie à sa périphérie) homogène de
rayon R = 0,20 m et de masse m=50 kg peut tourner sans frottements autour de
son axe de révolution disposé horizontalement. Il est mû par un moteur
électrique qui exerce sur le cylindre un couple de moment constant M.
-
Un câble inextensible de masse négligeable est enroulé sur le cylindre, une
extrémité étant fixé au cylindre. A l’autre extrémité on suspend un corps A de
masse m’=1000kg. On prendra g=10m.s-2
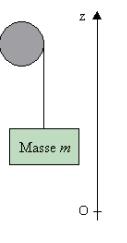
1-
Le corps s’élève en partant du repos ; le câble ne glisse pas sur le
cylindre.
1.1-Montrer
par deux manières différentes (en utilisant le théorème de l’énergie cinétique
à l’appareil de levage complet, puis sans utiliser ce théorème, mais en
considérant la tension T du câble) que le mouvement de A est uniformément
varié.
1.2-
A s’élève d’une hauteur h= 50m en un temps t=25 s ; calculer son
accélération.
1.3-
Calculer la tension du câble ; quel serait l’allongement d’un dynamomètre
de raideur k=105 N.m-1 intercalé entre A et le
câble ?
1.4-
Calculer le moment M du couple
moteur.
1.5-Calculer
le travail fourni par le moteur électrique lorsque A s’est élevé d’une hauteur
de 50 m.
2
– Au bout de 50m de montée la charge est délestée automatiquement sans à coup
et le moteur électrique débrayé. Le cylindre est alors arrêté en 10 tours sous
l’effet d’un couple de freinage de moment constant. Quelle est la valeur de ce
couple ?
CORRIGES :
EXERCICE I :
1- Vitesse angulaire 𝜔 de rotation du tambour :
𝜔 =2πN
𝜔 =800 ×
2𝜋 :60 ≈
84 𝑟𝑎𝑑⁄𝑠
2- Vitesse v d’un point de la périphérie du tambour :
𝑣 = 𝑅. 𝜔=
𝑣 =46.10-2/2
× 84
𝑣 ≈
19 𝑚⁄𝑠
EXERCICE II :
1- Vitesse angulaire de la grande aiguille d’une montre :
La période de rotation de la grande aiguille est : ∆𝑡 = 𝑇 = 60 𝑚𝑖𝑛 ⟹ 𝑇 = 3600𝑠
𝜔𝐺 =2𝜋 :𝑇
𝜔𝐺 =2𝜋 :3600 // un tour complet (2π) se
fait en 1h(3600s)
𝜔𝐺 ≈
1,75.10-3 𝑟𝑎𝑑⁄𝑠
2- Vitesse angulaire de la petite aiguille d’une montre :
La période de rotation de la petite aiguille est : ∆𝑡′ = 𝑇′ = 12 ℎ ⟹
𝑇′ = 12
× 3600𝑠 =
43200 𝑠
𝜔𝑃 =2𝜋𝑇
𝜔𝑃 =2𝜋 :43200
𝜔𝑃 ≈
1,45.10-4 𝑟𝑎𝑑⁄𝑠
3- A l’instant t, l’angle balayé par la grande aiguille est : 𝜃𝐺 = 𝜔𝐺. 𝑡
De même, à l’instant t, l’angle balayé par la petite aiguille est : 𝜃𝑃 = 𝜔𝑃. 𝑡
Les aiguilles sont superposées si :
𝜃𝐺 = 𝜃𝑃 + 2𝑘𝜋
𝜔𝐺. 𝑡 = 𝜔𝑃. 𝑡 + 2𝑘𝜋
𝑡 =2𝑘𝜋(𝜔𝐺 – 𝜔𝑃)
Les aiguilles se superposent un première fois pour 𝑘 = 1
𝑡 =2𝜋=1,75.10-3 - 1,45.10-4
𝑡 = 3927𝑠
𝑡 = 1ℎ𝑒𝑢𝑟𝑒 5 𝑚𝑖𝑛𝑢𝑡𝑒𝑠 𝑒𝑡 27 𝑠𝑒𝑐𝑜𝑛𝑑𝑒𝑠
EXERCICE III :
Système S2
T2=m2a
Système S1
T1=P-m1a=m1g-m1a
Poulie
T1r- T2r- = J∆![]() <=> T1- T2= J∆
<=> T1- T2= J∆![]()
<=> m2g=m2a+
m1a +J∆![]() = am2(1+
= am2(1+![]() + J∆
+ J∆ ![]() )
)
=> 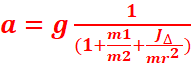
2 Tensions T1 et T2 des
cordes.
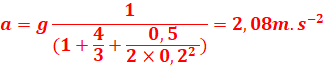
T1=m1a=4x2,08=8,33N
T2=P-m2a=3x10-3x2,08=23,82N
3 En négligeant l’inertie de la poulie :
J∆.=0 =>
![]() .
.
4. Equations horaires des mouvements de S1 et
de S2.
x1=1/2at2=2,04t2 (m) et v1=at=4,28t
x2=1/2at2=2,04t2 (m) et
v2=at=4,28t
Equations horaires du
mouvement de la poulie :
![]()
![]()
![]()
EXERCICE IV :
1.Vitesse angulaire.
![]()
2. La platine effectue 10 tours avant de s’arrêter, donc elle balaie
un angle
![]()
D’après le théorème de l’Energie cinétique
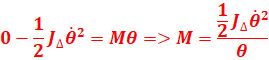
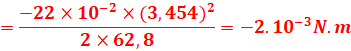
EXERCICE V :
1.1-
1ere méthode :
Système 1 : Masse M
T-P=Ma => T=m’g + m’a
Système 2 : Poulie
M – T’R= J∆![]() T’R=M
- J∆
T’R=M
- J∆![]()
T=T’ => m’g + m’a=![]() <=> a(m’+m)=
<=> a(m’+m)= ![]()
2eme méthode : Théorème de l’énergie cinétique.
Système 1 : Masse M
![]()
![]()
=> Th=![]()
![]()
Système 2 : Poulie
![]()
![]()
![]()
![]()
![]()
![]()
![]()
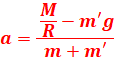
a est une constante donc le
mouvement de la masse m’ est rectiligne et
uniformément varie.
1.2- calcul de son accélération.
![]()
1.3- Calcul de la tension du câble.
T=m’g + m’a=1000x10
+1000x0,16=10000+16=10016N.
Allongement du dynamomètre.
![]()
1.4- Calculer le moment M du couple
moteur.
m’a +m’g
=M/R -ma
![]()
1.5-Calcul du travail
![]()
2 –Au moment de la rupture
a=0,16m/s2 soit 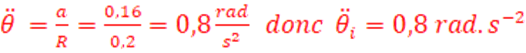
![]()
La relation indépendante du temps donne :
0 -![]() 3,18
3,18![]() .
.
C’est la décélération.
![]()
En utilisant le théorème de l’énergie cinétique.
- ![]() => M=
=> M=![]() =
=![]()
![]()
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire