NOMBRES COMPLEXES ET CONFIGURATIONS DU PLAN

Nombres complexes et configuration du plan

Vecteurs du plan

A et B sont deux points du plan.

· Les points A et B sont repérés :

-soit par leurs coordonnées (x_A ;y_A) ; (x_B ;y_B) 

-soit par leurs affixes : z_A ;z_B

De plus, on a :

· Le vecteur est repéré par :

-ses coordonnées : (x_B-x_A, y_B-y_A)

-son affixe :

Donc

Angles orientés

A, B, C, D sont 4 points du plan, la mesure de l’angle formé par les demi-droites (AB, CD) est donnée par :

(

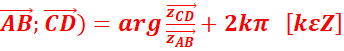
ou

(

Exemple :

A, B, C, D étant des points d’affixes respectives : Ѵ3 +2i ; Ѵ3+i ; -2i ;1-i ;

Calculons : (

On a:

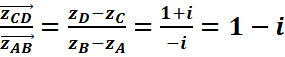
Donc :

=-

Quelques configurations base

Egalite de vecteurs

A, B, C, D sont 4 points du plan

Exemple : A, B, C, D étant des points d’affixes respectives : -Ѵ3+3i ; 2i ; -i ; Ѵ3-2i

Démontrons que ABCD est un parallélogramme.

On a:

Donc :

Egalite des distances

A, B, C, D sont 4 points du plan.

Exemple:

A,B,C étant des points d’affixes respectives :-i ;1+i ;1-3i

Démontrons que le triangle ABC est isocèle en A. 

On a:

d’où AB=CD

Alignement de trois points

A, B, C étant des points distincts du plan

Exemple :

A, B, C étant des points d’affixes respectives : -1-i ; 2+3i ; -10-13i

Démontrons que les points A, B, C sont alignes

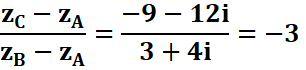
Orthogonalité de deux droites

A, B, C, D sont 4 points du plan

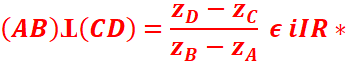
Droites parallèles

Propriété : A, B, C et D sont des points d’affixes respectives z_A , z_B , z_C et 𝑧_𝐷

tels que : A≠ B et C≠ D. Les droites (AB) et (CD) sont parallèles si et seulement si :

Triangles

A, B et C sont des points non alignés d'affixes respectives z_A , z_B et z_C .

- Le triangle ABC est rectangle en A si et seulement si :

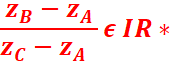
- Le triangle ABC est isocèle en A si et seulement si :

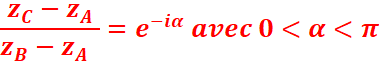
- Le triangle ABC est rectangle et isocèle en A si et seulement si :

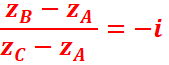
- Le triangle ABC est équilatéral si et seulement si :

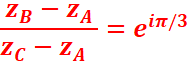
Ou

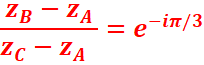
Transformations élémentaires du plan

Ecritures complexes de symétrie centrale de centre O et de symétries Orthogonales d’axes (OI) et (OJ)dans le repère(O,I,J).

Propriété

Le plan complexe est muni d’un repère orthonormé direct (O, I, J).

• La symétrie orthogonale d'axe (OI) a pour écriture complexe : 𝑧 ′ = 𝑧̅

• La symétrie centrale de centre O a pour écriture complexe : 𝑧 ′ = −𝑧

• La symétrie orthogonale d'axe (OJ) a pour écriture complexe : 𝑧 ′ = −𝑧̅

Ecriture complexe d’une translation, d’une homothétie et une rotation

• Translation de vecteur d'affixe b,

M et M' sont les points du plan d'affixes respectives z et z'. On a :

𝑀′ = t𝑢⃗ (𝑀) ⟺ 𝑀𝑀′ ⃗ = 𝑢⃗ . ⟺ 𝑧 ′ − 𝑧 = 𝑏 ⟺ 𝑧 ′ = 𝑧 + 𝑏

La translation de vecteur d’affixe b a pour écriture complexe :

𝑧 ′ = 𝑧 + 𝑏

• Homothétie de centre Ω et de rapport 𝑘, 𝑘 ∈ ℝ∗

h est l'homothétie de centre Ω d’affixe Z _Ω et de rapport 𝑘, 𝑘 ∈ ℝ∗ .

M et M' sont les points du plan d'affixes respectives z et z'.

On a :

𝑀′ = ℎ(𝑀) ⟺ Ω𝑀′ ⃗= 𝑘Ω⃗𝑀⃗

<= >Z’-Z_Ω = 𝑘(Z - Z_Ω)

<= >Z’=k(Z - Z_Ω) + Z_Ω

L'homothétie de centre Ω d’affixe Z _Ω et de rapport k a pour écriture complexe :

z’=k(z - z_Ω) + z_Ω

• Rotation de centre Ω et d’angle 𝜃,

𝜃 ∈ ]−𝜋, 𝜋]

r est la rotation de centre de centre Ω d’affixe Z_Ω et d'angle orienté de mesure principale 𝜃.

• M et M' sont les points du plan d'affixes respectives z et z' tels que M est distinct de Ω.

On a:

𝑀′ = 𝑟(𝑀) ⟺ Ω𝑀′ = Ω𝑀 et 𝑀𝑒𝑠(Ω𝑀; ⃗ Ω𝑀′ ̂) = 𝜃

• 𝑟(Ω) = Ω , le point Ω est invariant

On a :

z’−𝒛_Ω /𝒛−𝒛_Ω =𝒆 ^𝒊q => -z’=𝒆 ^𝒊q (z – z_Ω) + z_Ω

La rotation de centre Ω d’affixe z_Ω et d'angle orienté de mesure principale 𝜃 a pour écriture complexe :

z’= e^𝒊q (z – z_Ω) + z_Ω

EXERCICES

EXERCICE I:

On considère les points A(-2+3i), B(2+4i), C(5+3i), D(1+2i) et E (-7).

a. Démontrer que le quadrilatère ABCD est un parallélogramme.

Calculer l’affixe de son centre.

b. Les points D, C et E sont-ils alignés ?

EXERCICE II:

Le plan complexe est muni d’un repère orthonormé direct (O, u , v ).

On donne les points A, B, C, D, I, J et K d’affixes respectives 2 + 𝑖, 2 - 𝑖, 5 - 2𝑖, 5 + 2𝑖 ,1, i et 4. Justifie que :

1) Les droites (AB) et (CD) sont parallèles ;

2) Les points J, I et B sont alignés ;

3) Les droites (OK) et (DC) sont perpendiculaires ;

4) Le triangle JBD est rectangle en B ;

5) Les points A, B, C et D sont cocycliques.

EXERCICE III :

Le plan complexe est muni d’un repère orthonormé direct (O, I, J).

1) Détermine l’écriture complexe de l’homothétie h de centre Ω d’affixe − 1 − i et de rapport 3.

2) Détermine l’écriture complexe de la translation 𝑡 de vecteur u⃗ d’affixe 1 + 4𝑖.

3) Détermine l’écriture complexe de la rotation 𝑟 de centre A d’affixe 1 + 𝑖 et d’angle 2π/ 3.

EXERCICE IV :

Le plan complexe est muni d’un repère orthonormé direct (O ; I, J).

Détermine dans chaque cas, la nature et les éléments caractéristiques de la transformation 𝑓 du plan défini par son écriture complexe :

a) z’ = 5z + 2i

b) z’ = z + 1 + 3i

c) z’ = (1/ 2 + 𝑖 √3/2) z + 1 /2 − 𝑖 √3 /2

EXERCICE V :

1. Déterminer la transformation F du plan associée à la bijection complexe f définie par : f(z)=(1+iѴ3)z +3-i

2. Déterminer la transformation F du plan associée à la bijection complexe f définie par : f(z)=Ѵ2/2(1-i)z -i

3. Déterminer la transformation F du plan associée à la bijection complexe f définie par : f(z)=2z -3+i

4.Déterminer la transformation F du plan associée à l’homothétie h de rapport -3 et de centre le point Ω d’affixe 2+i.

5.Déterminer la bijection complexe f associée à la rotation r d’angle oriente de mesure π/6 et de centre le point Ω d’a affixe 1-i.

6. r est une rotation d’angle oriente de mesure π/4 et de centre le point A d’affixe 2i,

h une homothétie de rapport -2 et de centre le point B d’affixe -i

On désigne par F la transformation hor du plan.

Déterminer la bijection complexe f associée à F

CORRIGES

EXERCICE I :

a. -On va démontrer que les vecteurs sont égaux.

Affixe de

Affixe de

Donc et donc ABCD est un parallélogramme.

b.

- le centre du parallélogramme est le milieu I du segment [AC]. Son affixe est :

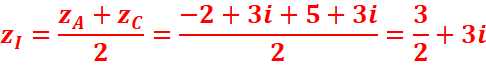
b.

On va démontrer que les vecteurs sont colinéaires.

Affixe de

Affixe de

Donc donc les vecteurs sont colinéaires et donc les points D, C et E sont alignes.

//

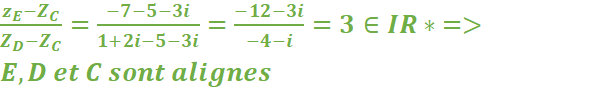
EXERCICE II :

On a : 𝑧_𝐷−𝑧_𝐶 /𝑧_𝐵−𝑧_𝐴 = 5+2𝑖−(5−2𝑖)/ 2−𝑖−(2+𝑖) = 4𝑖 −2𝑖 = −2 .

D’où : 𝑧_𝐷−𝑧_𝐶 /𝑧_𝐵−𝑧_𝐴 ∈ ℝ∗ ;

Par suite les droites (AB) et (CD) sont parallèles.

2) On a : 𝑧_𝐵−𝑧_𝐼/ 𝑧_𝐽−𝑧_𝐼 = 2−𝑖−1/ 𝑖−1 = - 1.

D’où : 𝑧_𝐵−𝑧_𝐼 /𝑧_𝐽−𝑧_𝐼 ∈ ℝ∗ .

Par suite les points J, I et B sont alignés.

3) On a : 𝑧_C−𝑧_D /𝑧_𝐾−𝑧_𝑂 = 5-2𝑖−(5+2𝑖) /4 = - 𝑖 .

D’où : 𝑧_C−𝑧_D /𝑧_𝐾−𝑧_𝑂 ∈ 𝑖 ℝ∗ .

Par conséquent les droites (OK) et (DC) sont perpendiculaires.

4) On a : 𝑧_𝐵−𝑧_𝐷/ 𝑧_𝐵−𝑧_𝐽 = 2−𝑖−(5+2𝑖)/ 2−𝑖−𝑖 = −3−3𝑖/2−2𝑖 = − 3/ 2 𝑖.

D’où : 𝑧_𝐵−𝑧_𝐷 /𝑧_𝐵−𝑧_𝐽 ∈ 𝑖 ℝ∗ .

Par suite le triangle JBD est rectangle en B.

5) On a : 𝑧_𝐷−𝑧_𝐶/ 𝑧_𝐷−𝑧_𝐴 : 𝑧_𝐵−𝑧_𝐶 /𝑧_𝐵−𝑧_𝐴 = 4𝑖 /3+𝑖 : −3+𝑖 /−2𝑖 = −4/ 5 .

D’où : 𝑧_𝐷−𝑧_𝐶 /𝑧_𝐷−𝑧_𝐴 : 𝑧_𝐵−𝑧_𝐶 /𝑧_𝐵−𝑧_𝐴 ∈ ℝ∗ .

Par suite les points A, B, C et D sont cocycliques.

EXERCICE III

h étant l’homothétie de centre Ω d’affixe −1 − i et de rapport 3, son écriture complexe est :

z ′ − (−1 − i) = 3(z − (−1 − i)).

Par suite, l’écriture complexe de l’homothétie h de centre Ω(−1 − i)

et de rapport 3 est : z ′ = 3z + 2 + 2i.

2) L’écriture complexe de la translation 𝑡 de vecteur u⃗ est :

z ′ = z + z_u⃗ . Or z_u⃗ = 1+4i

L’écriture complexe de la translation 𝑡 de vecteur u⃗ est : z ′ = z +1+4i.

3) L’écriture complexe de la rotation 𝑟 de centre A et d’angle 2π /3 est :

z ′ − (1 + i) = e i 2π/ 3 (z − (1 + i))

z ′ = ( −1 /2 + i √3 /2 )(z − (1 + i)) +1+i

z ′= ( −1/ 2 + i √3 /2 ) z + 3/2-√3/ 2 + i (3/2−√3/ 2)

L’écriture complexe de la rotation 𝑟 de centre A d’affixe 1 + i et d’angle 2π/ 3 est :

z ′ = ( −1 /2 + i √3 /2 ) z + 3/2-√3/ 2 + i (3/2−√3/ 2) .

EXERCICE IV :

Soit z’=az + b

a) a = 5, aÎ ℝ∗ \ {1}, 𝑓 est une homothétie de rapport 5.

Déterminons l’affixe z_Ω de son centre.

z’ = 5z + 2i;

z’=k(z - z_Ω) + z_Ω

z’=5 (z - z_Ω) + z_{Ω =} 5z + 2i

<=> 5z-5 z_{Ω +} z_Ω=5z+2i => zΩ =-2i/4 = -i/2

// z_Ω =𝑏 /1−𝑎 => z_Ω = 2𝑖 /1−5 = − 1/ 2 𝑖

Donc 𝑓 est l’homothétie de centre Ω d’affixe (− 1 /2 )𝑖 et de rapport 5.

b) a = 1 D'où, 𝑓 est la translation de vecteur d'affixe 1+3i.

c) a = 1 /2 + √3/ 2 𝑖, a Î ℂ ∖ ℝ et |1 /2 + √3/ 2 𝑖 | = 1.

Donc 𝑓 est une rotation.

- son angle : Arg(1 /2 + √3/ 2 𝑖) = 𝜋 /3

- son centre a pour affixe : 1 /2 −𝑖 √3 /2 /1−( 1 2 +𝑖 √3/ 2 ) = 1

z’= e^𝒊q (z – z_Ω) + z_Ω = e^𝒊q z – e^𝒊q z_Ω + z_Ω = e^𝒊q z -+ z_Ω(1- e^𝒊q) = ( −1/ 2 + i √3 /2 ) z + z_Ω(1- ( −1/ 2 + i √3 /2 ))

or z ′ − (1/ 2 + 𝑖 √3/2) z + 1 /2 − 𝑖 √3 /2

par identification,

(1/ 2 + 𝑖 √3/2) z + 1 /2 − 𝑖 √3 /2 = ( −1/ 2 + i √3 /2 ) z - z_Ω(1+ ( −1/ 2 + i √3 /2 ))

1 /2 − 𝑖 √3 /2 = z_Ω(1/2+ i √3 /2 ))

=> z_{Ω = 1}

D'où, 𝑓 est la rotation de centre d'affixe 1 et d'angle 𝜋 /3

EXERCICE V :

1.On a: f(z)=2e^iπ/3 +3-i

La transformation F du plan associée à la bijection f est la composée d’une translation, d’une rotation de centre O et d’une homothétie de centre O :

avec

2.On peut écrire : f(z)=e^-iπ/4z -i

F est une rotation d’angle oriente de mesure -π/4

Désignons son centre par le point Ω d’affixe ω

On a : F(Ω)=Ω <=> f(ω)=ω

<=>Ѵ2/2(1-i)ω-i=ω =>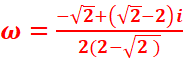

F est la rotation d’angle oriente de mesure -π/4 et de centre le point d’affixe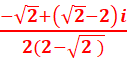

3.F est l’homothétie de rapport 2

Désignons son centre par le point Ω d’affixe ω.

On a : F(Ω)=Ω <=>f(ω)=ω

<=>2ω-3+i=ω =>ω=3-i

F est l’homothétie de rapport 2 et de centre le point d’affixe 3-i.

4. La bijection complexe f associée à h(Ω,-3) est définie par :

f(z)=-3z +b avec f(2+i)=2+i

d’ou -3(2+ i) + b=2+i =>b=4(2+i)

donc f(z)=-3z + 4(2+i).

5.La bijection complexe f associée à

r _(Ω,π/6) est définie par :

f(z)=e^iπ/6 z +b avec f(1-i)=1-i

d’ou f(1-i)= e^iπ/6(1-i) +b=1-i => b=(1-i)(1- e^{iπ/6 )}

donc f(z)= e^iπ/6 z +(1-i)(1- e^{iπ/6 )}

=1/2(Ѵ3+i)z +(1-Ѵ3)/2 – i(3-Ѵ3)/2

6.Soit z un nombre complexe.

On a : f₁(z)=e^iπ/4 z + b₁ et f₁(2i)=2i (1)

f₂(z)=-2z + b₂ et f2(-i)=-i (2)

f=f₂of₁ (3)

Des égalités (1) on obtient :

b₁=Ѵ2+(2-Ѵ2)i

Des égalités (2) on obtient:

b₂=-3i

Et de l’égalité (3) on obtient :

f(z)=-2e^iπ/4z -2Ѵ2+ (2Ѵ2-7)i .

Avez-vous un exercice à proposer ? Cliquez-ici

Merci de votre visite
Laissez un commentaire