LES ALGORITHMES
Plan du cours (cliquez sur un lien pour aller directement à la partie qui vous
intéresse)
GENERALITES SUR LES ALGORITHMES
I-GENERALITES SUR LES
ALGORITHMES
Un algorithme est une
suite d’actions ou d’instructions qui doivent être exécutées dans
un ordre bien déterminé pour résoudre un problème (ou réaliser un
travail) en un temps fini.
L'algorithmique
est l’ensemble des règles et des techniques qui sont impliquées dans la
définition et la conception d'algorithmes.
Si les instructions
d'un algorithme s’exécutent les unes après les autres, l'algorithme est dit séquentiel,
si elles s’exécutent en même temps, il est parallèle. Si l'algorithme
exploite des tâches s’exécutant sur un réseau de processeurs on parle d’algorithme
réparti, ou distribué.
STRUCTURE D‘UN ALGORITHME
|
Algorithme Nom_ Algorithme. Variables Entrée
Sortie.
Début Action1
Action2 Action n Fin |
← profil ←
variable d’entrée ←variable de sortie
← différentes actions ← délimiteur de fin |
1-Partie déclarative
1.1-Déclaration
des constantes
Une
constante est une donnée fixe qui ne
varie pas durant l’exécution d’un algorithme.
Une
constante est caractérisée par son nom et sa valeur (fixe).
Pour
déclarer une constante, on écrit le mot-clé const, suivi du nom de la constante et de sa valeur.
Syntaxe :
ConstNom _Constante = valeur ;
Exemples:
const Pi=3,14 ;
1.2-Déclaration
d’une variable
Une variable est un objet dont le contenu peut être modifié par une action
durant l’exécution d’un algorithme.
Une
variable est caractérisée par un identificateur qui est son nom, un
contenu qui est sa valeur et son type :
Exemple : age_du_visiteur =17.
Remarques :
1) Le nom
d’une variable doit commencer obligatoirement par une lettre. Il doit être
formé d’une ou de plusieurs lettres, les chiffres sont également autorisés.
Aucun espace ne doit figurer dans le nom d’une variable. Il vaut mieux
remplacer les espaces par la touche (underscore) « _ » du clavier.
De même, il est préférable que le nom donné à une variable soit évocateur de
l’information qu’elle contient.
2) On peut
modifier quand on veut la valeur d’une variable, faire des opérations dessus,
etc.
Pour
déclarer une variable, on écrit le mot-clé var, suivi du nom de la variable et
du type.
Syntaxe :
var
nom_de_la_variable : type ;
Exemples :
var age :
entier ;
var i,j,k :réels ;
Types de variables
·
Types numériques :
Les
types numériques les plus connus sont l’entier et le réel :
-Le
type entier (int) : ce
sont les nombres du type 1, 2, 3, 4, etc. On compte aussi parmi eux les nombres
relatifs : -1, -2, -3...
-Le
type réel :
Le
type réel recouvre un ensemble de nombres réels qui ne correspond pas toujours
aux réels en mathématiques. Il comprend les
nombres décimaux (float) qui sont
des nombres à virgule, comme 14,738. Le traitement et l’affichage des données
de ce type se font à virgule flottante, c’est à-dire qu’il est possible de les
écrire en déplaçant le point à volonté et en utilisant une puissance appropriée dans la base choisie.
Exemple : 235.67= 0.23567.103=23467.10-2
On note aussi 0.23567E3 ou 23467E-2.
·
Type booléen (bool) :
C'est
un type très important qui ne permet de stocker que deux valeurs, par
exemple vrai ou faux (on écrit true
pour vrai, et false pour faux).
Une
variable type booléen ne peut prendre que deux valeurs représentées par les
identificateurs Vrai ou Faux.
Exemple : 14>5 est Vrai
14<5 est Faux---sont des
expressions booléennes
·
Type caractère :
Il
appartient à l’une des catégories suivantes :
- Les chiffres de 0 à 9
- Les lettres de l’alphabet (de A à Z)
majuscules et minuscules.
- Les caractères spéciaux +,-,*,
/ ; etc. qui correspondent aux
touches du clavier, y compris les touches de fonction telles que la barre
d’espacement et la touche entrée.
Une
variable caractère occupe un octet en mémoire. A chaque caractère correspond un code
(appelé code ASCII) qui est un entier compris entre 0 et 255.
Remarques :
-Un caractère est généralement placé
entre 2 guillemets.
Exemple :
‘’ a ‘’ ; ‘’ g’’ ; ‘’ 128 ‘’.
-Un caractère vide est représenté par
deux paires de guillemets ‘’ ‘’
-Une variable de type caractère ne peut
contenir qu’un et un seul caractère
-Tous les caractères sont ordonnés selon
leur code ASCII variant de 0 à 255.
Type chaine de
caractères
Une
chaine de caractère est un
regroupement de plusieurs caractères. La chaîne de caractères est le nom
informatique qu'on donne au texte. On
peut stocker des textes courts comme de très longs textes au besoin.
Exemples:
·
"Je
suis un texte". Une chaîne de caractères est habituellement écrite entre
guillemets ou entre apostrophes (on parle de guillemets simples) : 'Je suis un
texte'. Les deux fonctionnent mais il ne faut pas les mélanger.
·
" bonjour "
Attention : 234 peut désigner le nombre deux cent trente- quatre comme
il peut désigner une suite de caractère 2, 3,4. Dans ce dernier cas, on écrit
entre guillemets ‘’ 234 ‘’ pour faire la différence.
2-Initialisation
Dans
cette partie, on attribue des valeurs initiales aux variables. Par exemple,
lorsqu’on veut calculer une somme S,
on affecte une valeur initiale à S
pour éviter que la case mémoire correspondante ne contienne des déchets des
programmes précédents.
3-Traitement
Dans cette
partie, On insère les instructions du programme qui concernent les traitements.
4-Edition
Ici, on
insère les instructions de sortie des résultats telles que l’affichage ou
l’impression des résultats.
Les commentaires
Les commentaires sont souvent
utilisés pour permettre une interprétation aisée de l’algorithme. On les place
entre/* et */ ou
(ou entre co et fco).
II :
INSTRUCTIONS
SIMPLES
1-Instruction
de lecture (ou opérations d’entrée des données)
L’instruction de lecture demande à
la machine de lire une valeur saisie par un utilisateur à partir du clavier ou
de lire une valeur contenue dans une
mémoire de stockage. Elle se réduit au verbe LIRE.
Syntaxe : Lire (variable) ;
Exemples : Lire (note) ;
Lire (A, B) ;
A et B étant des variables.
2-Instruction
d’écriture (ou opération de sortie des résultats)
L’instruction
d’écriture demande à la machine d’afficher le résultat d’un traitement à
l’écran. Elle se réduit au verbe ECRIRE.
Syntaxe : Ecrire(variable) ;
Ecrire (‘’ message’’, variable)
Exemples : Ecrire(Résultat) ;
Ecrire ('’Le résultat est :'’, Résultat) ;
3-Instruction
d’affectation
Cette instruction
permet de ranger une valeur
dans une variable. Elle se symbolise par
←.
Syntaxe : Variable ← valeur
Exemples : x ← 35 veut dire que x
prend la valeur 35.
A
←2 : la variable A
reçoit la valeur 2
B←A+1 : la variable B reçoit le contenu de A plus 1
Nom←'Mohamed' : la variable Nom reçoit la valeur Mohamed
Exemple :
1-Ecrire (« Entrer la valeur de
l’entier a :») ;
2- Lire (a) ; /* on saisit la valeur de l’entier a au
clavier */
3-Ecrire
(« Entrer la valeur de l’entier b : ») ;
4- Lire (b) ; /* on saisit la valeur de l’entier b au clavier
*/
4-S← a+b;
5-Ecrire (« La somme S
est : », S); /* On affiche le résultat à l’écran */
III- OPERATEURS ET
EXPRESSIONS
1-Opérateur
Un opérateur est un signe qui relie deux valeurs, pour produire un
résultat.
Les opérateurs possibles dépendent du type des
valeurs qui sont en jeu.
1.1- Opérateurs numériques
Ce sont les quatre
opérations arithmétiques et tout ce qu’il y a de classique.
+ : addition
- : soustraction
* : multiplication
/ : division
^ : qui signifie « puissance ».
45 au carré s’écrira donc 45 ^ 2.
DIV (A, B) : donne le
quotient de la division entière de A par B
MOD (A, B) : donne le reste
de la division entière de A par B
Exemples : A=5 et B=2
A/B=2.5
DIV(5,2)=2 ;
MOD(5,2)=1.
1.2-Operateurs
de comparaison
<strictement
inférieur > strictement supérieur
<=
inférieur ou égal >= supérieur ou égal
= égal
<> différent de
1.3- Opérateur
alphanumérique : &
Cet opérateur permet de
concaténer,
autrement dit d’agglomérer, deux chaînes de caractères.
Exemples
Variable : A ; B ; C en caractères
A← ‘’Michel’’
B← ‘’ Amougou’’
C← A &B
La valeur de C à la fin de l’algorithme est
"MichelAmougou"
1.4- Opérateurs logiques
Il s’agit du ET, du OU,
du NON
|
a |
b |
Non
a |
a
ET b |
A
OU b |
|
Vrai |
Vrai |
Faux |
Vrai |
Vrai |
|
Vrai |
Faux |
Faux |
Faux |
Vrai |
|
Faux |
Vrai |
Vrai |
Faux |
Vrai |
|
Faux |
Faux |
Vrai |
Faux |
Faux |
1.5-Opérateurs
de type booléen
Ils sont de la
forme :
-VRAI ou FAUX
-OUI ou NON
On obtient un résultat de type booléen quand on
est amené à comparer des expressions entre elles, au moyen des opérateurs de
comparaison.
2-Expression
Une expression est un ensemble de valeurs,
reliées par des opérateurs, et équivalent à une seule valeur. Par exemple,
voici quelques expressions de type numérique :
7
5+4
123-45+844
Toto-12+5-Riri
…sont toutes des expressions valides, pour peu
que Toto et Riri soient bien des nombres car dans le cas contraire, la
quatrième expression n’a pas de sens.
|
Expression |
Résultat |
|
20>4 |
Vrai |
|
12<=5 |
Faux |
|
30>5 et 5<3 |
Faux |
3-Priorité
des opérateurs
Pour les opérateurs
arithmétiques donnés ci-dessus, l’ordre de priorité est le suivant (du plus
prioritaire au moins prioritaire).
( ) : Les parenthèses.
^ : Élévation à la puissance
*,/ :multiplication, division.
+,- : addition, soustraction
En cas de besoin, on utilise les parenthèses pour indiquer les
opérations à effectuer en priorité. A priorité égale, l’évaluation de
l’expression se fait de la gauche vers la droite.
Exemples :
1+ (2*3)=7
1*(2+3)=5 /* les
parenthèses sont prioritaires */
1*2+3=5
1+2*3=7 /*
la multiplication est prioritaire sur l’addition */
3*3^2=27
3^3*2=54 /* la puissance est
prioritaire sur la multiplication */
1+3-2=2
1-3+2=0 /* à priorité
égale, l’évaluation se fait de la gauche vers la droite*/
On a le droit
d’utiliser les parenthèses, avec les mêmes règles qu’en mathématiques. La
multiplication et la division ont « naturellement » priorité sur
l’addition et la soustraction. Les parenthèses ne sont ainsi utiles que pour
modifier cette priorité naturelle.
Cela signifie qu’en informatique, 12 * 3 + 5 et
(12 * 3) + 5 valent strictement la même chose, à savoir 41
En revanche, 12 * (3 + 5) vaut 12 * 8 soit 96.
IV
: LES ALGORIGRAMMES
C’est la représentation graphique des algorithmes avec des
figures géométriques (rectangles, parallélogrammes, losanges, etc.). On les
appelle souvent logigramme, organigramme et rarement ordinogramme.
2-Symboles
|
Marque le début ou la fin d’un algorithme.
Marque les
instructions de lecture ou d’écriture
Marque une
action simple à exécuter.
Représente un
sous-programme
Marque une question posée par l’évaluation d’une condition
C qui a la valeur soit « vrai », soit « faux ». O Anneau numéroté
utilisé pour les algorithmes longs de plus d’une page. Il permet de repérer
la fin de la première page et le début de la seconde. |
|
![]()
Flèche de connexion
pour indiquer le sens de lecture
Exemple :

V-STRUCTURES DE CONTROLE
Les structures séquentielles (ou bloc d’actions)
La structure
séquentielle est une structure dont les instructions sont exécutées les unes
après les autres de façon à ce que l’ordre des instructions soit respecté.
Exemple : Algorithme qui permet
le calcul d’une somme
Organigramme :

Code :
Algorithme
Somme
Var a,
b, S : réels ;
Début
Ecrire (« Entrer le réel a : »), Lire (a) ;
Ecrire (« Entrer le réel b : »), Lire (b) ;
S ←
a+b ;
Ecrire (« La somme est : »,S) ;
Fin
LES STRUCTURES
CONDITIONNELLES (OU ALTERNATIVES)
1-Structure conditionnelle simple
Syntaxe :
SI condition ALORS
Traitements
. FinSI

Exemple
Un algorithme qui calcule le maximum de deux nombres
réels.
|
Algorithme Maximum |
2-Structure
conditionnelle complète (deux choix)
|
Syntaxe : SI condition ALORS // Traitements1 SINON // Traitemants2 FinSi |
|
Organigramme
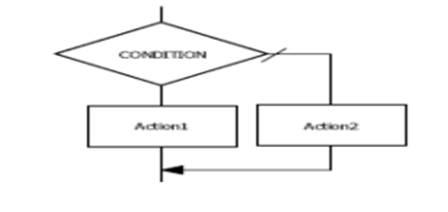
Exemple
Un algorithme qui demande un nombre entier à
l’utilisateur, et l’informe ensuite si ce nombre
est positif ou négatif
|
3-Structure alternative imbriquée
|
Syntaxe : Si condition1 Alors //Traitements1
Sinon Si condition 2 Alors // Traitements2
; Sinon // Traitements3
; Fin si Fin si |
|
|
Exemple : Etat de l’eau selon sa température
(glaçon, liquide, vapeur) SI la température de
l’eau est inférieure à 0° ALORS -
C’est la glace SINON SI La température de l’eau est
supérieure à 0 et inférieure à 100°
ALORS § C’est du liquide SINON -C’est la vapeur FinSi FinSi |
Code : Algorithme etatEau Variables A,
B : booléens ; Temp : réel ; Début Lire(Temp) ; A←Temp<=0 ; B←0<Temp<100 ; SI
A ALORS Ecrire (‘’C’est la
glace ‘’) ; SINON SI B ALORS Ecrire (’’ C’est le
liquide’’) ; SINON Ecrire (‘’ C’est la vapeur’’) ; FinSi FinSi Fin |
LES STRUCTURES ITERATIVES
On
utilise les schémas itératifs lorsqu’on veut exécuter une liste d’actions plusieurs
fois. Le nombre d’itérations peut être connu ou non. Dans certains cas, on
utilise certaines conditions pour contrôler le déroulement des
itérations ; on distingue entre autres :
·
La
structure itérative complète ou la structure POUR … FAIRE …
·
Les
structures répétitives à condition d’arrêt, composées de deux structures :
_ la structure REPETER … JUSQU’A …
_ la
structure TANT QUE … FAIRE …
Ainsi
quand on a à écrire une répétitive, on doit d’abord poser la question
suivante : est- ce qu’on connait le nombre d’itérations à faire dans la
boucle ? Après analyse si la réponse est affirmative on utilise ‘’ POUR ‘’ sinon on utilise ‘’TANT QUE’’ ou REPETER
Instruction
d’incrémentation/décrémentation.
L’incrémentation (tout
comme la décrémentation) est beaucoup rencontrée dans les structures à boucle. C'est-à-dire
dans les structures répétitives. En effet, on peut les assimiler à des
compteurs qui, à chaque cycle augmentent ou diminue de 1.Les variables les plus
impliquées à cette opération sont les variables de contrôle. On les représente
par :
i ← i+1
incrémentation veut dire ’’Ajouter 1 à la valeur actuelle de i’’.
j←
j-1 décrémentation veut dire
‘’Retrancher 1 à la valeur actuelle de j’’.
Attention : Il faut généralement initialiser i et j appelés souvent
compteurs. Exemple i=0
1-La
structure itérative complète (POUR...FAIRE)
Une structure
itérative est dite complète si le nombre de répétition est connu d’avance.
Cette structure est caractérisée par :
-l’initialisation automatique du compteur à une
valeur initiale Vi
-l’incrémentation/décrémentation du compteur à
chaque répétition
-vérification du compteur pour qu’il ne dépasse
pas la valeur finale Vf
Syntaxe :
POUR Cp deVi à Vf PAS de 1 FAIRE
Instruction 1
Instruction 2
….
Instruction n
FinPOUR
Cp ; compteur ;
Vi =Valeur initiale ;
Vf=Valeur finale
PAS= valeur de l’incrémentation
Organigramme :

Exemple : Calculer la somme des 9 premiers chiffres
|
Algorithme SommeEntiers Variable Somme : entiers ; Début Somme
← 0 ;
/* initialisation*/ POUR i=1 à 9 FAIRE Somme ← Somme +i ; i ← i + 1 FinPour ECRIRE (‘’ La somme est :’’,
Somme) ; Fin |
2-Les
structures itératives à condition d’arrêt
Une structure itérative est dite à condition d’arrêt si le
nombre d’itérations n’est pas connu d’avance, mais il dépend d’une condition.
2.1- La structure ‘’TANT QUE …FAIRE ‘’
Avec la structure « TANT
QUE », le nombre d’itérations n’est pas à priori connu : Soit c la
condition qui prend la valeur « VRAIE » ou « FAUSSE »,
chaque itération commence par l’évaluation de la condition. Une condition est
une comparaison. Elle est composée de 3 éléments : une valeur, un
opérateur de comparaison et une autre valeur :
-si la valeur de la condition est
vraie, alors on exécute la liste d’action. Les itérations se poursuivent
jusqu’à ce que la condition c deviennent fausse :
-si la valeur de la condition est
fausse, on n’exécute pas les actions de
tant que
Syntaxe :
TANT QUE condition(s) FAIRE
// Traitements
Fin
TANT QUE
Organigramme :

Exemple :
|
Algorithme
Application Var i,
n : entiers ; Début i←1 ; Tant que i<=10 faire Ecrire (« l’itération est exécutée ») ; i←i+1 FinTant que Fin |
2.2- La structure « REPETER…JUSQU'A »
La structure REPETER…JUSQU'A… est utilisée quand il s’agit de répéter un
traitement un nombre de fois inconnu à l’avance et qu’on est sûr que le
traitement itératif s’exécutera au moins une fois. Dès que la condition
d’arrêt devient vraie, la boucle est abandonnée et le programme continue en
séquence.
La structure
« REPETER » commence par l’exécution de la liste d’actions. On évalue
ensuite la condition :
- si la valeur est fausse, alors, on continue le
processus d’itérations
-si par contre,
après évaluation de la condition, on trouve qu’elle a pour valeur VRAIE, on
sort de la boucle.
Syntaxe :
REPETER
Instruction 1
Instruction 2
….
….
Instruction n
JUSQU'A condition(s) d’arrêt
Organigramme :

Exemple : Ecrire un algorithme
qui dit plusieurs fois « bonjour Monsieur ».
|
Algorithme
bonjour Var i :entier ; Début i←1 ; Répéter Ecrire
(« bonjour Monsieur») ; i←i+1 ; Jusqu’à i>10 Fin |
Propriétés
1- Quelle que soit la valeur initiale
des conditions, la liste d’action est exécutée au moins une fois
2- Il doit avoir au moins une action
qui met à jour la valeur de la condition.
STRUCTURES
DES DONNEES
Introduction
Une structure de données est une manière d’organiser les
données pour faciliter les traitements. On distingue plusieurs types de
structure de données :
-Les structures linéaires : les tableaux,
les listes, les piles et les files.
-Les structures non linéaires : les arbres
et les graphes.
Dans le cadre de ce cours, nous allons nous
limiter aux structures linéaires
I- TABLEAUX
1-Définition
Un tableau est un regroupement de valeurs
portant le même nom de variable qui sont repérées par un numéro. Il permet de
ranger un nombre fini d’éléments de même
type et selon une disposition bien définie.
Tableau NOTES
|
Indice |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Valeur |
8 |
12 |
11 |
5 |
16 |
13 |
7 |
14 |
12 |
4 |
17 |
Le numéro qui permet de repérer chaque valeur
s’appelle l’indice (ici les indices
vont de 0 à 10).
2-Accéder à
un élément d’un tableau
Chaque fois que l’on veut désigner un élément du tableau, on fait
figurer le nom du tableau, suivi de l’indice de l’élément, entre crochets.
On accède ainsi à la ième
valeur d’un tableau en utilisant la syntaxe suivante :
Nom_du_tableau
[indice] ;
Exemple : NOTES [6] /* donne la
valeur 7 * /
L’accès à un élément du tableau se fait par
l’intermédiaire de son indice qui représente l’emplacement de l’élément dans le
tableau : c’est l’accès direct.
On
peut parcourir les éléments d’un tableau à l’aide d’une boucle.
3- Déclaration
d’un tableau
La
formulation simple de la déclaration d’un tableau est la suivante :
Syntaxe :
Nom_tableau : tableau [indice
inférieure…indice supérieure] de type_de_données ;
OU
Nom_tableau : tableau[taille]detype_de_données ;
Exemple : Pour un tableau de 30
notes des élèves d’une classe, on note :
Si Notes est le nom du tableau, on
écrit :
Notes : Tableau [1…30] de réelOU Notes :
Tableau [30] de réels
1-Saisie des
éléments d’un tableau
Si tab
est un tableau de 10 entiers
tab
[2] ←5 met la valeur 5 dans la deuxième case du tableau
En considérant le cas où a est une variable de
type entier, a←tab[2] met la valeur de la deuxième case du tableau dans a
c.-à-d. 5.
Pour
saisir les variables d’un tableau données par un utilisateur, on utilise la
syntaxe suivante
Syntaxe :
Lire
(tab[i]) ;
On peut utiliser une boucle
Exemple :
|
Algorithme SaisieNotes var tab : Tableau [1…N] de réels var N, i : entiers ; Début Pour i de 1 à NFaire Lire (tab[i]) ; FinPour FinSaisieNotes |
2-Afficher
les éléments d’un tableau
Syntaxe :
Afficher(T[i]) ;
Exemple :
|
AlgorithmeAfficherNotes var tab : Tableau [1…N] de réels ; var N,i : entiers ; Début Pour i de 1 à N Faire Afficher (tab[i]) ; FinPour FinAfficherNotes |
3-Recherche
dans un tableau
La
recherche séquentielle ou recherche linéaire est un algorithme pour trouver une
valeur dans une liste. L’accès dans une liste est dit séquentiel lorsqu’on
passe en revue tous les éléments de la liste pour avoir accès à l’élément
recherché.
3.1-Recherche l’élément minimum d’un tableau.
On suppose que le tableau est déjà saisi.
Exemple :
|
Algorithme RechercheMinTableau const n=10 ; tab : Tableau [1…N] de réels varN, i : entier ; varMin : entier ; Début Pour i de 1 à NFaire
Si tab[i] < Min alors
FinSi FinPour Afficher (Min) ; FinRechercheMinTableau |
3.2-Recherche séquentielle d’un entier x dans un
tableau
|
AlgorithmeRecherche_Nombre const n=10 ; var i : Entier ; var NombrCherch : Réel ; var Trouve : Booléen ; tab : Tableau [1..n] de Réel ; Début //Remplissage du tableau Pour i allant de 0 à 9 faire Ecrire (" entrer les notes ") ; Lire tab[i]) ; FinPour Écrire (‘’entrez la note que vous recherchez’’) ; Lire (NombrCherch) ; i ← 1 ; Trouve ←0 ; Tantque(i<=n) et
(Trouve=0)Faire Si tab[i]=NombrCherch alors Trouve ←1 ; Sinon i ← i+1 ; FinSi FinTantque Si (Trouve=1)alors Ecrire(" La note recherchée se trouve à
l’indice ", i ) ; Sinon Ecrire(" ECHEC " ; FinSi FinAlgo |
La recherche dichotomique
Cette
méthode est rapide car on ne consulte pas séquentiellement tous les éléments du
tableau.On s’appuie sur le fait que le tableau soit trié pour, au cours des
itérations, évaluer avec de plus en plus de précision l’endroit où se trouve
l’élément cherché.
La dichotomie,
c’est le fait de couper en deux le tableau trié et de regarder dans quelle
partie du tableau se trouve l’élément cherché.On recoupe en deux cette partie
du tableau et on regarde à nouveau dans quelle moitié l’élément peut se
trouver.
5-Exécution
pas à pas d’un algorithme de Tri par insertion
On
parcourt le tableau du début à la fin, et à l’étape i on considère que les
éléments de 0 à i-1 du tableau sont déjà triés. On va alors placer le ième
élément à sa bonne place parmi les éléments précédents du tableau, en le
faisant descendre jusqu’à atteindre un élément qui lui est inférieur.
Exemple :
|
AlgorithmeTri_Par_Insertion tab : Tableau [1…N] de réels ; Aux :
Entier ; N :
Entier ; DEBUT Pour jde 2 àN Faire Aux ← tab[ j ] ; i←
j-1 Tant Que i >0 et tab [ i ] >Aux Faire tab
[i+1] ←tab[i] ; i← i -1 ; FinTantQue tab[i + 1] ← Aux ; Fin Pour FinTri_Par_Insertion |
Trace
d’exécution :
On suppose que le tableau est déjà créé :27
10 12 8 11
|
N° ligne |
var1 |
Var2 |
Instructions |
Ecran |
|
|
j=2 |
i=1 |
Aux=10 i>0 et
tab[1]=27 >12 VRAI, on entre dans
la boucletab[2]=27 |
27 27 12 8
11 |
|
|
|
i=0 |
i>0 FAUX,
on n’entre pas dans la boucle tab[1]=10 |
10 27 12 8
11 |
|
|
j=3 |
i=2 |
Aux=12,i>0
et tab[2]=27>12 VRAI , on entre
dans la boucle tab[3]=27 |
10 27 27 8
11 |
|
|
|
i=1 |
i>0 et
tab[1]=10 >10 FAUX, on n’entre
pas dans la boucle tab[2]=12 |
10 12 27 8
11 |
|
|
j=4 |
i=3 |
Aux=8
,i>0 et tab[3]=27>8 VRAI, on
entre dans la boucle tab[4]=27 |
10 12 27
27 11 |
|
|
|
i=2 |
i>0 et
tab[2]=12>8 VRAI, on entre dans la boucle tab[3]=12 |
10 12 12
27 11 |
|
|
|
i=1 |
i>0 et
tab[1]=10>8 VRAI, on entre dans la
boucle tab[2]=10 |
10 10 12
27 11 |
|
|
|
i=0 |
i>0
FAUX, on n’entre pas dans la boucle tab[1]=8 |
8 10 12 27 11 |
|
|
j=5 |
i=4 |
Aux=11,i>0
et tab[4]=27>11 VRAI, on entre dans la boucle tab[5]=27 |
8 10 12 27 27 |
|
|
|
i=3 |
i>0 et
tab[3]=12>11 VRAI, on entre dans la
boucle tab[4]=12 |
8 10 12 12 27 |
|
|
|
i=2 |
i>0 et
tab[2]=10>11 FAUX, on n’entre
pas dans la boucle tab[3]=11 |
8 10 11 12 27 |
II-ENREGISTREMENTS
1-Définitions
Un enregistrement est un
type de données défini par l’utilisateur qui permet de regrouper un nombre fini
d’éléments de types éventuellement différents sous un nom commun.
Les éléments qui
composent un enregistrement sont appelés champs.
A la différence des tableaux, qui ne permettent que les éléments du même type,
les enregistrements permettent de combiner différents types de données.
Pour créer des
enregistrements, il faut déclarer un nouveau type dit type structuré, basé sur d’autres types existants. Ce nouveau type
peut être utilisé comme un type normal en déclarant une ou plusieurs variables
de ce type.
2-
Déclaration d’un type structuré
Avant de déclarer une
variable enregistrement, il faut avoir au préalable définir son type, c-à-d le
nom et le type de champs qui le composent.
Syntaxe :
Type
Nom_Type=Enregistrement
Champ1 : Type 1
Champ2 : Type 2
….
Champ N : Type N
FinNom_type
Exemple :
|
Type Personne : Enregistrement Nom : chaine Prenom : chaine Age : Entier FinPersonne |
3-Définition d’une
variable de type structuré
Une
fois qu’on a défini un type structuré, on peut déclarer des variables
enregistrements exactement de la même façon que l’on déclare des variables d’un
type primitif :
Syntaxe :
var nom_variable : nom_enregistrement ;
Exemple : Déclaration de deux
variables pers1 et pers2 de type Personne
pers1, pers2 : Personne
1-Accès à un
champ d’un enregistrement
Alors que les éléments d’un tableau sont accessibles à
travers leur indice, les champs d’un enregistrement sont accessibles à travers
l’opérateur de champ qui est un simple point «.»
Syntaxe :
Nom_variable.Nom_champ
Exemple :
Pour accéder à l’âge de la variable pers2, on
écrit tout simplementpers2.age
2-Affectation
L’affectation de
valeurs aux différents champs d’une variable enregistrement se fait comme
suit :
Syntaxe : variable.champ ←valeur ;
Exemple : pers1.Nom← « Fati »
3-Lecture
Syntaxe :Lire(variable.champ) ;
4-Ecriture
Syntaxe : Ecrire (variable.champ) ;
Exemple :Soit un algorithme qui
saisit des données des élèves E1 et E2 et calcule la différence de leurs notes.
|
AlgorithmeRelevéNotes Type Fiche=Enregistrement Nom,prenom :chaine Sexe : caractere Date_naissance :chaine Note : réel FinEnregistrement Var E1,E2 :Fiche Début Afficher(" Entrer les données de E1 ") ; Ecrire (E1.nom,E1.note) ; Afficher(" Entrer les données de E2 ") ; Ecrire(E2.nom, E2.note) ; Afficher(" La difference des des notes ") Si E1.note >E2.note alors Afficher(" la difference des note est ", E1.note-E2.note ; Sinon Afficher (" la difference des notes est : ", E2.note-E1.note) ; FinSi FinAlgo |
Remarques :
1- Il n’existe pas de constante type
enregistrement.
2-Les seules opérations sur les enregistrements
sont l’affectation et le passage comme paramètre.
3-Les seules expressions d’un type
enregistrement sont les variables de ce type.
4-Il n’y a pas de fonction (même prédéfinie) à
résultat d’un type enregistrement.
III-LES LISTES
1-Limites des tableaux
·
Les
données présentes dans un tableau sont contigües c.-à-d. côte-à-côte dans la
mémoire, ce quientraine que la taille du tableau est fixe.
·
On
ne peut ni ajouter une case à la fin d’un tableau, ni insérer une case au
milieu (sauf pour les tableaux dynamiques)
2-liste
2.1-Définitions
·
Une
liste est une structure de données permettant de regrouper des données de
manière à y accéder librement.
·
Une
liste chainée est une structure de données représentant une collection ordonnée
et de taille arbitraire d’éléments de même type de base, dont la représentation
en mémoire de l’ordinateur est une succession de cellules faites d’un contenu
et d’un pointeur vers une autre cellule.
Techniquement,
une case (cellule) contient :
·
La
valeur de la case
·
L’adresse
de la case suivante (qui n’est pas forcement voisine) : c’est le pointeur.
On dit
que la cellule n° 1 pointe vers la cellule suivante qui se trouve à l’adresse
2000 (et non 2).
Une liste chainée est
constituée de plusieurs maillons. On peut ajouter des maillons au début, à la
fin de la liste ou insérer un maillon à l’intérieur d’une liste (ce qui n’est
pas possible dans un tableau qui n’est qu’une liste simple).
Un maillon aura la
structure suivante.
STRUCTURE maillon
{
Elément : type ;
Suivant : ^Suivant ; /* pointeur vers le maillon
suivant
}
2.2-Types de listes chainées
Il existe plusieurs
types de listes chainées :
-Liste simplement chainée
-Liste doublement chainée
2.2.1-Liste simplement chainée
Dans une liste
simplement chainée, chaque élément dispose d’un pointeur sur l’élément suivant
(ou successeur) de la liste. Le parcours se fait dans un seul sens.
Schéma :
Voici une
représentation possible :

Dans ce schéma, on n’a
pas besoin que les cellules soient contigües comme dans le cas des tableaux.
Contrairement aux tableaux, les listes chainées n’ont pas de taille fixe autre
que celle de la mémoire disponible. Chaque élément dispose d’un pointeur vers
l’élément suivant (ou successeur) de la liste. Le parcours se fait dans un seul
sens, ici l’accès se fait de manière
séquentielle : chaque élément permet l’accès à l’élément suivant
(contrairement aux tableaux par lequel l’accès se fait de manière directe, par
adressage de chaque cellule du tableau.)
Une
liste chainée est caractérisée par un pointeur tête(ou premier) vers le premier
élément et un pointeur queue (ou dernier) vers le dernier de la liste. A la fin
de la liste, on pointe sur une adresse in valide NULL. Cependant on peut aussi
pointer le dernier élément sur le premier, la liste devient alors cyclique.
STRUCTURE liste
{
Tête : ^maillon ;
Queue : ^maillon ;
}
2.2.2-Fonctions
utilisées dans les listes
·
Initialisation
·
Ajout
d’un élément
·
Suppression
·
Accès
à l’élément suivant
·
Accès
aux données utilisateurs
·
Accès
au premier élément de la liste
·
Accès
au dernier élément de la liste
·
Calcul
de la taille de la liste
·
Suppression
de la liste entière
Le principal problème des listes simplement chainées est
l’absence du pointeur sur l’élément précédent du maillon, il est donc possible
de parcourir la chaine uniquement du début vers la fin.
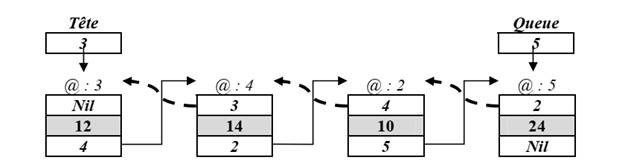
2.2.3- Liste doublement chainée
A la différence des
listes simplement chainées, les maillons d’une liste doublement chainée
possèdent deux pointeurs, respectivement sur l’élément suivant (ou successeur)
et sur l’élément précédent (ou prédécesseur). Le sens de parcours peut se faire
dans les deux sens mutuellement opposés.
STRUCTURE liste
{
Premier : entier ;
Dernier : entier ;
}
IV-PILES
1-Définition
Une pile est une structure des données dans laquelle les
éléments entrent et sortent par un seul endroit appelésommet de la pile.
Les piles peuvent être
représentées comme une pile d’assiettes :
-on peut ajouter des assiettes au sommet de la
pile
-lorsqu’on veut enlever une, il s’agit de la
dernière ajoutée. On parle de structure LIFO (Last In First Out) en français
dernier entré Premier sorti.
Les piles ne sont que
des cas particuliers des listes chainées dont les éléments ne peuvent être
ajoutés et supprimésqu’au sommet de la liste (dernier).
De
ce fait la manipulation s’en trouve grandement simplifiée puisqu’elle ne
nécessite que deux fonctions :
-une fonction pour ajouter (empiler) un élément au sommet de la
pile.
-une seconde pour le retirer (dépiler)
![]()
![]()
![]()
![]() Empiler Dépiler
Empiler Dépiler
|
|
|
|
|
|
|
|
2-Les
procédures les plus utilisées dans les piles
·
Initialiser
(p) : initialisation d’une pile
·
Est_vide(p) :
vérification qu’une pile est vide
·
Taille :
taille d’une pile
·
Sommet(p) :
sommet de la pile
·
Dépiler(p) :
supprimer un élément de la pile
3-Rôles
Les
piles servent à revenir à l’état précédent et sont utilisées pour :
-implanter les appels de procédures (pour
revenir à l’état d’avant l’appel)
-Annuler une commande (Ctrl-Z de Word)
-Evaluer les expressions arithmétiques etc.
Remarques :
1-Sommet de la pile représente le dernier
élément de la liste.
2-Le premier élément de la pile ici dans ce cas
particulier est toujours égal à 1 e donc le champ premier de la structure n’est
plus nécessaire. La structure d’une pile représentée par un tableau sera
simplifiée.
V-FILES
1-Définition
Une file est une liste chainée d’information dans
laquelle :
-Un élément ne peut être ajouté qu’à la queue
de la file
-Un élément ne peut être retiré qu’à la tête de
la file, Comme pour une file d’attente.
Les
files sont aussi appelées structures FIFO (First In First Out) en français
Premier entré Premier sorti.
![]()
![]()
![]() Tête Queue
Tête Queue
![]()
2-Fonctions
utilisées dans les files
Les
procédures les plus utilisées dans les files sont :
·
Initialiser
·
Est_vide
·
Taille
·
Tête
·
Queue
·
Défiler
La fonction initialiser(p) permet de réutiliser
la pile (pas d’initialisation du tableau)
La fonction est_vide
prend la valeur vraie si la file est vide
3-Rôle
Les files servent à traiter
les données dans l’ordre où elle les a reçues. Elles permettent de :
-gérer les processus en attente d’une ressource
système (par exemple la liste des travaux à éditer sur une imprimante)
-construire les systèmes de réservation etc.
EXERCICES
CONTROLE DE CONNAISSANCES
1 : Définir : structure de données, tableau.
2 : Quelles sont les limites d’un tableau ?
3 : Cite 04 structures de données linéaires.
4 : Cite 04 structures de données non linéaires.
5 : Citer 03 structures de contrôle.
EXERCICE I. Soit
l’algorithme ci-dessous :
1. Algorithme CalculNotes
2. Notes : Tableau
[1…5] de réels ;
3. Var i, s : entiers ;
4. Début
5. S ← 0 ;
6. Pour i de 1 à 5 Faire
7 .Ecrire (« Entrer
une note») ;
8 .Lire Notes [i] ;
9. FinPour
10 .
11. Pour i de 0 à 5 Faire
12. S ← S
+Notes[i];
13. FinPour
14. Ecrire (« Moyenne : », S/5) ;
15.Fin
Questions :
1. Définir : variable.
2. Identifier 02 variables dans cet
algorithme, préciser leur type.
3. Que font les lignes n°2 et n°5 de cet
algorithme ?
4. Identifier les parties de cet
algorithme.
5. Identifier 01 instruction de lecture,
01 instruction d’écriture et 01 instruction d’affectation.
6. Comment se fait l’accès à un élément
quelconque d’un tableau.
EXERCICES II : Soit l’algorithme
ci-dessous :
1. Algorithme
2. N : tableau
[6] d’entiers ;
3. Var i, k : entiers ;
4.Début
5. N [0] ← 1 ;
6. Pour k de 1 à 6 Faire
7. N[k] ← N (k-1) + 2 ;
8. FinPour
9. Pour i de 1à 6 Faire
10. Ecrire N[i];
11 .FinPour
12.Fin
Questions
1. Identifier dans l’algorithme ci-dessus une structure de
contrôle.
2. Quelle est la différence entre une structure itérative complète
et une structure itérative à condition d’arrêt ?
3. Récrire les lignes 6, 7,8 en utilisant une structure itérative
à condition d’arrêt.
4. Quelle est la différence entre une structure Tant que…..faire et Répéter…Jusqu’à
5. Donner la trace d’exécution de cet
algorithme.
EXERCICE III : Soit l’algorithme
ci-dessous :
1.Algorithme
2. tab : tableau
[7] en entier
3. Variable i : entier ;
4.Début
5. tab [0] ←1 ;
6. tab [1] ← 1 ;
7 .Pour i de 2 à 7 Faire
8. tab[i] ←tab
[i-1] + tab [i-2] ;
9. FinPour
10. Pour i de 0 à 7 faire
11. Ecrire tab[i] ;
12. FinPour
13.Fin
Questions :
1-
Combien d’instructions compte cet algorithme ?
2-
Donner la trace d’exécution de cet algorithme
3-
Que fait cet algorithme ?
EXERCICE IV : Soit l’algorithme ci-dessous :
1.
Algorithme Recherche_Nombre
2 const n=5 ;
3. var i : Entier ;
4. NombrCherch : Réel ;
5. Trouve : Booléen ;
6. Notes : Tableau [1…n] de Réel ;
7. Début
8. Pour i allant de 0
à 5 faire
9. Ecrire (« entrer les notes ») ;
10. Lire (Notes[i]) ;
11. FinPour
12. Écrire (‘’entrez la note que vous
recherchez’’) ;
13. Lire (NombrCherch) ;
14. i ←
1 ;
15. Trouve ←0 ;
16. Tant que (i<=n ET Trouve==0) Faire
17. Si (Notes[i]==NombrCherch)
alors
18. Trouve ←1 ;
19. Sinon
20. i ← i+1 ;
21 FinSi
22. FinTant que
23. Si (Trouve==1) alors
24. Ecrire (« La note recherchée se trouve à l’indice »,
i ) ;
25. Sinon
26. Ecrire (« ECHEC » ;
27. FinSi
28.FinAlgo
Question :
1. Quel est le type
de la variable Trouve ?
2. Nommer
le type de recherche présentée par l’algorithme ci-dessus.
3. Indiquer
un autre type de recherche
4. Que
font les lignes de 8 à11 ?
5.
Exécuter manuellement cet algorithme avec le tableau :18 12 08 10 16
La note
cherchée étant 08
EXERCICE V : Soit l’algorithme ci-dessous :
1. Algorithme Tri
2. tab :
Tableau [1…N] de réels ;
3. Aux,
N : Entiers ;
4. Début
5. Pour j de 2 à N Faire
6. Aux ←
tab[j] ; N=5 ;
7 .i ←
j-1
8. Tant Que i >0 et tab [i]
>Aux Faire
9. tab [i+1] ←tab[i] ;
10. i ←
i -1 ;
11. FinTantQue
12. tab
[i + 1] ← Aux ;
13. Afficher
tab[i] ;
14. Fin Pour
15. FinTri
Questions
1.
Nommer le type de tri présenté par cet algorithme.
2.
Donner le principe d’un tri par insertion.
3.
Citer 02 autres types de tri.
4.Donner
la table d’exécution de cet algorithme pour le tableau : 27 10 12 8 11
EXERCICE VI: Soit
l’algorithme ci-dessous :
1. Algorithme
2. Type
3.
Personne=Enregistrement
4.
nom : chaine ;
5. . âge : entier ;
6. Fin Personne
7. Var pers1, pers2 : Personne ;
8. Début
9. Ecrire (« Entrer
l’âge de la première personne ») ;
10. Lire
(pers1.age) ;
10. Ecrire («Entrer l’âge de
la deuxième personne ») ;
11. Lire
(pers2.age) ;
12. Si pers1.age>pers2.age
alors
13. Ecrire
(« La différence d’âge est : », pers1.age -
pers2.age) ;
14. Sinon
15. Ecrire
(« La différence d’âge est plutôt », pers2.age - pers1.age) ;
16. FinSi
17. FinAlgo
Questions :
1-Définir : enregistrement.
2-
Identifier la déclaration d’un
enregistrement.
3-
Que représente pers1 et pers2 dans cet algorithme?
4-
Quelle est la différence entre l’accès à un champ d’un enregistrement et l’accès à un élément d’un tableau ?
5-Affecter
aux différents champs de cet enregistrement les valeurs : Fati, 20 ans.
EXERCICE VII : On vous
propose l’algorithme suivant :
1.
Algorithme
2. Type
3. Elément :
Enregistrement
4. symbole :
chaine de caractère
5. Z : entier
6. FinElément
7. var elt1, elt2, elt3 : Elément ;
8. var i : entier ;
9. var group : Tableau [1…3] de
Eléments ;
10.
Début
11.
Ecrire (‘’saisie des enregistrements’’) ;
12. elt1.symbole
← ‘’Na’’ ;
13. elt1.Z. ← 10 ;
14. elt2.symbole
← ‘’ Cl‘’ ;
15. elt2.Z. ←17 ;
16. elt3.symbole
← ‘’C’’ ;
17. elt3.Z. ← 6 ;
18. Ecrire
(‘’affichage des
enregistrements’’) ;
28. Pour i allant de 1 à 3 Faire
19. Ecrire (‘’
group[i].symbole’’) ;
20. Ecrire (‘’
group[i].Z’’) ;
21. FinPour
22. Fin
Questions
1- Que fait
la ligne 9 de cet algorithme ?
2-Quel est
le rôle de l’opérateur ‘’. ‘’?
3-Que fait
cet algorithme ?
EXERCICE VIII :
1-Ecrire un
algorithme qui déclare et remplit un tableau de 7 valeurs numériques en les
mettant tous à zéro.
2-Ecrire un
algorithme qui remplit un tableau avec 6 valeurs : 0, 1, 4, 9, 16,25. Il
les affiche ensuite à l’écran.
EXERCICE IX : Un annuaire téléphonique est
constitué d’un nom, d’un numéro de téléphone et d’une adresse.
1-Créez un
enregistrement représentant un annuaire téléphonique.
2-Comment
peut-on accéder à une adresse.
EXERCICE X :
Un
nombre complexe s’écrit sous la forme z=a+ib où a est la partie réelle
(P_réelle) et ib la partie imaginaire, a et b sont des réels.
1-Créer un
enregistrement nommé Complexe
2-Déclarer
une variable z’ de type Complexe.
CORRIGES
CONTROLE DE CONNAISSANCES
1- Une structure de données
est une manière d’organiser les données pour faciliter les traitements.
-Un tableau est un regroupement de valeurs
portant le même nom de variable qui sont repérées par un numéro. Il permet de
ranger un nombre fini d’éléments de même
type et selon une disposition bien définie.
2 -Limites des tableaux :
-les données sont du même type, on ne peut
pas utiliser les entiers et les caractères dans un même tableau.
-Les
données présentes dans un tableau sont contigües c.-à-d. côte-à-côte dans la
mémoire, ce qui entraine que la taille du tableau est fixe.
-On ne peut ni ajouter une case à la fin d’un tableau, ni insérer une
case au milieu.
3 : Tableau, enregistrement, listes chainées, piles,
files.
4 : Graphes, arbres
EXERCICE I.
1-Une variable est un objet qui peut
être modifié par une action au cours de l’exécution d’un algorithme.
2-i et s sont des variables de type
entier.
3-la ligne n°2 déclare un tableau.
-la ligne n°5 initialise la variable S à 0.
4-Entête : ligne1
Déclaration des variables : ligne 2
et 3
Délimiteur de début : ligne 4
Corps de l’algorithme : lignes 5….14
Délimiteur de fin : ligne 15
5-instruction de lecture : Lire
Notes(i) ;
-instruction d’écriture : Ecrire (« Moyenne : », S/9) ;
-instruction affectation: S ← S +Notes[i];
5-
L’accès à un élément du tableau se fait par l’intermédiaire de son indice qui
représente l’emplacement de l’élément dans le tableau : c’est l’accès direct.
NB : On
parle d’accès séquentiel lorsque
pour accéder à un élément donné, il faut parcourir tous les éléments précédents
comme une bande magnétique.
EXERCICES II :
1-Structure itérative complète :
lignes 6 à 8 Ou lignes 9 à 11.
2- Une structure itérative est dite complète si le nombre de
répétition est connu d’avance alors qu’une structure itérative à condition
d’arrêt a besoin d’une condition pour connaître la fin des itérations
3- k=1
Tant que (k<7) faire
N[k] ← N (k-1) + 2 ;
k←k+1 ;
Fin Tant
que
4-Pour la structure Tant que la
condition est au début donc on peut ne pas exécuter une seule action alors que
pour la structure Répéter …jusqu’à on exécute la boucle au moins une
fois.
5-
|
Ligne |
i |
k |
Instructions |
écran |
|
4 |
|
|
N[0]=1 |
|
|
7 |
|
1 |
N[1]=1+2=3 |
|
|
7 |
|
2 |
N[2]=3+2=5 |
|
|
7 |
|
3 |
N[3]=5+2=7 |
|
|
7 |
|
4 |
N[4]=7+2=9 |
|
|
7 |
|
5 |
N[5]=9+2=11 |
|
|
7 |
|
6 |
N[6]=11+3=13 |
|
|
10 |
|
|
|
3
5 7 9
11 13 |
6-Cet algorithme calcule et affiche les nombres impairs de 1 jusqu’à
13
EXERCICE III :
1-04 instructions.
2-
|
Ligne |
i |
Instructions |
écran |
|
5 6 |
|
tab [0] =1 ; |
|
|
8 |
2 |
tab [2] =1+1=2 |
|
|
8 |
3 |
tab [3] =2+1=3 |
|
|
8 |
4 |
tab [4] =3+2=5 |
|
|
8 |
5 |
tab [5] =5+3=8 |
|
|
8 |
6 |
tab [6] =8+5=13 |
|
|
8 |
7 |
tab [7] =13+8=21 |
|
|
10 |
0 à 7 |
|
1 1 2 5 8 13 21 |
3-cet algorithme calcule et affiche
la liste : 1 1 2 5 8 13 21
EXERCICE IV :
1. Trouve
est une variable de type booléen jouant le rôle de drapeau.
2. Recherche
séquentielle
3. Recherche
dichotomique
NB : La dichotomie,
c’est le fait de couper en deux le tableau trié et de regarder dans quelle
partie du tableau se trouve l’élément cherché. On recoupe en deux cette partie
du tableau et on regarde à nouveau dans quelle moitié l’élément peut se
trouver.
4. C’est le remplissage du tableau
5. n=5 nombreCherch=08
|
Ligne |
i |
Instructions |
écran |
|
|
|
n=5 trouve=0 |
|
|
16 |
0 |
I<5 ?vrai on entre dans la boucle
Tant que… |
|
|
23 |
1 |
Notes [1]=08 ?faux on saute la boucle
Si… I prend la valeur 2 |
|
|
|
2 |
Notes [2]=08 ? faux on saute la
boucle Si… I prend la valeur 3 |
|
|
|
3 |
Notes [3]=08 ? Vrai on entre dans la
boucle Si… |
|
|
18 |
|
Trouve prend la valeur 1 |
|
|
23 |
|
On entre dans la deuxième boucle Si… |
|
|
24 |
|
|
La note cherchée se trouve à l’indice 3 |
|
|
|
|
|
EXERCICE V:
1. Tri par insertion
2. Le tri par insertion considère
chaque élément du tableau et l’insère à la bonne place parmi les éléments déjà
triés. Ainsi, au moment où on considère un élément, les éléments qui lui e
précèdent sont déjà triés tandis que les éléments qui le suivent ne sont pas encore triés.
3.tri par
sélection, tri a bulle
4.Trace
d’exécution :
On suppose que le tableau est déjà
créé :27 10
12 8 11
|
N° ligne |
var1 |
Var2 |
Instructions |
Ecran |
|
|
j=2 |
i=1 |
Aux=10 i>0 et tab[1]=27 >12 VRAI,
on entre dans la boucle tab[2]=27 02 |
27 27 12 8 11 |
|
|
i=0 |
i>0 FAUX, on n’entre pas dans la boucle tab[1]=10 |
10 27 12 8 11 |
|
|
|
j=3 |
i=2 |
Aux=12,i>0 et tab[2]=27>12
VRAI , on entre dans la boucle tab[3]=27 |
10 27 27 8 11 |
|
|
|
i=1 |
i>0 et tab[1]=10 >10 FAUX,
on n’entre pas dans la boucle tab[2]=12 |
10 12 27 8 11 |
|
|
j=4 |
i=3 |
Aux=8 ,i>0 et tab[3]=27>8
VRAI, on entre dans la boucle tab[4]=27 |
10 12 27 27 11 |
|
|
|
i=2 |
i>0 et tab[2]=12>8 VRAI, on entre dans la boucle tab[3]=12 |
10 12 12 27 11 |
|
|
|
i=1 |
i>0 et tab[1]=10>8 VRAI, on
entre dans la boucle tab[2]=10 |
10 10 12 27 11 |
|
|
|
i=0 |
i>0 FAUX, on n’entre pas dans la boucle tab[1]=8 |
8 10 12 27 11 |
|
|
j=5 |
i=4 |
Aux=11,i>0 et tab[4]=27>11 VRAI, on entre dans la boucle tab[5]=27 |
8 10 12 27 27 |
|
|
|
i=3 |
i>0 et tab[3]=12>11 VRAI, on
entre dans la boucle tab[4]=12 |
8 10 12 12 27 |
|
|
|
i=2 |
i>0 et tab[2]=10>11 FAUX, on
n’entre pas dans la boucle tab[3]=11 |
8 10 11 12 27 |
EXERCICE VI:
1- Un enregistrement est
un type de données défini par l’utilisateur qui permet de regrouper un nombre
fini d’éléments de types éventuellement différents sous un nom commun.
2- Lignes 2 à 7
3- pers1 et pers2 sont des variables d’enregistrement.
4- L’accès à un champ d’enregistrement se fait à l’aide de l’opérateur’’ .’’ alors
que l’accès à un élément d’un tableau est l’accès direct
5- pers1.nom ←
‘’Fati’’
pers1.age
← 20
EXERCICE VII :
1-
La ligne 9 déclare un tableau d’enregistrement.
2-
L’opérateur ‘’. ‘’ permet
l’accès à un élément d’un enregistrement.
3-Saisit
et affiche deux caractéristiques d’un élément chimique.
EXERCICE VIII :
1- Algorithme InitialiseTableau
tab :
Tableau [0…7] de réels ;
var i
entier ;
Début
Pour i de 0 à 7 Faire
tab[i] ←
0 ;
FinPour
Pour i de 0 à 7 Faire
Afficher tab[i] ;
FinPour
Fin
2- Algorithme
AfficheTableau
T :
Tableau [5] d’entiers ;
var i :
entier ;
Début
Pour i de 0 à 5 Faire
T[i] ← i*i ;
FinPour
Pour i de 0 à 5 Faire
Ecrire
T[i] ;
FinPour
Fin
EXERCICE IX :
.
1- Type
Annuaire=Enregistrement
Nom :
chaine
Num_téléphone:
entier
Adresse :
chaine
FinAnnuaire
2-var pers1, pers2 : Annuaire
Pers1.nom
Pers1.adresse,
Pers1.num_téléphone
EXERCICE X:
1-
Type Complexe=Enregistrement
P_réelle :réel ;
P_imaginaire :réel ;
Fin Complexe
2-
Z’ : Complexe ;


