STRUCTURES DE CONTROLE

LES STRUCTURES SEQUENTIELLES (ou bloc d’actions)

La structure séquentielle est une structure dont les instructions sont exécutées les unes après les autres de façon à ce que l’ordre des instructions soit respecté.

Exemple : Algorithme qui permet le calcul d’une somme

Organigramme :

Code :

Algorithme Somme

Var a, b, S : réels ;

Début

Ecrire (« Entrer le réel a : »), Lire (a) ;

Ecrire (« Entrer le réel b : »), Lire (b) ;

S ← a+b ;

Ecrire (« La somme est : »,S) ;

Fin

LES STRUCTURES CONDITIONNELLES (ou alternatives)

Structure conditionnelle simple

Syntaxe : SI condition ALORS

Traitements

. FinSI

Exemple
Un algorithme qui calcule le maximum de deux nombres réels.

Algorithme Maximum
Variable A, B, Max : réel ;
Début
        Ecrire ('Entrez les valeurs de A et de B: ') ;
.       Lire (A , B) ;
        Max ←A ;
.      Si Max < B Alors
.              Max← B ;
.       Fin si
.        Ecrire (' Le maximum est égale à :', Max) ;
Fin.

Structure conditionnelle complète (deux choix)

Syntaxe :

SI condition ALORS

// Traitements1

SINON

// Traitemants2

FinSi

Organigramme

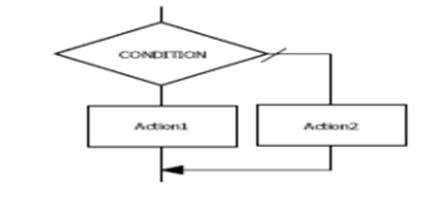
Exemple
Un algorithme qui demande un nombre entier à l’utilisateur, et l’informe ensuite si ce nombre
est positif ou négatif

Algorithme Nature_nombre ;
Variable n : Entier ;
Début
        Ecrire ('Entrez un nombre : ') ;
.       Lire( n) ;
.       Si n > 0 Alors
.              Ecrire ('Ce nombre est positif' ) ;
.          Sinon
.              Ecrire ('Ce nombre est négatif' ) ;
.        Fin si
Fin.

Structure alternative imbriquée

Syntaxe :

Si condition1 Alors

//Traitements1

Sinon

Si condition 2 Alors

// Traitements2 ;

Sinon

// Traitements3 ;

Fin si

Exemple : Etat de l’eau selon sa température (glaçon, liquide, vapeur)

SI la température de l’eau est inférieure à 0° ALORS

- C’est la glace

SINON SI

La température de l’eau est supérieure à 0 et inférieure à 100° ALORS

§ C’est du liquide

SINON

-C’est la vapeur

FinSi

Code :

Algorithme etatEau

Variables A, B : booléens ;

Temp : réel ;

Début

Lire(Temp) ;

A←Temp<=0 ;

B←0<Temp<100 ;

SI A ALORS

Ecrire (‘’C’est la glace ‘’) ;

SINON SI B ALORS

Ecrire (’’ C’est le liquide’’) ;

SINON

Ecrire (‘’ C’est la vapeur’’) ;

FinSi

Fin

LES STRUCTURES ITERATIVES

On utilise les schémas itératifs lorsqu’on veut exécuter une liste d’actions plusieurs fois. Le nombre d’itérations peut être connu ou non. Dans certains cas, on utilise certaines conditions pour contrôler le déroulement des itérations ; on distingue entre autres :

· La structure itérative complète ou la structure POUR … FAIRE …

· Les structures répétitives à condition d’arrêt, composées de deux structures :

_ la structure REPETER … JUSQU’A …

_ la structure TANT QUE … FAIRE …

Ainsi quand on a à écrire une répétitive, on doit d’abord poser la question suivante : est- ce qu’on connait le nombre d’itérations à faire dans la boucle ? Après analyse si la réponse est affirmative on utilise ‘’ POUR ‘’ sinon on utilise ‘’TANT QUE’’ ou REPETER

Instruction d’incrémentation/décrémentation.

L’incrémentation (tout comme la décrémentation) est beaucoup rencontrée dans les structures à boucle. C'est-à-dire dans les structures répétitives. En effet, on peut les assimiler à des compteurs qui, à chaque cycle augmentent ou diminue de 1.Les variables les plus impliquées à cette opération sont les variables de contrôle. On les représente par :

i ← i+1 incrémentation veut dire ’’Ajouter 1 à la valeur actuelle de i’’.

j← j-1 décrémentation veut dire ‘’Retrancher 1 à la valeur actuelle de j’’.

Attention : Il faut généralement initialiser i et j appelés souvent compteurs. Exemple i=0

La structure itérative complète (POUR...FAIRE)

Une structure itérative est dite complète si le nombre de répétition est connu d’avance. Cette structure est caractérisée par :

-l’initialisation automatique du compteur à une valeur initiale V_i

-l’incrémentation/décrémentation du compteur à chaque répétition

-vérification du compteur pour qu’il ne dépasse pas la valeur finale V_f

Syntaxe :

POUR Cp de Vi à Vf PAS de 1 FAIRE

Instruction 1

Instruction 2

….

Instruction n

FinPOUR

Cp : compteur ;

V_i : Valeur initiale=0 ;

V_f: Valeur finale=N

Incrémentation :i←i+1

PAS ou valeur de l’incrémentation : 1

Organigramme :

Exemple : Calculer la somme des 9 premiers chiffres

Algorithme SommeEntiers

Variable Somme : entiers ;

Début

Somme ← 0 ; /* initialisation*/

POUR i=1 à 9 FAIRE

Somme ← Somme +i ;

i ← i + 1

FinPour

ECRIRE (‘’ La somme est :’’, Somme) ;

Fin

Les structures itératives à condition d’arrêt

Une structure itérative est dite à condition d’arrêt si le nombre d’itérations n’est pas connu d’avance, mais il dépend d’une condition.

La structure ‘’TANT QUE …FAIRE ‘’

Avec la structure « TANT QUE », le nombre d’itérations n’est pas à priori connu : Soit c la condition qui prend la valeur « VRAIE » ou « FAUSSE », chaque itération commence par l’évaluation de la condition. Une condition est une comparaison. Elle est composée de 3 éléments : une valeur, un opérateur de comparaison et une autre valeur :

-si la valeur de la condition est vraie, alors on exécute la liste d’action. Les itérations se poursuivent jusqu’à ce que la condition c deviennent fausse :

-si la valeur de la condition est fausse, on n’exécute pas les actions de tant que

Syntaxe :

TANT QUE condition(s) FAIRE

// Traitements

Fin TANT QUE

Organigramme :

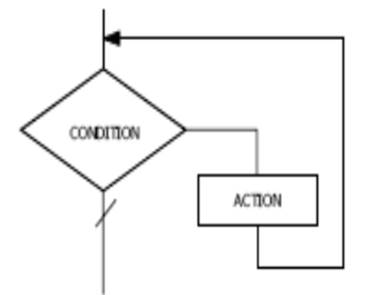
Exemple :

Algorithme Application

Var i,n :entiers ;

Début

i←1 ;

Tant que i<=10 faire

Ecrire (« l’itération est exécutée ») ;

i←i+1

FinTant que

Fin

La structure « REPETER…JUSQU'A »

La structure REPETER…JUSQU'A… est utilisée quand il s’agit de répéter un traitement un nombre de fois inconnu à l’avance et qu’on est sûr que le traitement itératif s’exécutera au moins une fois. Dès que la condition d’arrêt devient vraie, la boucle est abandonnée et le programme continue en séquence.

La structure « REPETER » commence par l’exécution de la liste d’actions. On évalue ensuite la condition :

- si la valeur est fausse, alors, on continue le processus d’itérations

-si par contre, après évaluation de la condition, on trouve qu’elle a pour valeur VRAIE, on sort de la boucle.

Syntaxe :

REPETER

Instruction 1

Instruction 2

….

Instruction n

JUSQU'A condition(s) d’arrêt

Organigramme :

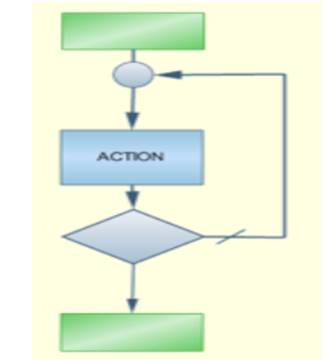
Exemple : Ecrire un algorithme qui dit plusieurs fois « bonjour Monsieur ».

Algorithme bonjour

Var i :entier ;

Début

i←1 ;

Répéter

Ecrire (« bonjour Monsieur») ;

i←i+1 ;

Jusqu’à i>10

Fin

Propriétés

1- Quelle que soit la valeur initiale des conditions, la liste d’action est exécutée au moins une fois

2- Il doit avoir au moins une action qui met à jour la valeur de la condition.

EXERCICES

EXERCICES I:

Exécuter manuellement l’algorithme suivant et déduisez les valeurs finales des variables a, b et c pour chacune des valeurs initiales suivantes de a.

i) a=10

ii) a=3

iii) a=0

Algorithme_Application

Début

Ecrire (« a= ») ;

Lire(a) ;

b←2a ;

c←b-4 ;

Si a>2c alors

b←a-2c ;

sinon

b← a+c ;

FinSi

Ecrire (a, b, c) ;

Fin

EXERCICE II: Soit l’algorithme Suivant :

Algorithme SimpleOuDouble

Const C=10 ;

Var V : entier ;

Début

Ecrire ("Donnez-moi un entier : ") ;

Lire (V) ;

SI V< C ALORS

V ←V*2 ;

Ecrire ("Voici son double :’’, V) ;

SINON

Ecrire ("Voici la valeur inchangée :’’, V) ;

FinSI

Fin

Question : Quels seront les contenus de la variable V après exécution de cet algorithme si au départ, on avait saisi les valeurs 5, 20 et 9 pour V ?

EXERCICE III:

Soit l’algorithme suivant :

1.Algorithme Calcul

2. Variable : X, A, B, i : entiers

3. Début :

4. Ecrire (« Entrer X et A ») ;

5. Lire (X, A) ;

6. B ←1 ;

7. Pour i allant de 1 à X pas =1 Faire

8 B←B*A ;

9. FinPour

10. Ecrire (« résultat= », B) ;

12. Fin

En vous servant de vos connaissances en algorithmique, répondre aux questions suivantes :

1. Définir : variable, constante.

2.a- Identifier dans cet algorithme deux variables.

b-Que fait la ligne 6 ?

3. Identifier la structure de contrôle utilisée dans cet algorithme.

4. Donner la trace d’exécution de cet algorithme pour X=4 et A=3 ;

EXERCICE IV: Soit l’algorithme suivant:

Algorithme

var somme, note : Réels ;

var reponse : Caractère ;

Début

somme ← 0 ;

Ecrire(« Voulez-vous saisir une note o/n ? ») ;

Lire(reponse) ;

Tant que (reponse= « o ») faire

Ecrire(« saisir une note ») ;

Lire(note) ;

Somme ←somme*+ note ;

Ecrire (« Voulez-vous saisir une note o/n ? ») ;

Lire(reponse) ;

Fin Tant que

Ecrire (« La somme des notes est : » , somme) ;

Fin

Questions :

1. Citer les différents types de variables qui sont déclarés.

2. Si un utilisateur saisit les notes : 3, puis 4, puis 12. Quel sera le contenu de la variable somme à la fin du traitement ?

a) 12 b) 7 c) 19 d) 17

3. Que fait cet algorithme ?

4. Est-ce que l’utilisateur peut ne saisir aucune note ? Justifier votre réponse.

5. Dans le contexte de la programmation que fait l’instruction de lecture ?

EXERCICE V :

1-Ecrire un algorithme qui affiche la parité d’un nombre qu’on lui fournit.

2-Concevez un algorithme qui permet de calculer le PGCD de deux nombres non nuls A et B.

3-Ecrire un algorithme qui fait la moyenne de 100 notes des élèves d’une promotion.

EXERCICE VI :

1-Concevez un algorithme qui affiche « Reçu avec mention » si une note est supérieure ou égale à 12, « Passable » si elle est supérieure à 12 et inférieure à 12 et « insuffisant » dans tous les autres cas.

2- Concevez un algorithme qui permet de résoudre l’équation ax +b=0 ; a et b étant les coefficients entiers naturels non nuls de cette équation.

EXERCICE VII :

Soit le circuit électrique suivant :

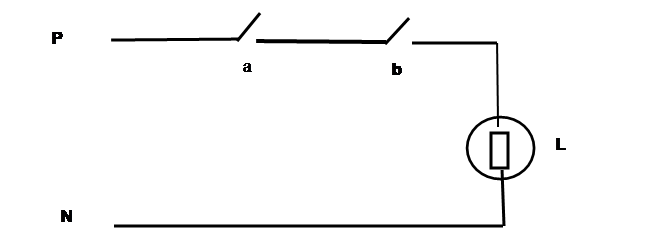
Ce circuit est constitué de deux interrupteurs a et b et d’une lampe L. La lampe L ne s’allume que lorsque les interrupteurs a et b sont fermés à la fois.

On rappelle que :

-Lorsque les interrupteurs a ou b sont fermés, ils prennent la valeur 1 (ou F).

-Lorsque les interrupteurs a ou b sont ouverts, ils prennent la valeur 0 (ou O).

-Lorsque la lampe L est allumée, elle prend la valeur 1 (ou A).

-Lorsque la lampe L est éteinte, elle prend la valeur 0 (ou E).

1-Donner la table de vérité de ce circuit.

2-Proposer un algorithme qui donne l’état de la lampe L en fonction des positions des interrupteurs a et b.

EXERCICE VIII:

Soit l’algorithme suivant :
1.Algorithme Boucle1
2.         Variable i , y : Entiers ;
3.Début
4.         i ← 2 ;
5.         y ← 0 ;

6.         Tant Que (i<7) faire
7.                    i ← i+1 ;
8.                    y ← y+i ;
9.                    Écrire (' Y = ' , y) ;
10.      Fin Tantque
11.      Écrire (‘I=‘, i, ’Y=‘,y) ;
12.
13.Fin

En vous servant de vos connaissances en algorithmique, répondez aux questions suivantes :

a. Identifiez dans cet algorithme une structure de contrôle.

b. Donnez le nombre d’instructions que comporte cet algorithme et énumérez-les.

c. Donnez la trace d’exécution de cet algorithme

d. Proposez un organigramme pour cet algorithme.

CORRIGES

EXERCICE I :

i. a=10 b=26 c=16

ii. a=3 b=5 c=2

iii. a=0 b=8 c= - 4

EXECICE II :

-Pour la valeur 5 ; V=10 ;

-pour la valeur 20 : V=20

-pour la valeur 9 :V=18

EXERCICE III:

1. Variable : objet dont le contenu peut changer par une action lors de l’exécution d’un algorithme

Constante : objet dont le contenu ne changer pas au cours de l’exécution d’un algorithme

2. a-Deux variables : A, B, X, i.

b-Initialise la variable B a 1

3.La structure de contrôle utilisée dans cet algorithme :

Pour i allant de 1 à X pas =1 Faire

B←B*A ;

FinPour

C’est une structure itérative complète.

4. Trace d’exécution de cet algorithme pour X=4 et A=3 ;

Ligne	i	Instructions	B	écran
7	1	B←BA =13=;	3
8	2	B=3*3=	9
8	3	B=9*3=	27
8	4	B=27*3=	81
10				B=81

EXERCICE IV :

1. Réel et caractère

2. c)19

3. Calcule la somme des notes

4. Oui. Il suffit d’attribuer la valeur « n » à réponse et le programme s’arrête.

5. L’instruction de lecture demande à la machine de lire une valeur saisie par un utilisateur à partir du clavier ou de lire une valeur contenue dans une mémoire de stockage. Elle se réduit au verbe LIRE. Lire est donc un ordre de traitement ou une action simple à exécuter.

EXERCICE V :

1-Algorithme NatureNombre ;

Var x, r : entiers ;

Var Nature : chaine ;

Début

Ecrire (‘’ x= ‘’) ;

Lire(x) ;

r ← x mod 2 ;

Si r==0 alors

Nature← ‘’ Paire ‘’;

Sinon

Nature←’’ Impaire’’ ;

FinSi

Ecrire (x,’’ est ‘’, Nature) ;

Fin

2.Algorithme CalculPgcd

Variable A, B : entiers ;

Début

Ecrire ("A = "), Lire(A) ;

Ecrire ("B = "), Lire(B) ;

Tant que A*B !=0) Faire

Si A > B alors

A ← A-B ;

Sinon

B ← B-A ;

FinSi

FinTant que

Si A==0 alors

Ecrire (‘’ pgcd= ‘’, B) ;

Sinon

Ecrire (‘’pgcd= ‘’, A) ;

FinSi

Fin

3. Algorithme Moyenne

Var Som, i : entiers ;

Notes : tableau[1…100 ] d’entiers ;

Début

Som←0 ;

Pour i allant de 1 à 100 Faire

Ecrire (‘’Entrer la note numéro : ‘’, i) ;

Lire (Notes[i]) ;

FinPour

Pour i allant de 1 à 100 Faire

Som←Som + Notes[i] ;

FinPour

Ecrire (“La moyenne est de : ”, Som/100) ;

Fin

EXERCICE VI :

1. Algorithme ReçuAvecMention

Var note : réel ;

Début

Ecrire (‘’ Saisir une note : ‘’), Lire (note) ;

Si note >=12 alors

Ecrire (‘’ Reçu avec mention ‘’)

Sinon si note <12 et note >= 10 alors

Ecrire (‘’ Passable ‘’) ;

Sinon

Ecrire (‘’ insuffisant ‘’) ;

FinSi

Fin

2. Algorithme EquationPremierDégré

Var a, b, x : réels ;

Début

Ecrire (‘’ a= ‘’), Lire (a) ;

Ecrire (‘’ b= ‘’), Lire(b) ;

Si (a==0) et (b==0) alors

Ecrire (‘’ solution infinie ‘’) ;

Sinon si (a==0) et (b != 0) alors

Ecrire (‘’pas de solution dans R ‘’) ;

Sinon

x ← -b/a ;

Ecrire (‘’solution unique ‘’, x) ;

Fin

EXERCICE V II :

o : interrupteur ouvert ou lampe éteinte

1 : interrupteur fermé ou Lampe allumée

a	b	L
0	0	0
0	1	0
1	0	0
1	1	1

2. 2.

Algorithme

Var a, b, l :booléens ;

Début

Ecrire (‘’ a= ‘’), Lire (a) ;

Ecrire (‘’ b= ‘’), Lire(b) ;

Si (a==1) et (b==1) alors

Ecrire (‘’ lampe allumée’’) ;

Sinon

Ecrire (‘’ lampe éteinte’’) ;

FinSi

Fin

EXERCICE VIII:

            Tant Que (i<7) faire
                        i ← i+1 ;
                        y ← y+i ;
                        Écrire (' Y = ‘, y) ;
            FinTantque

b. 04 instructions d’affection

03 instructions d’écriture

02 instructions d’incrémentation

c. Trace d’exécution de cet algorithme

Ligne	i	Instructions	écran

	2	I<7 vrai, on entre dans la boucle y=0 I prend la valeur 3
	3	I<7 vrai , on entre dans la boucle y=0+3=3 I prend la valeur 4
	4	I<7 vrai on entre dans la boucle y=3+4=7 I prend la valeur 5
	5	I<7 vrai on entre dans la boucle y=7+5=12 I prend la valeur 6
	6	I<7 vrai on entre dans la boucle y=12+6=18 I prend la valeur 7
	7	I<7 Faux, on sort de la boucle	I=7 Y=18

Avez-vous un exercice à proposer ? Cliquez-ici