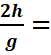CHUTE LIBRE

Un mobile est en chute libre lorsqu’il est soumis à la seule action de son poids. Les autres forces, en particulier la résistance de l’air et la poussée d’Archimède sont négligées. Rigoureusement, les chutes libres ne sont possibles que dans le vide.

Mouvement de chute libre d’un mobile sans vitesse initiale.

Considérons un solide S de masse m lâché en chute libre sans vitesse initiale (v0=0).

 

 

-le système étudié est le solide (S)

 

-le référentiel choisi est le référentiel de laboratoire

-la résistance de l’air étant négligeable, le système n’est soumis qu’à son poids.

 

  Le TCI permet d’écrire :=m

 

m

 

Le vecteur accélération d’un corps en mouvement de chute libre est égal à l’accélération de la pesanteur au lieu de chute. Il ne dépend pas de la masse du solide.

        

Le vecteur accélération est constant, donc le mouvement de chute libre sans vitesse initiale est un mouvement uniformément varié d’équations :

z=gt2

v=-gt

 

Application :

          Un corps tombe en chute libre d’une hauteur h=20m, quelle est sa vitesse à l’arrivée au sol ? On prendra g=10m.s-2.

h=gt2=>t2=

V2=g2t2=g2 2gh    => v===20 m.s-2.

 

 

.       

       z

          O     

 

 

 

                                            

 

 

EXERCICES

EXERCICE I :

            Un corps de masse 5 Kg est lâché sans vitesse initiale à une altitude h =12m du sol.  

1.Déterminer son altitude h2 et sa vitesse à l’instant t2= 1 s.

2.Calculer sa vitesse à l’arrivée au sol.  On prendra g=10m s-2 .

 

EXERCICE II :

            Une bille est lâchée sans vitesse initiale à une altitude h du sol. Elle arrive au sol avec une vitesse v=10m/s.

1. Calculer la hauteur de chute

2. Quelle est la nature du mouvement ?

3. Ecrire l’équation horaire du mouvement. On prendra g=10m s-2 .

 

EXERCICE  III :

 1 : Du haut d’un pont, on laisse tomber un caillou. L’action de l’air est négligeable. Sachant que g= 9,81m s-2 et la hauteur de chute est de 24m, calculer :

11. La durée de la chute.

12. La vitesse du caillou à son arrivée au contact de l’eau.

2 : A la date t = 0 s, on lâche une bille d’un point A situé à une hauteur h du sol ; une seconde plu tard, on lâche une deuxième bille d’un point B situé à 10m en -dessous de A.

Calculer la hauteur h afin que les deux billes arrivent au sol en même temps. On prendra g=10m s-2 .

3 : Un corps de masse m = 20 kg tombant en chute libre arrive sur le sol à la vitesse de 72 km/h. Calculer :

31. La hauteur de chute du corps.

32. La durée de la chute du corps.

 

EXERCICE IV :

             Pour mesurer la profondeur h d’un puits, on laisse tomber du haut du puits une pierre de masse m = 2 kg, sans vitesse initiale. On mesure la durée qui sépare le lâcher de la pierre et la perception du son émis lors de son impact sur l’eau : ∆t = 1,5 s.

Quelle est la profondeur du puits ?

 Données : le son se propage dans l’air à la vitesse : vs = 340 m.s–1 ; On prendra g=10m s-2 .

 

 EXERCICE V ;

          Dans tout le problème, on prendra g= 10m.s-1.

Un mobile homogène (S) de masse m=10-2 Kg est lâché dans l’air sans vitesse initiale à l’instant de date t = 0. La direction du mouvement est la verticale du lieu. La position de (S) est repérée sur un axe vertical orienté vers le bas (Oz). La position de départ de (S) est prise comme origine des espaces (z=0).

Un chronomètre permet la mesure du temps. Au début du mouvement les résultats obtenus sont les suivants :

z(m)

0,03

0,06

0,10

0,15

0,20

t(s)

0,078

0,110

0,141

0,173

0,200

t2(s2)

0,006

0,012

0,020

0,030

0,040

 

1°Tracer la courbe représentative de la fonction z=f(t) (courbe n°1).

2° Déterminer graphiquement le module v1 du vecteur vitesse de (S) à la date t1=0,10s.

3° a)tracer la courbe représentative de la fonction z=f(t2)(courbe n°2).

b)En déduire la nature du mouvement de (S). Calculer son accélération.

c)S’agit-il d’un mouvement de chute libre ? pourquoi ? Sur la figure est représentée la courbe de variations du module v du vecteur vitesse de (S) en fonction du temps.

4° a) Quelle est l’allure de la partie OA de la courbe ? Déterminer l’équation v(t) pour les dates t comprises entre t=0 et t=0,20s.

a)    Quel serait le module du vecteur vitesse de (S) à la date t3=1s si on utilisait l’équation précédemment trouvée pour la vitesse ?

5° a) Déterminer à partir de la figure de la figure le module v3 du vecteur vitesse à la date t3=1s.

    b) Comparer cette valeur à celle trouvée au paragraphe 4° b). Donner une interprétation possible de cette différence.

6° On admet que les différents frottements qui agissent sur (S) sont équivalents à une force unique  qui s’oppose au mouvement de (S). Dans le domaine de vitesse considéré dans le problème (voir figure), le module de  a pour expression R=kv2, k= 10-3 unité SI.

a)   De l’étude dynamique du mouvement de (S) montrer que la direction de  est verticale. En déduire l’expression littérale du vecteur accélération du centre d’inertie de (S).

b)   On admet que la force  peut-être négligée devant le poids  à condition que le rapport soit inferieure ou égal à 4.10-2 . Calculer la valeur maximale de R pour que l’on puisse faire cette approximation. Quelle est la valeur correspondante de la vitesse ?

En déduire l’intervalle de temps correspondant à cette approximation. Calculer alors le module a du vecteur accélération de (S).

c)    Par un raisonnement simple, préciser comment varie a lorsque l’approximation précédente n’est plus valable. En déduire que le module de l’accélération et le module de la vitesse v tendent chacun vers une limite appelée respectivement a1 et v1. Calculer a1 et v1. Quelle est alors la nature du mouvement de(S) ?

d)    Depuis la date t=0, préciser comment varie le module de l’accélération de (S) sur la partie étudiée de la chute. Donner ces valeurs extrêmes.

 

RESOLUTIONS :

EXERCICE I :

Un corps de masse 5 Kg est lâché sans vitesse initiale à une altitude h =12m du sol. 

1. Altitude h2 et sa vitesse à l’instant t2= 1 s.

h2=gt2=5(1)2=2,5m.

v=gt=10(1)=10m.s-1.

2. Vitesse à l’arrivée au sol.

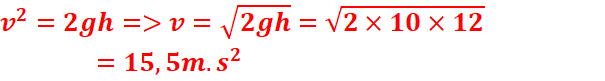
EXERCICE  II :

Une bille est lâchée sans vitesse initiale à une altitude h du sol. Elle arrive au sol avec une vitesse v=10m/s.

1. Hauteur de chute

.

 

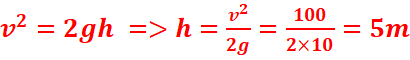2. Nature du mouvement 

a=g=cte    => mouvement rectiligne uniformément varie.

3. Equation horaire du mouvement.

h=g=5t2.

 

EXERCICE  III :

 1 : Du haut d’un pont, on laisse tomber un caillou. L’action de l’air est négligeable. Sachant que g= 9,81m s-2 et la hauteur de chute est de 24m, calculer :

11. Durée de la chute.

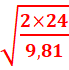h=g=>t====2,33s.

 12. Vitesse du caillou à son arrivée au contact de l’eau.

v=gt=9,81x2,33=22,86m.s-2.

2 : A la date t = 0 s, on lâche une bille d’un point A situé à une hauteur h du sol ; une seconde plu tard, on lâche une deuxième bille d’un point B situé à 10m en -dessous de A. Calculer la hauteur h afin que les deux billes arrivent au sol en même temps. On prendra g=10m s-2 .

3 : Un corps de masse m = 20 kg tombant en chute libre arrive sur le sol à la vitesse de 72 km/h. Calculer :

31. Hauteur de chute du corps.

v=72km/h =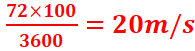

 

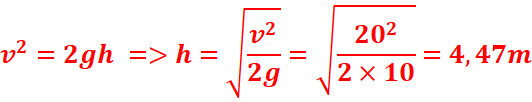
32. Durée de la chute du corps.

v=gt =>t==

 

EXERCICE IV :

  Il faut du temps à la pierre pour atteindre le fond, et il faut du temps au son de l’impact pour remonter jusqu’à l’expérimentateur.

Soit ∆t1, la durée nécessaire pour que la pierre atteigne le fond du puits.

Soit h, la profondeur du puits :  h= g(∆t1)2  soit ∆t1=

  Soit ∆t2, la durée nécessaire pour que le son remonte :  ∆ t 2 = .

La durée totale de l’expérience est : ∆t = ∆t1 + ∆t2, soit ∆t =.

 On pose X = , avec X positif, ce qui donne dans la relation : X2+(vs )X -∆t =0

On résout cette équation du second degré : ∆=+4∆t

 L’équation a deux solutions : l’une positive X1 et l’autre négative X2. C’est la solution positive qui permet de trouver h :10,8m

 

 

Avez-vous un exercice à proposer ? Cliquez-ici

Merci de votre visite
Laissez un commentaire