RESISTANCE
ELECTRIQUE
LOI
D’OHM
Définition.
On
appelle résistor ou conducteur ohmique, une portion du circuit capable
de modifier la valeur de l’intensité du courant électrique.
Son symbole est :
![]()
On mesure la
résistance d’un résistor à l’aide d’un appareil appelé l’ohmmètre.
L’unité de la
résistance d’un résistor est l’ohm de symbole
(Ω).
La loi d’ohm pour un résistor.
Énoncé
de la loi : « La
tension U aux bornes d’un résistor de résistance R est proportionnelle à
l’intensité I du courant qui le traverse ».
On a :
U = R.I avec U(V), I(A) et R(Ω)
Exercice
d’application :
Déterminer la résistance d’un résistor parcouru par un courant d’intensité 2,5A
sachant que la tension à ses bornes est U=3V.
RESISTANCE
ET RESISTIVITE
La
résistance d’un fil homogène de section constante est proportionnelle à sa
longueur l et inversement proportionnelle a sa
section s :
![]()
Le facteur ρ
caractérise la substance du fil, on ‘appelle résistivité. Avec l exprime en mètre
et s en mètres carre, R en ohms, ρ s’exprime en ohm-mètre (Ω.m).
Association des résistances
Résistances
en série

Req
= R1+R2
Résistances
en parallèle

![]()
Conductance :
Le
rapport ![]() est
appelé conductance
est
appelé conductance
La conductance
d’un ensemble de résistance mortes associées en parallèle est égale à la somme
des conductances de chacune d’elles.
On a :
G=G1+G2+G3
Remarques :
1.
La
conductance G est supérieure a chacune des
conductances G1, G2
et G3 dont elle représente la somme.
2.
Par
contre, la résistance équivalente est plus petite que la plus petite des
résistances associées en parallèle.
3.
Dans
le cas particulier de l’association de n résistances mortes de même valeur R1.
4.
G=nG1 ou R=R1/n
Shunt
des ampèremètres
Shunter
un ampèremètre, c’est placer en dérivation entre ses bornes un résistor s,
appelée shunt de façon que l’appareil ne soit traverse que par une fraction
connue du courant à mesurer.

Si r désigne la
résistance de l’ampèremètre, l’intensité du courant à mesurer est l’intensité
lue sur la graduation multipliée par le nombre
![]() est appelé multiplicateur de shunt.
est appelé multiplicateur de shunt.
CARACTERISTIQUE
INTENSITE-TENSION : Détermination expérimentale de la résistance d’un
résistor
Soit
le circuit ci-dessous constitué d’un générateur, d’un rhéostat, d’un
ampèremètre, d’un résistor et d’un voltmètre.

En déplaçant le
curseur du rhéostat, l’intensité du courant varie dans le circuit ainsi que la
tension aux bornes du résistor. On obtient expérimentalement les
résultats :
|
I(mA) |
0 |
15 |
30 |
45 |
60 |
|
U(V) |
0 |
1 |
2 |
3 |
4 |
Représentation
graphique
Représentons
alors la caractéristique intensité tension de ce résistor : 1cm pour 1V et
1cm pour 15mA.

La courbe
obtenue est appelée caractéristique intensité –tension du résistor.
C’est une droite
linéaire passant par l’origine du repère.
EXERCICES
EXERCICE
I :
1.Quelle est la
résistivité de l’alliage constituant un fil de longueur l=4 m et le diamètre
D=0,2 mm dont la résistance est R=60 Ω ?
2.Calculer la
longueur d’un fil homogène de section constante s=1mm2 dont la
résistance est 1 Ω. La résistivité du fil est 8.10-7 Ω.m.
3.Calculer la
résistance d’un fil d’argent de 0,8 mm de diamètre recouvert d’une couche
d’isolant de 0,1mm d’épaisseur, bobiné à spires jointives sur un cylindre
isolant de 1 m de long et de 3 cm de diamètre.
Résistivité de
l’argent : ρ=1,6.10-8 Ω.m
EXERCICE
II :

La tension aux bornes aux bornes du générateur vaut 12V et la tension aux
bornes de la résistance vaut 8,5V. La résistance de R vaut 17 Ω et la
résistance R1 de la lampe vaut 7Ω.
1.
Indiquer le sens du courant.
2.
Combien vaut la tension aux bornes de la
lampe ?
3.
Calculer l’intensité I du courant qui traverse le
circuit.
EXERCICE
III :
Un
courant de 5 A se partage entre deux résistors de 2 ohms et 3 ohms associées en
parallèle.
1.Calculer les
intensités des courants dérivés.
2.La résistance
équivalente à l’association
3.La ddp entre les extrémités de celle-ci.
EXERCICE
IV :
Un
ampère est shunté au 1/10 (l’ampèremètre est traversé par le dixième du courant
à mesurer). Sa résistance propre est 0,1 Ω.
1.Quelle est la
résistance du shunt.
2.Sachant que
ce shunt est un fil de 0,8 mm de diamètre et de résistivité ρ=1,6.10-8
Ω.m. calculer sa longueur.
EXERCICE V :
Dans l’association de conducteurs ohmiques de la
figure ci-dessous, les conducteurs ohmiques utilisés ont pour résistances : R1
= R2 = 20 Ω et R3 = 80Ω. On applique entre A et C la tension UAC
= 24 V.
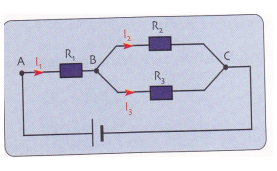
1. Déterminer la valeur de la résistance Re équivalente au dipôle AC.
2. En déduire la valeur de I1.
3. Calculer les tensions UAB et UBC.
4. En appliquant la loi d’Ohm, déterminer I2 et I3.
La loi des nœuds est-elle vérifiée sachant que l’on tolère un écart relatif
inférieur à 4,0%
CORRIGES
EXERCICE I :
1.
R=ρl/s
=>ρ=Rs/l
s=πr2=πD2/4=3,14x(0,2.10-3)2/4=0,0314.10-6m2.
ρ=Rs/l=60x0,0314.10-6/4=0.471.10-6 Ωm
2.
R=ρl/s
=>l=Rs/ρ=1x10-6/8.10-8=0.125x100=12,5m
3.
Nombre
d’enroulements du fil : N=L/d+e
=1/(0.8+0,2)10-3=1000 spires
Longueur
du fil : l=πDN=3,14x3.10-2x1000=94,2 m
Section
du fil ; s=πd2/4=3,14(0,8.10-3)2/4=0,5.10-6
m2.
R=ρl/s =1,6.10-8x94,2/0,5.10-6=3
Ω
EXERCICE II:
1.Le courant sort par le + et rentre par le – donc
sens P→C→D→N.
2.VPN=VP-VC +VC-VE+VE-VD+VD-VN
12 =0
+ VC-VE +8.5
+0 =>VC-VE=12-8,5=3,5
V
3. UR=RI => I=UR/R=8,5/17=0,5 A.
I=12/(17+7)=12/24=0,5A
I=3,5/7=0,5 A
EXERCICE III :
1.Soit
U la tension fournie par le générateur, R1=2Ω et R2=3Ω
U=R1I1=R2I2
avec I=I1+I2
I=I1+I2 => I1=I-I2
R1(I-I2) = R2I2 <=> 2(5-I2)=3I2 =>I2=2 A
I1=I-I2=5-2=3
A
2.La résistance
équivalente à l’association
![]()
3.U=ReqI=6/5x5=6 V
EXERCICE IV :
1.
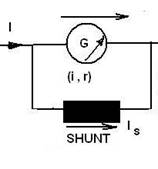
On a: I=i +Is et ri=sIs
·
I=i +Is
ð I=nI +Is=0.1I +Is <=>I(1-0,1)=Is => Is=0,9I
·
ri=sIs
<=>r(I-Is)=sIs <=>0,1(0,1I)=sx0,9I =>s=0,1(0,1I)/
0,9I=0,01/0,9=0,0111Ω
2. R=ρl/s
=>l=Rs/ρ
s=πr2=πD2/4=3,14x(0,8.10-3)2/4=0,5.10-6
m2
l=Rs/ρ
=0,0111x0,5.10-6/1,6.10-8=35 cm
EXERCICE V :
1. (R2 et R3 en dérivation alors R2,3 = (R2.R3) /
(R2+ R3 )
on trouve R2,3 =16 Ω
Re(AC) = R1 + R2,3 car en série on trouve Re = 36Ω
2.
Schéma équivalent puis UAC = Re .I1 (Loi
d’Ohm) alors 24 = 36 I1 et I1 = 0,67 A (c’est 2/3 A)
3. UAB = R1.I1 = 20
. 2/3 ≈13 V
* Additivité
des tensions : UAC = UAB + UBC on trouve UBC
= 11 V
4.
* La loi
d’Ohm pour R2 : UBC = R2.I2 alors I2
= 11/20 = 0,55 A
* De même
pour R3 : UBC = R3.I3 et I3
= 11/80 = 0,14 A
*La loi des nœuds : I1 = I2 +
I3 on a d’une part I1 = 0,67 A et I2 + I3
= 0,55 + 0,14 = 0,69A L’écart relatif est : (0,69 – 0,67) / 0,67 ≈ 3,0 %
< 4,0% loi des nœuds vérifiée.
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire