PROPRIÉTÉS DE PYTHAGORE ET TRIGONOMÉTRIE

PROPRIÉTÉS DE PYTHAGORE

Définitions

Soit un triangle ABC rectangle en A

Théorème :

Dans un triangle rectangle la somme des carrés des cotés adjacents et côtés opposés est égale au carré de l’hypoténuse.

AC²+AB²=BC²

TRIGONOMÉTRIE

Sinus d’un angle

Dans un triangle ABC rectangle en A , on définit le sinus, de l’angle aigu de la manière suivante :

Propriétés
Ø Le sinus d’un angle aigu est strictement plus grand que 0 et strictement plus petit que 1
Ø Lorsqu’on connait le sinus, d’un angle, on peut trouver la mesure de cet angle en
utilisant respectivement les touches shift et sin pour activer la touche sin^-1 de la calculatrice scientifique.

Exemple : Trouvons l‘angle dont le sinus vaut 0,8.

La touche shift combinée avec sin^-1(0,8) donne 53,13

Cosinus d’un angle

Dans un triangle ABC rectangle en A , on définit le cosinus de l’angle aigu de la manière suivante :

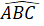
Propriétés :
Ø Le cosinus d’un angle aigu est strictement plus grand que 0 et strictement plus petit que 1
Ø Lorsqu’on connait le cosinus, d’un angle, on peut trouver la mesure de cet angle en
utilisant respectivement les touches shift et cos pour activer la touche cos^-1 de la calculatrice scientifique.

Exemple : Trouvons l‘angle dont le cosinus vaut 0,8.

La touche shift combinée avec cos^-1(0,8) donne 36,87.

Tangente d’un angle

Dans un triangle ABC rectangle en A, on définit la tangente de l’angle aigu de la manière suivante :

Exemple : Calculons la tangente de l’angle

Propriétés fondamentales

Si ɑ est un angle aigu :

sinɑ =.

cosɑ =

tanɑ =

sin²ɑ +cos²ɑ = 1

or sinɑ = et cosɑ = => ()² + ()²= 1 => AC²+AB²=BC² (Théorème de PYTHAGORE)

Cosinus et sinus des angles remarquables

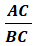
Remarque : le sinus, le cosinus et la tangente d’un angle n’ont pas d’unité.

EXERCICES

EXERCICE I :

1. ABC est un triangle rectangle en A tel que : AB = 16 cm AC = 12 cm Calculer la longueur BC.

2. ABC est un triangle rectangle en C tel que : AB = 16 cm AC = 12 cm Calculer un arrondi au mm de la longueur BC.

3. IJK est un triangle tel que : IJ = 3,6 cm IK = 6 cm JK = 4,8 cm Démontrer que IJK est un triangle rectangle.

4. a-Construire un triangle IJK tel que ; IJ=6cm ;JK=8 cm et IK=10 cm.

b-Quel cote représente l’hypoténuse ?

c-Montrer que IJK est rectangle.

EXERCICE II :

On considère le triangle EFG ci-dessous, rectangle en F tel que : FG=4Ѵ3 ; EG=8 et mesure

L’unité est le mètre.

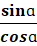
1. Calcule EF

2. Calcule le rapport .

3. A l’aide de ta calculatrice scientifique, utilise la touche sin pour calculer sinus de 60° noté : sin60 et compare avec la question 2).

4. Vérifier le calcul de 1) par la formule :

EXERCICE III:

Soit α la mesure d’un angle aigu tel que sinα=0,4.

1.Calculer la valeur de cosα

2.En déduire la valeur de tanα.

3.Verifier la formule :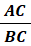

EXERCICE IV :

Un client a choisi un écran dont voici les dimensions :

1) Calculer la diagonale AC de l’écran. Arrondir à 0,1 cm.

2) Un écran est dit « 16/9ème » lorsque ses dimensions 16 vérifient la relation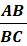

L’écran précédant est-il un « 16/9ème » ? Justifier la réponse.

EXERCICE V :

Situation

Quatre concessions R, O, D et E doivent être éclairées par un lampadaire placé en U.C₁ et C₂ sont des cercles circonscrits respectivement aux triangles ROU et UGE. Le rayon d’action du lampadaire L est de 20 m . Les droites (RO) et (GE) sont parallèles.

On donne :RU=20m ; UE=30m et UO=16m.

Taches :

1 : Quelle est la nature des triangles ROU et UGE ?

2 : La concession G est-elle éclairée ? justifier votre réponse par des calculs.

3 : Quelle est la distance qui sépare les concessions E et F

EXERCICES VI :

Situation :

Abena est propriétaire d'un champ, représenté par le triangle ABC ci-dessous. Il achète à son voisin le champ adjacent, représenté par le triangle ADC. On obtient ainsi un nouveau champ formé par le quadrilatère ABCD. Dans la partie ADC, Abena voudrait cultiver les arachides et les vendre pour financer l’exploitation de la partie ABC qui nécessite 500000 FCFA. La rentabilité du champ d’arachide est estimée à 1250F/m². Abena sait que le périmètre de son champ ABC est de 154 mètres et que BC = 56 m. Son voisin l'informe que le périmètre du champ ADC est de 144 mètres et que AC = 65 m. De plus, les longueurs AB et DC sont respectivement égales à 33 m et 63 m. La municipalité exige une taxe foncière de 126frs/m²

Taches :

1. Abena pourra-t-il financer l’exploitation du champ ABC ?

A_(ADC)= DCxAD/2

AC²=AD²+DC² =>AD²=AC²-DC²=65²-63²=4225-3969 =256=>AD=16 m

A_(ADC)=63x16/2=504m²

Montant des arachides :504x1250=630 000 FCFA

Abena pourra financer la partie ABC

2. Combien devra-t-il payer à la commune pour tout son champ.

Aire du champ ABCD=A_(ABC) + A_(ADC).=AB.BC/2+DC.AD/2= AB.BC/2+504=33x56/2+504=924+264=1428m².

1428x126= 1 799 28frs

3. Abena veut clôturer son champ avec du grillage. Le grillage coute 600 frs le mètre : Combien va-t-il payer pour clôturer son champ ?

Le périmètre est 164+144=308m

Prix à payer :308x600= 184 800 FCFA

CORRIGES

EXERCICE I :

1. D’après le théorème de Pythagore dans le triangle BAC rectangle en A, on a : CB² = CA² + AB² CB² = 12² + 16² CB² = 144 + 256 CB² = 400 CB = 400 = 20 cm

2 . D’après le théorème de Pythagore dans le triangle BCA rectangle en C, on a : AB² = CA² + CB² 16² = 12² + CB² 256 = 144 + CB² CB² = 256 – 144 CB² = 112 CB = 112 » 10,6 cm

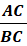
3. IK² = 6² = 36 IJ² + JK² = 3,6² + 4,8² = 12,96 + 23,04 = 36 D’où IK² = IJ² + JK² Donc d’après le théorème de Pythagore, le triangle IJK est rectangle en J.

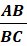
Le cote qui représente l’hypoténuse est le cote IK

IJ2=62=36 ; JK2=82=64 ;IK2=102=100

Comme 64+36=100 alors IJK est rectangle en J

EXERCICE II:

1. D’après le théorème de Pythagore :

EG²=EF²+FG² =>EF²=EG²-FG²=8²-(4Ѵ3)²=64-16.3=64-48=16 =>EF=4 m.

2. Calculons le rapport .

3. Avec la calculatrice scientifique, on trouve : sin60=0,866025403

Comparaison :

4. Vérification :

EXERCICE III:

1. sin²ɑ +cos²ɑ = 1 =>cos²α=1- sin²ɑ=1-(0,4)²=0,84 =>cosα=Ѵ0,84=0,91651.

EXERCICE IV:

1. D’après le théorème de Pythagore :

AC²=AD²+DC²=8,6²+15,3²=73,96+234,09=308,05 =>AC=17,55

2.Oui

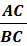
EXERCICE V :

Tache 1 :

Le point O est sur le cercle de diamètre [RU] donc le triangle ROU est rectangle en O. Le point G est sur le cercle de diamètre [UE] donc le triangle UGE est rectangle en G.

Tache 2 :

UO.UE=UG.RU =>UG=

La concession G est éclairée car UG<25m

Tache 3 :

Le triangle UGE est rectangle en G

On a : UE²=UG²+GE² =>GE²=UE²-UG²=30²-24²=324 =>GE=18 m

Avez-vous un exercice à proposer ? Cliquez-ici