GENERALITES SUR LES ALGORITHMES
INTRODUCTION
Définitions
Un algorithme est une
suite d’actions ou d’instructions qui doivent être exécutées dans
un ordre bien déterminé pour résoudre un problème (ou réaliser un
travail) en un temps fini.
L'algorithmique
est l’ensemble des règles et des techniques qui sont impliquées dans la
définition et la conception d'algorithmes.
Si les instructions
d'un algorithme s’exécutent les unes après les autres, l'algorithme est dit séquentiel,
si elles s’exécutent en même temps, il est parallèle. Si l'algorithme
exploite des tâches s’exécutant sur un réseau de processeurs on parle d’algorithme
réparti, ou distribué.
Caractéristiques d’un bon algorithme
Un algorithme doit
avoir les propriétés suivantes :
-clarté : il doit
être facile à comprendre et à interpréter
-documenté : On doit insérer des
commentaires qui étayent la compréhension du programme.
-précis : chaque
élément de l’algorithme ne doit pas prêter à confusion, il est donc important
de lever toute ambiguïté ;
-efficacité :
Les opérations doivent être suffisamment simples et s’exécuter le plus
rapidement possible.
Importance de l’algorithme.
Un algorithme, traduit dans un langage
compréhensible par l’ordinateur (ou langage de programmation), donne un programme
informatique, qui peut ensuite être exécuté pour effectuer le traitement
souhaité. Donc l’algorithme facilite l’écriture des programmes informatiques.
Si un programme informatique était une dissertation, l’algorithme devait
constituer le plan de cette dissertation.
L’écriture algorithmique est un travail de programmation à visée «universelle». En effet, un algorithme ne dépend pas :
-du langage dans lequel il est implanté,
-ni de la machine qui exécutera le programme correspondant.
Etapes de résolution d’un algorithme
Les trois étapes de résolution d’un algorithme sont :
-Préparation du
traitement : Recherche des données nécessaires à la résolution du problème
-Traitement :
résolution pas à pas, après décomposition en sous-problèmes si nécessaire
-Edition des
résultats : impression à l’écran, dans un fichier, etc.
Représentation des algorithmes
On
utilise généralement une série de conventions appelées LDA (Langage de Description
des Algorithme), ou par un algorigramme
(représentation graphique des algorithmes).
TYPES DE
DONNEES UTILISEES EN ALGORITHMIQUE
Les
données sont des informations nécessaires au déroulement d’un algorithme. .
Les constantes
Définition
Une
constante est une donnée fixe qui ne
varie pas durant l’exécution d’un algorithme.
Une
constante est caractérisée par son nom et sa valeur (fixe).
Déclaration
des constantes
Pour déclarer une constante, on
écrit le mot-clé const,
suivi du nom de la constante et de sa valeur.
Syntaxe :
const nom _Constante = valeur ;
Exemples:
const Pi=3,14 ;
const Max=100 ;
const Mois= ‘Avril’ ;
Codification des objets
|
|
Objet |
Type/Nature |
Rôle |
|
Général |
Nom |
Constante=valeur de la constante |
Rôle |
|
Exemple |
Pi |
3,14 |
|
Les variables
Définition
Une variable est un objet dont le contenu peut être modifié par une action
durant l’exécution d’un algorithme.
Une
variable est caractérisée par son nom, sa valeur et son type :
Exemple : age_du_visiteur =17.
Nom : pour pouvoir
reconnaitre la variable (age_du_visiteur).
Valeur
: c'est l'information qu'elle contient, qui peut changer. (17).
Type :
entier
Remarques :
1) Le nom
d’une variable doit commencer obligatoirement par une lettre. Il doit être
formé d’une ou de plusieurs lettres, les chiffres sont également autorisés.
Aucun espace ne doit figurer dans le nom d’une variable. Il vaut mieux
remplacer les espaces par la touche (underscore) « _ » du clavier. De même, il est préférable que
le nom donné à une variable soit évocateur de l’information qu’elle contient.
2) On peut
modifier quand on veut la valeur d’une variable, faire des opérations dessus,
etc.
Les différents types de variables
Les variables sont capables de stocker
différents types d'informations. On parle de types de données. Voici les principaux types à connaître :
Les types
numériques :
Les
types numériques les plus connus sont l’entier et le réel :
·
Le type entier (int)
: ce sont les nombres
du type 1, 2, 3, 4, etc. On compte aussi parmi eux les nombres relatifs : -1,
-2, -3...
Exemple : 42
·
Le type réel :
Le
type réel recouvre un ensemble de nombres réels qui ne correspond pas toujours
aux réels en mathématiques. Il comprend les
nombres décimaux (float)
qui sont des nombres à virgule, comme 14,738. Le
traitement et l’affichage des données de ce type se font à virgule flottante,
c’est à-dire qu’il est possible de les écrire en déplaçant le point à volonté
et en utilisant une puissance
appropriée dans la base choisie.
Exemple : 235.67=
0.23567.103=23467.10-2
On
note aussi 0.23567E3 ou 23467E-2.
Le type booléen (bool) :
C’est un type très important qui ne
permet de stocker que deux valeurs, par exemple vrai ou faux (on écrit true pour vrai,
et false pour faux).
Une
variable type booléen ne peut prendre que deux valeurs représentées par les
identificateurs Vrai ou Faux.
Exemple : 14>5 est
Vrai
14<5 est Faux …. sont des expressions booléennes.
Le type
caractère :
Il
appartient à l’une des catégories suivantes :
- Les chiffres de 0 à 9
- Les lettres de l’alphabet (de A à Z)
majuscules et minuscules.
- Les caractères spéciaux +,-,*, / ; etc.
qui correspondent aux touches du clavier, y compris les touches de fonction
telles que la barre d’espacement et la touche entrée.
Une
variable caractère occupe un octet en mémoire. A chaque caractère correspond un code
(appelé code ASCII) qui est un entier compris entre 0 et 255.
Remarques :
-Un caractère est généralement placé entre
2 guillemets.
Exemple :
‘’ a ‘’ ; ‘’ g’’ ; ‘’ 128 ‘’.
-Un caractère vide est représenté par
deux paires de guillemets ‘’ ‘’
-Une variable de type caractère ne peut
contenir qu’un et un seul caractère
-Tous les caractères sont ordonnés selon
leur code ASCII variant de 0 à 255.
Le type chaine de
caractères
Une chaine
de caractère est un regroupement de plusieurs caractères. La chaîne de
caractères est le nom informatique qu'on donne au texte. On peut stocker des textes courts comme de
très longs textes au besoin.
Exemples:
·
"Je
suis un texte". Une chaîne de caractères est habituellement écrite entre
guillemets ou entre apostrophes (on parle de guillemets simples) : 'Je suis un
texte'. Les deux fonctionnent mais il ne faut pas les mélanger.
·
« bonjour »
Attention : 234 peut désigner le nombre deux cent trente- quatre comme
il peut désigner une suite de caractère 2, 3,4. Dans ce dernier cas, on écrit
entre guillemets ‘’ 234 ‘’ pour faire la différence.
Déclaration d’une variable
Pour déclarer une variable, on écrit
le mot-clé var, suivi du nom de la variable et du type.
Syntaxe :
var nom_de_la_variable :
type ;
Exemples :
var age :
entier ;
var a :
caractère ;
var nom : chaine de
caractères ;
var i,j,k :entiers ;
Tableau
de codification des objets
|
|
Objet |
Type/Nature |
Role |
|
General |
Nom |
Type de la variable |
Rôle
joué par la variable |
|
Exemple |
M |
Reel |
|
INSTRUCTIONS
SIMPLES
Une structure est dite simple
(appelée encore une séquence), si
elle ne contient que des instructions :
- d’entrée de données,
- d’affectation
- de sortie de résultats.
Instruction de lecture (ou opérations d’entrée
des données)
L’instruction de lecture demande à
la machine de lire une valeur saisie par un utilisateur à partir du clavier ou
de lire une valeur contenue dans une mémoire de stockage. Elle se réduit au
verbe LIRE. Lire est donc un ordre
de traitement ou une action simple à exécuter.
Ainsi Lire une
valeur « a » donne un ordre à l’utilisateur d’entrer ou de saisir cette valeur à l’aide du clavier de
l’ordinateur ou à partir d’une mémoire de stockage.
Syntaxe : Lire (variable) ;
Exemples :
Lire (note) ;
Lire (A, B) ; A et B étant des
variables.
Instruction d’écriture (ou opération de sortie
des résultats)
L’instruction d’écriture demande à la
machine d’afficher le résultat d’un traitement à l’écran. Elle se réduit au
verbe ECRIRE. Comme Lire, Ecrire est
une action à exécuter , un ordre de traitement
dont le sens traduit en quelque sorte l’action d’afficher un résultat ou autre chose dans une unité de
sortie de l’ordinateur comme le moniteur, l’imprimante ou un support de
stockage.
Syntaxe : Ecrire(variable) ;
Ecrire (‘’ message’’, variable)
Exemples : Ecrire(Résultat) ;
Ecrire ('’Le résultat est :'’, Résultat) ;
Instruction d’affectation
Cette
instruction permet de ranger une
valeur dans une variable. Elle se symbolise par ←.
Syntaxe : Variable ← valeur
Exemples : x ← 35
veut dire que x prend la valeur 35.
A ←2
: la variable A reçoit la valeur 2
B←A+1 : la variable B reçoit le contenu de A plus 1
Nom←'Mohamed' : la variable Nom
reçoit la valeur Mohamed
LES PARTIES D’UN ALGORITHME
Le profil (en-tête)
La
première ligne d’un algorithme est le profil. Elle donne essentiellement le nom
de l’algorithme. Les débuts de mots sont en lettres majuscules.
Exemple : Algorithme_CalculSurface
Déclaration des variables et des constantes
Après
le profil, suivent les déclarations des variables. Ces variables sont de divers
ordres : les réels, les entiers, les chaines de caractère…
En
général, ces variables sont des valeurs d’entrée de l’algorithme. Après
traitement, ce sont les mêmes variables qui permettent d’obtenir des valeurs de
sortie. Les variables d’entrée et de sortie doivent être précisées entre le
profil et le délimiteur du début de l’algorithme, ensuite les constantes, les
fonctions et les tableaux suivront.
Les délimiteurs de début et de fin.
Comme
leur nom indique, les délimiteurs représentent le début et la fin de l’algorithme.
Le corps de l’algorithme
Le
corps de l’algorithme représente la zone où les différentes actions de
l’algorithme se situent. En général, le patron d’un algorithme ou structure
peut se résumer par les lignes suivantes.
|
Algorithme Nom_
Algorithme.
Variables Entrée
Sortie.
Début Action1
Action2 Action n Fin |
← profil ←
variable d’entrée ←variable de sortie
← différentes actions ← délimiteur de fin |
Les commentaires
Les commentaires sont
souvent utilisés pour permettre une interprétation aisée de l’algorithme. On
les place entre /* et
*/ ou (ou entre co et fco).
1-Ecrire (« Entrer la valeur de l’entier a :») ;
2- Lire
(a) ; /* on saisit la valeur de l’entier a au
clavier */
3-Ecrire
(« Entrer la valeur de l’entier b : ») ;
4-
Lire (b) ; /* on saisit la valeur de l’entier b au clavier
*/
4-S← a+b;
5-Ecrire (« La somme S
est : », S); /* On affiche le résultat à l’écran */
OPERATEURS ET EXPRESSIONS
OPERATEUR
Un opérateur est un signe qui relie deux
valeurs, pour produire un résultat.
Les opérateurs possibles
dépendent du type des valeurs qui sont en jeu.
Opérateurs numériques
Ce sont
les quatre opérations arithmétiques et tout ce qu’il y a de classique.
+ : addition
- : soustraction
* : multiplication
/ : division
^ : qui signifie
« puissance ». 45 au carré s’écrira donc 45 ^ 2.
DIV
(A, B) : donne le quotient de la division entière de A par B
MOD
(A, B) : donne le reste de la division entière de A par B
Exemples : A=5
et B=2
A/B=2.5
DIV(5,2)=2 ;
MOD(5,2)=1.
Operateurs de comparaison
<strictement inférieur
> strictement supérieur
<=
inférieur ou égal >= supérieur ou égal
= égal
<> différent de
Opérateur alphanumérique :
&
Cet
opérateur permet de concaténer,
autrement dit d’agglomérer, deux chaînes de caractères.
Exemples
. Variable : A ;
B ; C en caractères
A← ‘’Michel’’
B← ‘’ Amougou’’
C← A &B
//La valeur de C à la fin de l’algorithme est "MichelAmougou"
Opérateurs logiques
Il s’agit
du ET, du OU, du NON et de XOR.
Opérateurs de type booléen
Ils sont de la
forme :
-VRAI ou FAUX
-OUI ou NON
On obtient un résultat de type
booléen quand on est amené à comparer des expressions entre elles, au moyen des
opérateurs de comparaison.
EXPRESSION
Une expression est un ensemble de valeurs,
reliées par des opérateurs, et équivalent à une seule valeur. Par exemple,
voici quelques expressions de type numérique :
7
5+4
123-45+844
Toto-12+5-Riri
…sont toutes des expressions
valides, pour peu que Toto et Riri soient bien des
nombres car dans le cas contraire, la quatrième expression n’a pas de sens.
|
Expression |
Résultat |
|
20>4 |
Vrai |
|
12<=5 |
Faux |
|
30>5 et 5<3 |
Faux |
Priorité des opérateurs
Pour les
opérateurs arithmétiques donnés ci-dessus, l’ordre de priorité est le suivant
(du plus prioritaire au moins prioritaire).
( ) :
Les parenthèses.
^ : Élévation à la
puissance
*,/ :multiplication,
division.
+,- :
addition, soustraction
En cas de besoin, on utilise les
parenthèses pour indiquer les opérations à effectuer en priorité. A priorité
égale, l’évaluation de l’expression se fait de la gauche vers la droite.
Exemples :
1+ (2*3)=7
1*(2+3)=5 /* les
parenthèses sont prioritaires */
1*2+3=5
1+2*3=7 . /* la multiplication est prioritaire
sur l’addition */
3*3^2=27
3^3*2=54 /* la puissance est
prioritaire sur la multiplication */
1+3-2=2
1-3+2=0 /* à priorité
égale, l’évaluation se fait de la gauche vers la droite*/
On a le
droit d’utiliser les parenthèses, avec les mêmes règles qu’en mathématiques. La
multiplication et la division ont « naturellement » priorité sur
l’addition et la soustraction. Les parenthèses ne sont ainsi utiles que pour
modifier cette priorité naturelle.
Cela signifie qu’en
informatique, 12 * 3 + 5 et (12 * 3) + 5 valent strictement la même chose, à
savoir 41
En revanche, 12 * (3 +
5) vaut 12 * 8 soit 96.
LES ALGORIGRAMMES
1-Définition
C’est la représentation
graphique des algorithmes avec des figures géométriques (rectangles,
parallélogrammes, losanges, etc.). On les appelle souvent logigramme,
organigramme et rarement ordinogramme.
2-Symboles
|
Marque
le début ou la fin d’un algorithme.
Marque les instructions de lecture ou d’écriture
Marque une action simple à exécuter.
Représente un sous-programme
Marque
une question posée par l’évaluation d’une condition C qui a la valeur soit
« vrai », soit « faux ». O Anneau numéroté utilisé pour les algorithmes longs de plus
d’une page. Il permet de repérer la fin de la première page et le début de la
seconde. |
|
![]()
Flèche de connexion pour indiquer le sens de
lecture
Exemple :
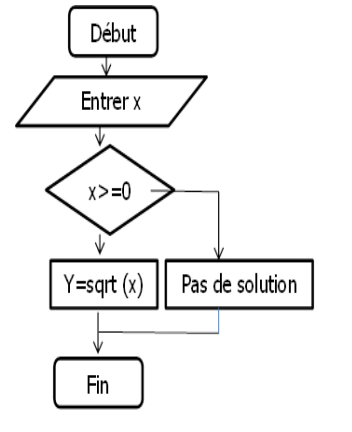
EXERCICES
.
EXERCICE
I : soit l’algorithme
ci-dessous :
Algorithme
Var nb,
pht, ttva ; pttc :
Numérique ;
Début
Ecrire ‘’Entrez le prix hors taxes :’’ ;
Lire (pht) ;
Ecrire (‘’Entrez le
nombre d’article :’’) ;
Lire (nb) ;
Ecrire (‘’Entrez le
taux de TVA :’’) ;
Lire (ttva) ;
pttc⃪nb*pht*(1+ttva) ;
Ecrire (‘’ Le prix
toutes taxes confondues est :’’, pttc) ;
Fin
Questions :
1.1-Que vaut pttc lorsque nb=5, pht=7500 fcfa et ttva=7% ?
1.2-Que fait cet algorithme ?
EXERCICE II :
Votre grand-père détient une
parcelle sous forme rectangulaire au village. Il sollicite votre aide pour
connaitre la superficie de son terrain
- Analyse du
problème
a-Identifier le(s) éléments en entrée
b-Quels sont
les opérations (traitements)
c-Identifier le(s) éléments en sortie
- Faire un tableau
récapitulatif des objets (nom de l’objet, type/nature et le rôle joué par
chaque objet) nécessaire à la réalisation de ces opérations.
- Ecrire un
algorithme qui permet de résoudre ce problème
EXERCICES III :
1-On se propose de
déterminer l’allongement Δl d’un ressort de
raideur K sur lequel est accrochée une masse m.
Sachant que :
Δl *K=m*g avec g=9,8 N/Kg.
2-Faire un tableau
récapitulatif des différents objets (nom de l’objet, type/nature, rôle joué par
l’objet.
3-Faire la déclaration des différents objets.
4-En
déduire l’algorithme qui permet de calculer l’allongement de ce ressort.
EXERCICES IV :
1-Ecrire un
algorithme permettant de calculer la surface d’un cercle de rayon R.
2-Concevez un algorithme qui calcule le carré d’un nombre
qu’on lui fournit.
3-Ecrire un algorithme qui calcule le prix TTC (toutes
taxes comprises) lorsqu’on lui fournit le prix HT (Hors taxes) lorsqu’on
connait le taux de la TVA.
On rappelle que le prix TTC=prix HT + prix HT*TVA/100=prix
HT*(1 + TVA/100).
4-Ecrire un algorithme qui permet de Calculer et afficher le
quotient et le reste de la division de A par B, A et B étant des réels entiers
non nuls
EXERCICE I :
1-pttc =5x7500x (1 + 7/100) =40 125
2-Cet algorithme calcule et affiche le prix
toutes taxes comprises d’un article en fonction de la quantité, du prix hors
taxe et de la tva
3-Calcul_pttc
EXERCICE
II :
1. a-Longueur L, largeur l
b-Multiplier la longueur par la largeur (L * l)
c-Surface (S)
2.
|
Objet |
Type/Nature |
Rôle |
|
L |
Réel |
Longueur de la parcelle |
|
l |
Réel |
Largeur de
la parcelle |
|
S |
Réel |
Surface de
la parcelle |
3.
Algorithme surfaceRectangle
Var L, l : Réel ;
Début
Écrire ("Entrer la longueur du
rectangle :") ; Lire (L) ;
Écrire ("Entrer la largeur du
rectangle :") ; Lire (l) ;
S
ß L x l ;
Écrire ("La surface du rectangle est :", S) ;
FinAlgo
EXERCICE III :
1.
|
Objet |
Type/Nature |
Rôle |
|
g |
Constante=9,8 |
Intensité de la pesanteur |
|
m |
Réel |
Masse de l’objet |
|
K |
Réel |
Raideur du ressort |
|
Δl |
Réel |
Allongement du ressort |
2. Const g=9,8 ;
Var m, k, Δl:
reels;
3. Algorithme AllongementRessort
Const g=9,8 ;
Var
m, k, Δl: réels;
Début
Ecrire (“Donner la valeur de la
masse m:”), Lire(m) ;
Ecrire (‘’Donner la valeur de la
raideur K : ‘’), Lire(K) ;
Δl ← m*g/K ;
Ecrire (‘’ L’allongement du
ressort est : ‘’, Δl) ;
Fin
EXERCICES IV
1.Algorithme SurfaceCercle
Const Pi =
3,14 ;
Var R, S : réels ;
Début
LIRE
(R) ;
S
← R*R*Pi ;
ECRIRE (’’La surface de ce cercle
est ‘’: S) ;
Fin
2.Algorithme ElèveAuCarré
Var unNombre, sonCarré :
entiers ;
Début
Ecrire
(‘’ Quel nombre voulez-vous élever au carré ? ‘’) ;
Lire (unNombre) ;
Son Carré ← unNombre*unNombre ;
Ecrire (‘’ Le carré de ‘’, unNombre) ;
Ecrire (‘’ c’est ‘’, sonCarré) ;
Fin
2. Algorithme
FaitLeTotal
Var nbVal, cpt : entiers ;
Valeur, totalValeurs : réels ;
Début
Ecrire
(‘’ Combien de valeurs voulez-vous saisir ? ‘’) ;
Lire
(nbVal) ;
totalValeurs ← 0 ;
Pour
cpt ← 1 à nbVal Faire
Ecrire
(‘’ Donnez une valeur ‘’) ;
Lire (valeur) ;
totalValeurs ← totalValeurs + valeur ;
Fin
Pour
Ecrire
(‘’Le total des », nbVal, »valeurs
est ‘’) ;
Fin
3-Algorithme ParExemple
Constante : (TVA : réel) ← 20,6 ;
(titre :
chaine) ← Resultat ;
Variable prix HT, prixTTC :
réels ;
Début
Ecrire
(‘’ Donnez-moi le prix hors taxes ; ‘’) ;
Lire
(prixHT) ;
prixTTC ← prixHT*(1+ TVA/100);
Ecrire
(titre) ;
Ecrire
(prixHT,”FCFA HT devient”, prixTTC,
“euros TTC) ;
Fin
4.Algorithme DivisionEuclidienne
// Cet algorithme permet de calculer puis d’afficher le
quotient et le reste de la division
Euclidienne de deux variables A par B //
Variables A, B : entiers ;
Début
Ecrire ("A = "),
Lire(A) ;
Ecrire ("B = "), Lire(B) ;
q← A DIV B
r← A MOD B
Ecrire (« Le quotient est ", q,
" et le reste est ", r)
Fin


