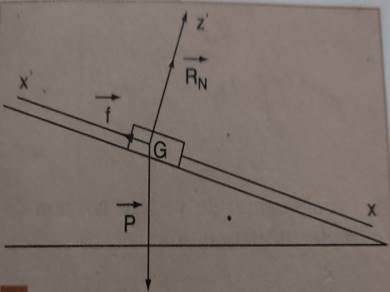
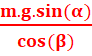MOUVEMENT D’UN SOLIDE SUR UN PLAN INCLINE

Un mobile (S) de masse m glisse sur un plan incliné d’un angle par rapport au plan horizontal.

Bilan des forces :

Poids du mobile(S), applique au centre de gravite de (S), de direction verticale.

: Réaction du plan, applique sur la surface de contact entre le plan et le mobile(S).

)

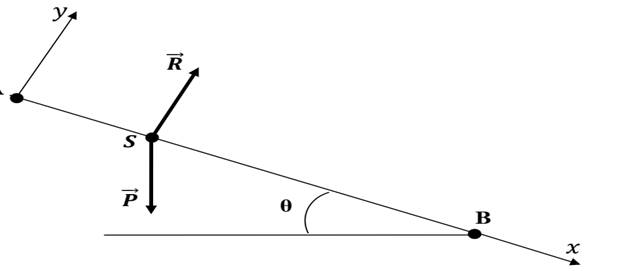
On considère les deux axes x et y :

 : a pour direction y

n’a pour direction ni x, ni y. Mais on peut décomposer le poids en deux composantes P_x suivant l’axe des x et P_y suivant l’axe des y.

P_x =Psin

P_y =Pcos

sin

Deux cas peuvent se présenter :

a- Les frottements sont négligeables

est normale au plan. D’après le TCI : · La projection sur l’axe des x donne : mgsinα =max soit : a=gsinα a est constante =>le mouvement est rectiligne uniformément accéléré. · La projection sur l’axe des y donne : -mgcosα +R=0 => R = mgcosα

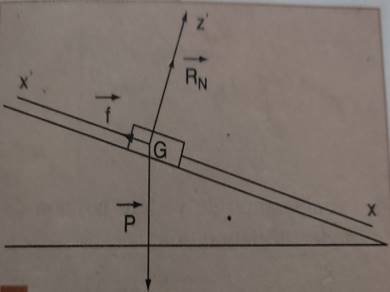
b-Les frottements ne sont pas négligeables

La force de frottement, colinéaire au vecteur vitesse et de sens opposé est notée. La réaction du plan n’est plus perpendiculaire à ce dernier, mais orientée vers l’arrière.

-la composante normale de y est notée

-la composante x est la force de frottement . On a :

D’après le TCI On obtient := · La projection sur l’axe des x donne : mgsinα +0+ – f =max soit : a=gsinα - a est constante =>le mouvement est rectiligne uniformément accéléré. · La projection sur l’axe des y donne : -mgcosα +RN+0=0 => RN=mgcosα Par la suite : R^2=RN^2+f^2

EXERCICES

EXERCICE I:
Une automobile de masse m = 1500 kg monte une côte de pente 5% à une vitesse v = 90 km.h-1.

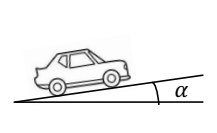
L’ensemble des frottements équivaut à une force unique opposée à , d’intensité f = 800 N. Soit la
force motrice de l’automobile. On prendra g=9,80 N/kg.
1. Calculer F_m

2. Calculer la puissance de P, appelée puissance du moteur.

3-Calculer le moment du couple moteur s’il tourne à 3000tr/mn

EXERCICE II:

Un véhicule, de masse m=1300kg, roule à vitesse constante V=90 km.h^-1 sur une route rectiligne et horizontale. L'ensemble des
forces s'opposant à l'avancement est équivalent à une force unique, opposée au vecteur vitesse, de valeur f=800N.
1. Déterminer la valeur de la force motrice développée par le moteur.
2. Le véhicule aborde, à présent, une côte formant un angle de 14,0° avec l'horizontale. Quelle doit être la nouvelle valeur de la force motrice si le conducteur maintient la même vitesse et que l'ensemble des forces s'opposant à l'avancement est toujours équivalent à une force unique, opposée au vecteur vitesse, de valeur f=800N ?

EXERCICE III:

Un solide de masse m=40 kg, abandonné sans vitesse initiale, glisse en translation le long de la plus grande pente d’un plan incliné faisant un angle =30° avec l’horizontale sous la seule action de son poids.

1. Calculer l’accélération du solide.

2. Quelle est la nature du mouvement

3. Donner l’équation horaire du mouvement de ce solide.

4. Au bout de 5 s, il atteint le bas de la pente. Calculer la vitesse au bas de cette pente.

5. Calculer l’intensité de la réaction R du plancher. On prendra g=9,80 ms^-2.

EXERCICE IV:

Soit un système (S, S’, poulie) ci-dessous :

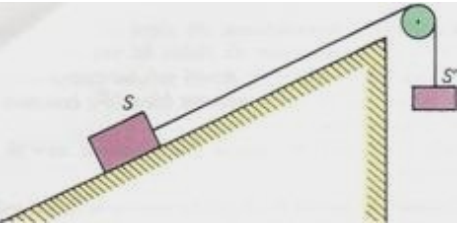
1. Représenter toutes les forces qui s’exercent sur les différentes parties du système (les forces de frottement et le poids de la poulie sont négligeables)

2. Calculer M_S en fonction de M_S’ et quand le système est en équilibres.

3. Calculer. L’accélération du système si M_S=100g, M_S’=75kg et =30°

4. Calculer la tension du fil

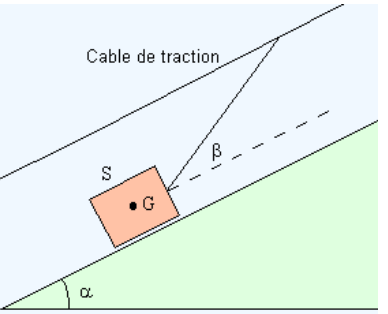
EXERCICE V:
Un bûcheron descend d’un traîneau remplis de bois sur un plan incliné d’un angle α = 20° par rapport à l’horizontale. La masse totale du traîneau est m = 400 kg. L’ensemble des frottements sur le traîneau équivaut à une force unique constante f = 500 N. La force exercée par le bûcheron est supposée parallèle au plan incliné. On prendra g=10 N/kg
1. Représenter les forces qui s’exercent sur le traîneau maintenu en équilibre.

2. Calculer leurs intensités. Le bûcheron descend le traîneau à vitesse constante.

3. Calculer les travaux des forces qui s’exercent sur le traîneau pour une descente d = 50 m. En déduire sa vitesse à la fin de ka pente.
4. La puissance moyenne de la force exercée par le bûcheron lors de ce déplacement est Pm = 75 W.

Calculer la durée du déplacement.

EXERCICE VI:

Un solide de masse m=5,00kg glisse sans frottement sur un plan incliné d'angle α=15,0° par rapport à l'horizontale. Il est entraîné à vitesse constante par un
câble faisant un angle β=20,0° avec la ligne de plus grande pente du plan incliné.

1. Déterminer la tension du fil de traction.
2. Déterminer la réaction du plan incliné.

RESOLUTION

EXERCICE I:

1. Calcul de F_m

1. système : l’auto

Bilan des forces :

: poids de l’auto
: réaction du plan
force de frottement
: la force motrice de l’auto.

2. Dans certains référentiels appelés référentiel galiléen, le centre d’inertie d’un solide isolé ou pseudo
isolé a un mouvement rectiligne uniforme s’il est en mouvement ou il reste au repos s’il est initialement
immobile.
𝑣 = 𝑐𝑡𝑒 ⟹

Suivant xx’ :F_m –f -mgsinα=0. =>F_m=f + mgsinα=800+ 1500x9,80 x=1535 N //on décompose le poids en deux composantes p_x=mgsinα et p_y=mgcosα

2. Calcul de P

P=Fv=1535x25=20735 W

3. Calcul du moment

P=M => M====66 Nm

EXERCICE II:

1. On étudie le système {véhicule} dans le référentiel terrestre
(supposé galiléen). Le système est soumis à 4 forces extérieures :
• Son poids :
• La réaction normale de la route :
• La force motrice :
• La force de frottements :

Le système est en mouvement rectiligne uniforme, donc d'après la première loi de Newton (principe d'inertie): +
On associe un repère au référentiel (voir schéma).

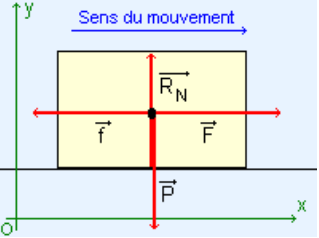
2. Projection sur ox:
F - f = 0 => F = f
Projection sur oy:
-P + R_N = 0 => P = R_N
La première équation donne immédiatement la solution:
F = f => F = 800N
2. On étudie le système {véhicule} dans le référentiel terrestre.
Le système est soumis à 4 forces extérieures. Ce système possède un mouvement
rectiligne uniforme. Le vecteur vitesse de son centre d'inertie est donc constant.
Principe d’inertie : +
On associe un repère au référentiel (voir schéma).

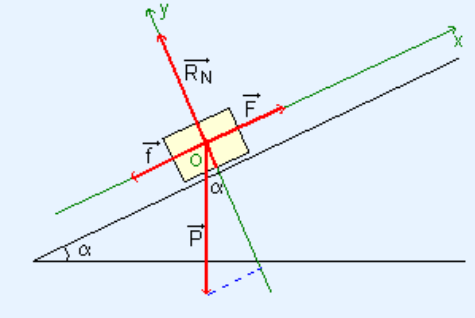
Projection sur ox:
-P.sin(α) + F - f = 0
Projection sur oy:
-P.cos(α) + RN = 0
La première équation donne immédiatement la solution:
F = f + m.g.sin(α) => F = 800 + 1300 x 9,81 x sin(14,0)
=> F = 3885,3N

EXERCICE III:

1. Accélération du solide.

D’après le TCI :

=m <=>

En projetant sur l’axe des x : mgsinα + 0=ma. => a=gsinα=9,8sin30=4,9 ms^-2.

2. Nature du mouvement

a=constante => le mouvement est uniformément varié.

3. Equations horaires.

=>= //à l’instant initial x₀=v₀=0

4. Vitesse au bas de cette pente.

Il aura parcouru : x=2,45(=61,25 m

On a : v²-v₀²=2a(x-x₀) =>v²=2ax=2x4,9x61,25 =600,25 => v=24,5m/s

5. Intensité de la réaction R du plancher.

En projetant sur l’axe des y :R-mgcosα=0 => R=mgcosα=40x9,8xcos30=339,48 N.

EXERCICE IV:

1.1 Un référentiel galiléen est un référentiel dans lequel le principe de l’inertie est vérifié.
1.2 Dans un référentiel galiléen, la somme vectorielle des forces extérieures appliquées à un solide est égale
au produit de la masse de ce solide par le vecteur-accélération de son centre d’inertie.
2. Système : le solide.
Référentiel d’étude : Référentiel terrestre supposé galiléen.
Bilan des forces :

𝑃⃗ : Poids du solide ;
𝑅⃗ : Réaction de la piste ;
Représentation des forces.

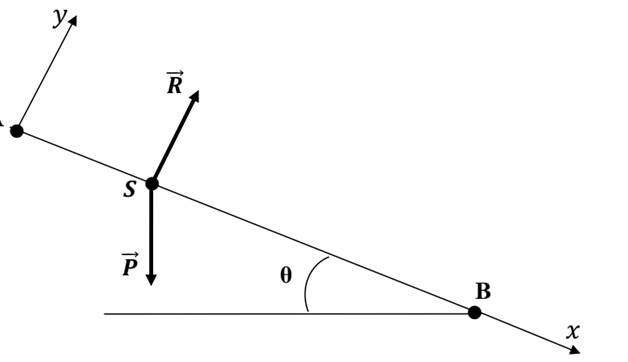
3. Appliquons le théorème du centre d’inertie au solide S.
𝑅⃗ + 𝑃⃗ = m.𝑎
Projection de cette relation vectorielle sur l’axe (A, x) :
R_x + P_x = ma_x
0 + m.g.sinθ = m𝑎_𝑥 d’où 𝑎_𝑥= g.sinθ
Le calcul donne 𝑎_𝑥= 10×sin30° = 5 m.s^–2
4. Détermination de V_B :
Appliquons le théorème de l’énergie cinétique au solide S entre les points A et B :
EC_B – EC_A = W (𝑃⃗) + W (𝑅⃗)
W(𝑅⃗ ) = 0 car 𝑅⃗ ⊥ (𝐴𝐵) ; W(𝑃⃗ ) = mglsinθ
EC_A = 0 car V_A = 0 et EC_B = 1/2𝑚𝑉_𝐵²
Le théorème devient 1/2𝑚𝑉_𝐵² = mglsinθ ; on tire 𝑉_𝐵 = √2𝑔𝑙𝑠𝑖𝑛𝜃
A.N : 𝑉𝐵 = √2´10´2´0,5 = 4,5m/s²

EXERCICE V:

1. Représentation des forces.

2. Calcul des intensités des forces.

P=mg=400x10=4000 N

R_N=P=mg=4000 N

R=4031 N.

F=f + mgsinα = 500 +400x10sin20=1868 N.

3. Calcul des travaux des forces qui s’exercent sur le traîneau pour une descente d = 50 m.

Travail du poids :68404 J

Travail de la force de frottements :-25000J

Travail de la force motrice :1868x50=93400J

Vitesse à la fin de la pente :

Théorème de l’énergie cinétique : <=>m

v===26,15 m/s
4. Durée du déplacement.

P= => t===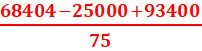1824s

EXERCICE VI:

On étudie le système {solide} dans le référentiel terrestre (supposé galiléen).
Le système est soumis à 3 forces extérieures :
• Son poids :
• La réaction normale du plan incliné :
• La tension du câble :

Le système possède un mouvement rectiligne uniforme. Le vecteur vitesse de son centre d'inertie est donc constant.
D'après le principe d’inertie :
Soit le repère associé au référentiel terrestre.
Projection sur ox:
-P.sin(α) + T.cos(β) = 0
Projection sur oy:
-P.cos(α) + R + T.sin(β) = 0
La première équation permet de déterminer la tension du câble:

T = => T=

=> T = 13,5 N.
2. La projection sur oy permet de déterminer la réaction du plan incliné :
R = m.g.cos(α) - T.sin(β) => R = 5,00 x 9,81 x cos(15,0) - 13,5 x sin(20,0)
=> R = 42,7 N