SOLIDE EN MOUVEMENT DE
TRANSLATION SUR UNE SURFACE PLANE ET HORIZONTALE
LOIS DE NEWTON SUR LE MOUVEMENT
Référentiels
Pour décrire
le mouvement d’un mobile, il est nécessaire de préciser un solide de
référence : C’est le référentiel.
Il existe plusieurs types de
référentiels :
- référentiel terrestre
- référentiel géocentrique
- référentiel héliocentrique
-
référentiel de Copernic
Forces extérieures et Forces intérieures
Les forces
extérieures sont des forces qui agissent sur les points du système et qui
proviennent des points étrangers au système.
Les forces intérieures sont les
forces qui agissent sur les points du système et qui proviennent d’autres
points appartenant à ce système.
Système isolé-système pseudo isolé
-Un système isolé est un solide
soumis à aucune force de la part de l’extérieur. Ce n’est pas possible car tout
objet est automatiquement soumis à une force gravitationnelle : sur la terre,
c’est le poids, dans l’espace ce sera l’attraction d’un autre astre.
-Un système est dit pseudo isolé lorsque la somme vectorielle des
forces qui lui sont appliquées est nulle.
Les lois de Newton
Première loi de Newton ou principe
d’inertie
Lorsque la
somme vectorielle des forces extérieures appliquées à un système est nulle, son
centre d’inertie est :
-Au repos si le système est
initialement au repos.
-Animé d’un mouvement rectiligne
uniforme si le système est initialement en mouvement.

Remarques :
-Un
référentiel dans lequel le principe de l’inertie est vérifié est dit galiléen.
– pour des expériences de laboratoire
usuelles, les référentiels terrestre, géocentrique et héliocentrique peuvent
être considérés comme galiléens.
– tout référentiel en translation rectiligne uniforme par rapport à un
référentiel galiléen est lui-même galiléen.
2ème loi de Newton ou relation
fondamentale de la dynamique
Dans un
référentiel galiléen : la résultante des forces exercées sur le système est
égale au produit de sa masse et du vecteur-accélération de son centre d’inertie
:

La deuxième loi est également
appelée Théorème du Centre d’Inertie
(TCI)
3ème loi de Newton ou principe des
actions réciproques
Si un système 𝐴 exerce une force sur un système 𝐵, alors
réciproquement, 𝐵 exerce sur 𝐴 une force de même valeur, même
direction mais de sens opposé. On peut écrire cette sous la forme mathématique
suivante :

SOLIDE
EN MOUVEMENT DE TRANSLATION
Un solide est en mouvement de
translation lorsque son centre de gravité se déplace d’un endroit à un autre.
Relation
fondamentale de la dynamique du solide en translation (RFD)
Dans un référentiel galiléen, la somme
vectorielle des forces extérieures appliquées à un solide est égale à la
dérivée par rapport au temps du vecteur quantité de mouvement de ce solide

![]()
![]() est la quantité de mouvement
du solide en kg.m/s
est la quantité de mouvement
du solide en kg.m/s

![]() est l’accélération du centre de gravité du solide en
m/s2
est l’accélération du centre de gravité du solide en
m/s2
m est la masse du solide en kg
Méthode de résolution
d’un problème de dynamique
-il
faut délimiter avec soin le système à étudier
-Choisir
le référentiel galiléen le plus approprié. Très souvent le référentiel de
laboratoire convient.
-
Faire le bilan des forces extérieures appliquées au système et schématiser ces
forces par des vecteurs.
-Ecrire
la relation traduisant le théorème du centre d’inertie dans le référentiel
galiléen considéré, cette relation étant directement inexploitable, la projeter
sur un système d’axes approprié.
Exemple :
Un
solide de masse m=120 Kg se déplace sur une route horizontale avec une
accélération a constante. L’ensemble des forces de frottements est équivalent à
une force unique de 600N. Calculer l’accélération ainsi que la réaction du sol.
On prendra g=10N/kg.
Le
système étudié est le solide.
Le
référentiel galiléen approprié est le référentiel de laboratoire
![]()
![]()
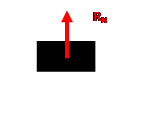
 Bilan des forces :
Bilan des forces :
![]() : Poids du solide
: Poids du solide
![]() Réaction du sol
Réaction du sol
D’après
le théorème du centre d’inertie :
![]()
![]()

![]()
![]() En projetant cette relation sur l’axe
horizontal :
En projetant cette relation sur l’axe
horizontal :
0
+Rx = max <=> 0 +f=max =>ax=f/m=600/120=5 m.s-2.
En
projetant cette relation sur l’axe vertical :
Ry=P=mg=120x10=1200N
R2
= Rx2 +Ry2 =>R=1342N
EXERCICES
EXERCICE I :
Une voiture de 1t roule à la vitesse de 90 km/h
sur une route rectiligne et horizontale. La puissance développée par le moteur
est 7,5 kw.
1.
Calculer l’intensité de la force motrice.
2.
Quelle est la nature du mouvement de cette voiture ?
3.
Donner l’équation du mouvement de cette voiture.
EXERCICE II :
Un solide de 50kg, initialement au repos, se
déplace sur une table rectiligne et horizontale d’un point A vers un point B.
Il est entraîné par une force de 150 N. On suppose les frottements
négligeables.
1.
Faire le bilan de toutes les forces et les représenter.
2.
Calculer l’accélération prise par le solide.
3.
Ecrire les équations horaires du mouvement.
4.Quelle
sera la vitesse du mobile après 150 m de distance parcourue ?
EXERCICE III :
Un solide de masse m=100kg initialement au
repos est mis en mouvement sur un plan horizontal par une force d’intensité F.
Les frottements sont équivalents à une force d’intensité f=100N.
1.Faire
un schéma avec inventaire des forces
2.
Calculer l’intensité de la force motrice sachant que a=2m.s-2.
3.
Calculer l’intensité de la réaction du plancher. On donne g=10ms-1.
EXERCICE IV :
Un observateur A de masse m=70 kg est debout
sur un pèse-personne installé dans un ascenseur en mouvement ascendant. La
montée de l’ascenseur comporte trois phases.
La
première phase est un mouvement uniformément accéléré d’accélération a=0,5 m.s-2.
La
deuxième phase est un mouvement rectiligne uniforme.
La
troisième phase est un mouvement uniformément retardé d’accélération a=0,4 m.s-2.
1.
Quel poids peut-on lire sur la balance pendant les trois phases.
2.
Interpréter alors se l’expression « poids apparent «
EXERCICE V :
Un mobile
autoporteur A de masse mA=650g et relié par un fil inextensible à un
solide B de masse mB=200g (montage
ci-dessous).

1. La soufflerie du moteur est arrêtée et le
mobile A est immobile.
a.
Déterminer la force exercée par le fil sur le solide B.
b.
Sachant que les forces exercées par le fil sur les solides A (T2) et
B (T1) ont même valeur, déterminer la valeur de la force de
frottement
exercée par la table sur le mobile A.
2.
La soufflerie du mobile A est maintenant en fonction. Le mobile A se met en
mouvement et glisse sans frottement sur la
table.
a.
Calculer la valeur de l’accélération prise par le système.
b.
En déduire la nature du mouvement.
RESOLUTIONS :
EXERCICE
I :
1. Intensité de force motrice
P=Fv => F=7500/25=300N //P=W/t=Fxd/t=F.v
2. Nature du mouvement de cette voiture.
v est constante donc le mouvement est
rectiligne uniforme.
3. Equation du mouvement de cette voiture.
x=vt +x0 or x0=0 donc x=25t //v=90000/3600=25 m/s
EXERCICE II :
1.
Schéma avec inventaire des forces

![]() Poids du solide
Poids du solide
![]() Force motrice
Force motrice
![]() : réaction du sol
: réaction du sol
2. D’après le théorème du centre d’inertie (TCI) :
![]()
![]() +
+![]()
![]()
Suivant l’axe des x :
F=ma =>a=![]() =3ms-2.
=3ms-2.
a=constante =>Le
mouvement est uniformément varié donc
3. Les équations horaires du mouvement sont :
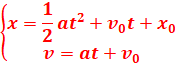
Le solide est initialement au repos =>: ![]()
Les équations deviennent :
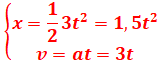
4. la relation
indépendante du temps entre les vitesses et les abscisses :
![]()
![]() =30m/s
=30m/s
EXERCICE
III :
1. Schéma avec inventaire des forces

![]() Poids du solide
Poids du solide
![]() Force motrice
Force motrice
![]() Forces de frottement
Forces de frottement
![]() : Réaction normale du sol
: Réaction normale du sol
2. Intensité de la force motrice.
D’après le théorème du centre d’inertie (TCI) :
![]()
![]() +
+![]()
![]()
Projection sur ox:
![]() ma => F=ma +
f=100x2+100=300N.
ma => F=ma +
f=100x2+100=300N.
3. Intensité de la réaction du plancher.
Projection sur oy:
P-RN=0 => RN=P=mg=100x10=1000N.
EXERCICE IV :
1. soit Pa, le poids apparent lu sur la balance. Le théorème du centre d’inertie
donne :![]()
en projetant suivant l’axe vertical, on a :
Première phase : -P+Pa=ma => Pa=ma +mg=m(a+g)=70(0,5+10)=735
N soit une masse de ![]()
Deuxième phase :Pa=P=mg=700N soit la
masse de ![]()
Troisième phase : -P+Pa=-ma => Pa=70(-0,4+10)=672 N soit une masse de ![]()
2. C’est la réaction de la balance qui provoque un poids fictif.
// Le poids
apparent est la force mesurée par la balance.
- Il dépend du
mouvement de l’ascenseur.
- C’est la
force de réaction normale du support.
- Si
l'ascenseur accélère vers le haut, le poids apparent augmente.
- S’il
ralentit en montant (ou accélère vers le bas), le poids apparent diminue.
EXERCICE V :
1. a. On étudie le système {B} dans le référentiel terrestre
(galiléen par approximation). {B} est soumis à deux forces de la
part du milieu extérieur :
• Son poids :
• La tension du fil T1:
Le système est en équilibre. D'après la première loi de Newton : ![]() =
= ![]() . On projette cette relation dans un
. On projette cette relation dans un
repère associé au référentiel terrestre (voir schéma).

Projection sur oy:
-P
+ T1 = 0 => T1 = P
=> T1 = mB.g
=> T1 = 200.10-3 x 9,81
=> T1 = 1,96N
b.
On étudie maintenant le système {A} dans le référentiel terrestre. {A} est
soumis à quatre forces :
• Son poids :
• La réaction normale du support :
• La force de frottement :
• La tension du fil ![]()
2:
Le système est en équilibre. D'après la première loi de Newton :
![]()
![]()
![]() =
=![]() .
.
On projette cette relation
dans un repère associé au référentiel terrestre (voir schéma).
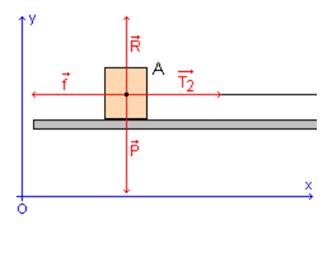
Projection
sur ox:
-f
+ T2 = 0 => f = T2
Or
T1=T2 car les forces exercées par le fil sur les solides
A et B ont même valeur, d'où:
f = T1 => f = 1,96N
2.
a. ![]()
![]() =
=![]()
![]()
Projection sur oy:
T1-P=mBa
![]()
![]() +
+![]() +
+ ![]() =
=![]() //le
mobile glisse sans frottements (f=0).
//le
mobile glisse sans frottements (f=0).
Projection sur ox:
<=> T2 =mAa . . .
![]()
T1=T2 => mB+
mBa= mAa
<=> a= 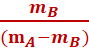 =
=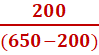 =0,44 ms-2.
=0,44 ms-2.
b. a=constante =>le mouvement est uniformément varié.
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire