MACHINES SIMPLES

Leviers
Un levier est un solide très rigide mobile autour d’un point appelé point d’appui.

Il existe 3 types de leviers :

1) Les objets dont le pivot est au milieu à inter-appui

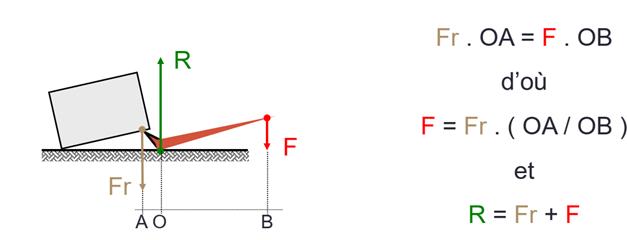
2) Les objets dont la charge est au milieu à inter-résistant

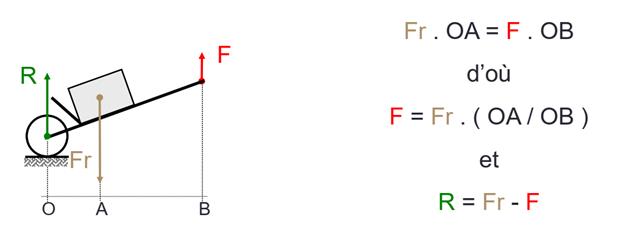
Applications : brouette, cisaille à levier, casse noix.

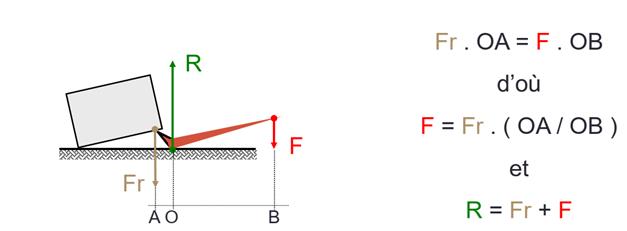
Applications : barre à mine, pied de biche
3) Les objets dont l’effort / la force est au milieu à inter-moteur

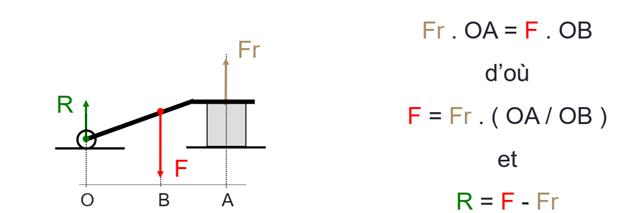
Applications : étaux à chaud, brucelles, pince à épiler…

Poulies
Une poulie est un disque libre de tourner autour d’un axe passant par son centre et supporté par une fourche appelée « chape ». Elle présente sur sa tranche une rainure appelée «gorge ». Les poulies permettent de soulever plus facilement une masse importante …).La poulie peut être « fixe » ou mobile.

Poulie appelée « fixe » (toujours à la même distance de son point d’attache)

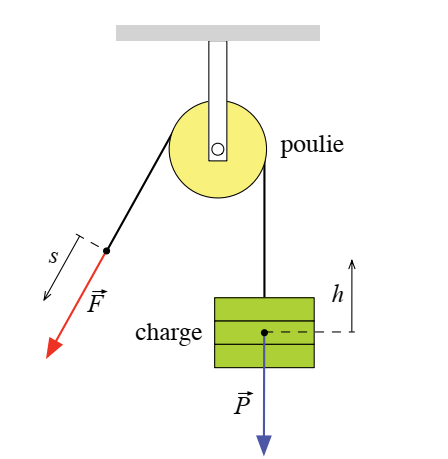
si la force motrice est et la force résistante est alors :

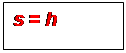Zone de Texte: s = h Pour monter la charge d’une hauteur h, nous devons déplacer le point d’application de la force F d’une distance s égale à la hauteur :

Poulie mobile

La charge à soulever est alors attachée à la chape de la poulie. L’une des extrémités de la corde est fixée à un point fixe et l’autre permet d’exercer la force motrice.

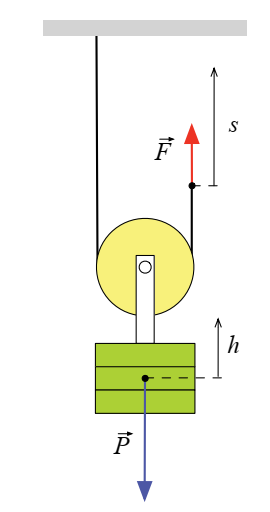
Si la force motrice est et la force résistante est alors

Pour monter la charge d’une hauteur h, nous devons déplacer le point d’application de la force F d’une distance s égale au double de la hauteur :
s = 2 h

Palans

Un palan résulte de la combinaison de plusieurs poulies.

Palan simple ou palan à deux brins (ou à deux poulies)

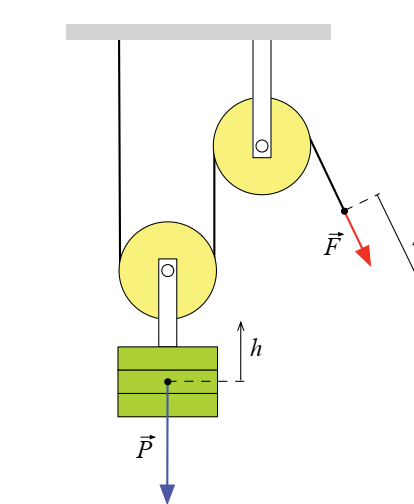
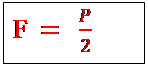Zone de Texte: F = P/2 si la force motrice est et la force résistante est alors

Palan à n brins

Pour un palan à n brins, si la force motrice est et la force résistante est alors

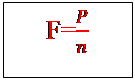
Zone de Texte: F=P/n

Lorsque la charge monte d’une hauteur h, chacun des N brins de la corde est raccourci de h, c’est-à-dire qu’il faudra tirer une longueur totale de corde de N h. La force F est donc appliquée sur la distance :
s = N h

Poulie à deux gorges

L’effort à fournir par l’opérateur est d’autant plus petit sue le rayon de la grande gorge R est grand devant le rayon r de la petite gorge.

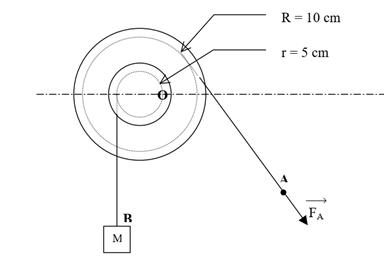
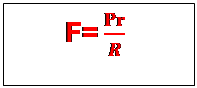Zone de Texte: F= Pr/R Pr=FR. =>.

Treuil

La force motrice à exercer est d’autant plus faible que la longueur du bras de la manivelle est grande devant le rayon du tambour. On a :

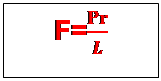Zone de Texte: F=Pr/L FL=Pr =>.

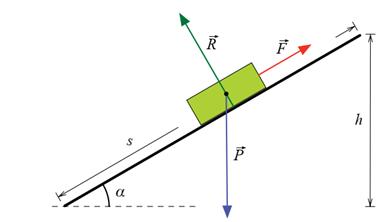
Plan incliné

Un plan incliné est une surface plane dont l’une des extrémités est plus élevée que l’autre, comme une bascule fabriquée à partir d’une longue pièce de bois posée sur une pièce d’appui. Une colline et une cage d’escaliers sont également des plans inclinés. Il est possible qu’on ait autrefois utilisé des plans inclinés pour déplacer de grosses pierres ou aider à construire des structures anciennes telles que les pyramides.

Inconvénients et avantages des machines simples

Machines simples	Avantages	Inconvénients
Plan incliné	Réduit l’effort à fournir	La distance à parcourir est plus grande
Poulie fixe	Diminution des efforts à fournir	-Ne diminue pas la force motrice -Usure de la corde ou du câble
Poulie à deux gorges	Diminution des efforts à fournir	-La longueur de la corde tirée est plus grande que le déplacement de la charge. -Usure de la corde
Palan à 4 brins	-diminue l’effort à fournir -permet de tirer du haut vers le bas	-longueur de la corde tirée très grande par rapport au déplacement de la charge -encombrant -coût élevé
Treuil	Réduit l’effort à fournir	-Usure de la corde -stabilisation difficile du dispositif

EXERCICES

EXERCICE I

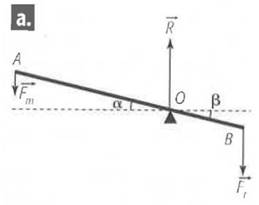
Pour soulever une pierre de forme cubique, on utilise un levier AOB. OA=1,20m, OB=20cm, F_r=900N.

1. Quelle force verticale faut-il appliquer en A ?

2. Quelle est la réaction du couteau en O ?

EXERCICE II

1 Quelle devrait être la longueur du bras de levier résistant permettant de soulever une masse de 13 g à partir d’une force motrice de 0,0294 N si le bras de levier moteur de ce levier inter-résistant est d’une longueur de 12 cm?

2 Quelle est la longueur de planche minimale nécessaire à la conception d’un levier inter-résistant capable de soulever une masse de 200 g avec une force de 0,196 N et d’un bras de levier résistant de 8 cm ?

3 Un levier inter-appui est constitué d’un point d’appui et d’une planche de 100 cm de longueur. On dispose le point d’appui sous la planche de façon à ce que l’avantage mécanique de ce levier soit de 3. Quelle sera la longueur du bras de levier résistant? On prendra g=9,8N/kg.

EXERCICE III

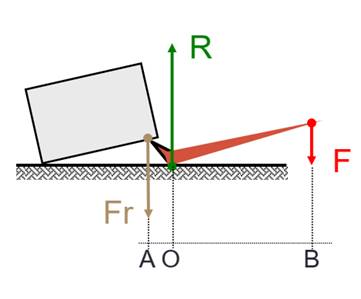
Un pied de biche est un levier coudé AOB utilisé pour arracher des clous. On négligera son poids et on considérera qu’il peut tourner sans frottements autour du point d’appui O .Le levier est équilibré. OB est perpendiculaire à OA. OA= 3cm, OB=30cm

1- On exerce à l’extrémité de B une force perpendiculairement à OB. Le clou est arraché avec une force d’intensité 1500N. Calculer l’intensité de .

2- Ecrire la relation entre les différentes forces appliquées au levier. En déduire la réaction de la planche en O.

EXERCICE IV:

Quelle devrait être la longueur d’une manivelle permettant de soulever une masse de 20 kg à
l’aide d’un treuil dont le tambour a un diamètre de 20 cm, si on applique une force motrice
de 25 N?

EXERCICE V :

Un mobile de masse m=50 kg est maintenu en équilibre sur un plan incliné d’un angle de 30° par rapport à l’horizontale.

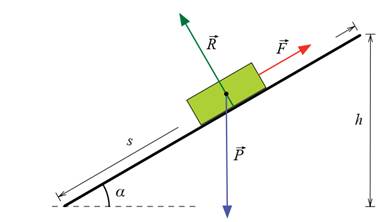
1. Calculer l’intensité de la force F qui le maintien en équilibre. on prendra g=10N/kg

2. Calculer la réaction R.

EXERCICE VI :

Un solide (S) de masse 36000g est maintenu en équilibre par un ressort (R) accroché au point A. Le plan est incliné d’un angle de 30° par rapport au plan horizontal. On donne g=10 N/Kg

1-Représenter les forces en présence sur un schéma

2-Calculer la tension du ressort et la réaction du plan incliné.

3-En déduire la constante de raideur de ce ressort si l’allongement est 20 cm.

EXERCICE VII:

1.1-On considère un système constitué de deux masses A et B relié par un fil inextensible et sans masse, passant par la gorge d’une poulie de masse négligeable. Le système (A, B, poulie) est en équilibre. On néglige les frottements.

1.1.1-Représenter toutes les forces qui agissent sur les différentes parties du système.

1.1.2-Calculer l’intensité de la tension en A ainsi que la réaction du plan.

1.1.3-Calculer la masse m_B. On donne : m_A=300g ;α =30° ; g=10N/Kg

1.2-On intercale entre M et B, un ressort à spires non jointives, la masse B provoque un allongement de 5 cm.

1.2.1-Calculer la raideur du ressort en supposant que le système est de nouveau en équilibre

1.2.2-On remplace la masse B par un récipient cylindrique en matière plastique très légère dont la masse est négligeable par apport a la masse d’eau qu’il contient. Calculer la hauteur de l’eau dans le récipient quand le système est en équilibre. On donne : section intérieure du récipient S=20cm² ; masse volumique de l’eau ρ₀ =1000 kg.m^-3; g=10 N/kg

CORRIGES:

EXERCICE I

1. F_r.OA=F_m.OB =>