SYSTEME DE DEUX EQUATIONS ET INEQUATIONS A DEUX INCONNUES DANS IRXIR

SYSTEME D’EQUATION

Définition

On appelle système linéaire de deux équations dansIR²tout système de deux équations de premier degré de la forme:

Résoudre un système linéaire de deux équations à deux inconnues dans IRXIR revient à déterminer les couples(x, y) solution de ce système,

La résolution d’un tel système se fait par substitution, combinaison, graphiquement et par la méthode de Cramer.

a) Méthode du déterminant (ou méthode de Cramer)
Pour résoudre le système linéaire de deux équations de premier degré dans IR en utilisant la méthode du déterminant, on procède comme suit:

· On calcule le déterminant principal

· On calcule ensuite le déterminant en x , Δx

· On calcule ensuite le déterminant en y , Δy

Les solutions du système sont:

Exemple: Soit à résoudre le système

Δ==(2)(5)-(3)(3)=10-9=1

Δx==(5)(5)-(7)(3)=25-21=4

Δy==(2)(7)-(3)(5)=14-15=-1

x=Δx/Δ=4/1=4

y=Δy/Δ=-1/1=-1

b) Méthode par substitution
On procède comme suit :
-Dans l’une des équations, on exprime l’une des inconnues en fonction de la deuxième
-On remplace dans l’autre équation cette inconnue par son expression déterminée plus
haut, puis on résout cette équation à une inconnue pour trouver la valeur de la deuxième inconnue.
-On remplace cette deuxième inconnue par sa valeur dans l’expression de la première afin de trouver aussi la valeur de la première inconnue.

Exemple:Résoudre dans IR

Résolution:

De la première équation y=(1-2x)/3

On remplace y par cette expression dans la deuxième équation

< = > 4x-5((1-2x) /3) =2

< = > 4x –5/3 +10x/3=2

< = >22x/3=11/3

=> x=11/22=1/2

On peut trouver y en remplaçant x par

y=(1-2x)/3y=(1-2(1/2)/3=0 =>S={(1/2,0)}

c) Méthode par combinaisonlinéaire

Elle consiste à multiplier chacune des deux équationspar des coefficients appropriésde façon àéliminerune des deux variables et à déterminer l’autre par la suite.

Exemple:Résoudredans IR

Multiplions la première équation par 3 et la seconde par 2, on a:

En faisant l’addition membre à membre, on obtient:

0x +y= -1=> y=-1

On remplace y par-1dans l’une des deux équations:

=> x=-2

S={(-2,-1)}

SYSTEME D’INEQUATION

Pour représenter l’ensemble des points dont les coordonnées sont solutions d’un système d’inéquations du 1er degré dans IR×IR, on procède comme suit :
-On représente d’une couleur l’ensemble des points dont les coordonnées sont
solutions de la première inéquation
-On représente d’une autre couleur l’ensemble des points dont les coordonnées
sont solutions de la deuxième inéquation
-L’ensemble solution du système d’inéquation est la partie du plan où l’on
retrouve les hachures des deux couleurs
Remarque
La résolution d’une inéquation ou d’un système d’inéquation se fait par méthode graphique

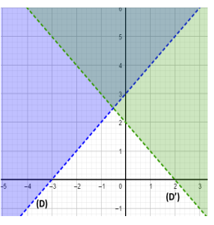
Exemple: Résoudre graphiquement le système:

Soient les droites (D) et (D’) d’équations respectives x-y+3=0 et x+-2=y=0.

On trace, dans un même repère, (D) et (D’), on hachure les demi-plans qui correspondent aux solutions de chaque équation.

L’ensemble des solutions est la partie hachurée deux fois (en bleu et en vert).

EXERCICES

EXERCICE I: Résoudre par substitution, par combinaison linéaire et par déterminant le système suivantdans IRxIR:

EXERCICE II :

1.Resoudre dans IR² les systèmes suivants:

2. Résoudre dans IR² les systèmes suivants:

3. Utiliser les auxiliaires pour résoudre dans IR² les systèmes suivants:

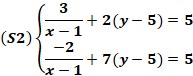
EXERCICE III:

Soient x et y deux réels vérifiant xy = 48 et x² + y² = 100.
1. Montre que le couple (x; y) est solution des systèmes suivants : (S1) :

2. Résous dans IR² en utilisant la substitution les systèmes (S1) et (S2)

EXERCICE IV : Résoudre dans IR³

1. Derrière la palissade, il y a des kangourous et des rhinocéros. J’ai compté 78 pattes et 54 oreilles. Combien y a-t-il d’animaux de chaque espèce ?

2.Dans ma tirelire, j’ai des pièces de 2 Fr. et des pièces de 5 Fr. soit 15 pièces en tout. Combien ai-je de pièces de chaque sorte, sachant que j’ai 54 Fr. ?

3.Il y a 6 ans, Jean avait 4 fois l’âge de Marie. Dans 4 ans, Jean aura 2 fois l’âge de Marie. Quel âge ont-ils maintenant ?

EXERCICES V:

Détermine et représente graphiquement l’ensemble des solutions des systèmes:

1,

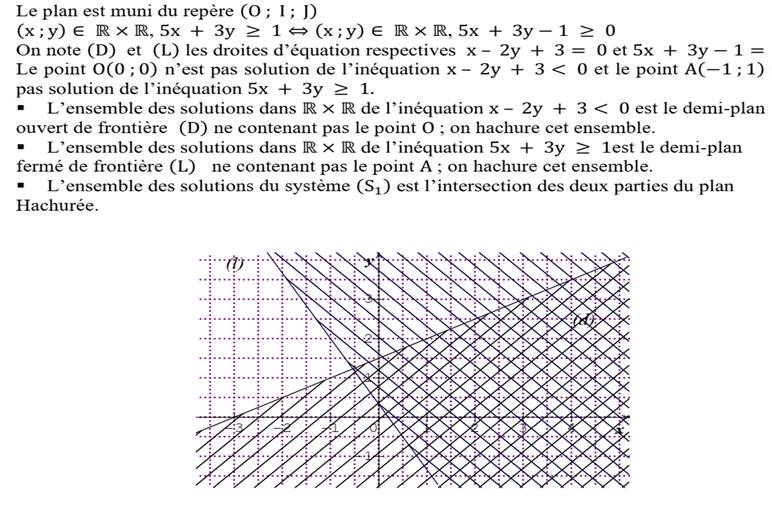
2.

Avez-vous un exercice à proposer au Forum?Cliquez-ici

CORRIGES

Merci de votre visite
Laissez un commentaire