MOUVEMENTS CIRCULAIRES (CINEMATIQUE)

PARAMETRES CINEMATIQUES DU MOUVEMENT

           Un mouvement est circulaire lorsque sa trajectoire est un cercle.

 

 

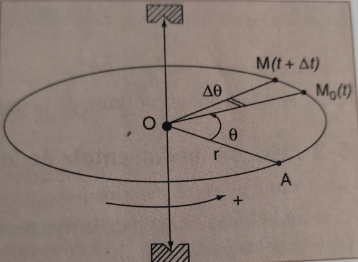
Soit un mobile M en mouvement circulaire autour d’un axe situé au point O. Sa projection est un cercle de centre O et de rayon r = OM.

 

Abscisse curviligne

Si le point M se déplace en décrivant l’arc de cercle MM0, sa position peut être déterminée par son abscisse curviligne :

 

 

 

Abscisse angulaire 

           La position du point M est aussi déterminée  à chaque instant par l’angle     ().

La valeur de l’angle

 

 θ = () 

 

est appelé abscisse angulaire du point M.

Le signe de θ est déterminé par le sens positif choisi (très souvent le sens trigonométrique)

 

La relation qui lie abscisse curviligne s et l’angle polaire θ est :

 

s=rθ  

        

 

Le mobile balaie un angle

 

 

 

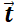
En un tour, l’angle balayé est :

 

 

En  n tours, l’angle balayé  est :

 

 

 

Si le mobile M fait n tours en t secondes sa vitesse de rotation sera :

 

  

N en tours par seconde (tr/s)

Vitesse linéaire

La vitesse linéaire a un instant t est égale a la dérivée de l’abscisse curviligne par rapport au temps :

 

 

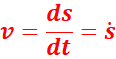
Vitesse angulaire

La vitesse angulaire est la dérivée de l’angle par rapport au temps :

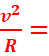
En fonction de la vitesse linéaire, la vitesse angulaire est donnée par la formule :

 

 

En onction de la vitesse de rotation, la vitesse angulaire est donnée par la formule :

 

 

Accélération angulaire

 

L’accélération angulaire instantanée, notée Ӫ, est la dérivée seconde par rapport au temps de l’abscisse angulaire :

 

 

 

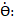
Unité : radian par seconde carré (rad/s2)

 La base de Frenet  () est une base liée au mobile et pour laquelle  est le vecteur unitaire pris sur la tangente orientée et    le vecteur perpendiculaire a     et oriente vers le centre de courbure de la trajectoire. Dans cette base, le vecteur accélération s’écrit :

 

 

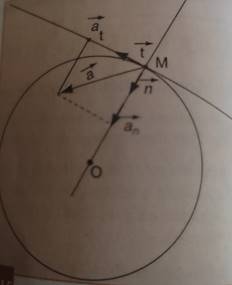
Les deux composantes du vecteur accélération d’un mouvement circulaire sont :

-Composante tangentielle :

 

 at  = RӪ

 

-Composante normale :    

 

 an = R2

 

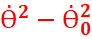
TYPES DE MOUVEMENTS

Mouvement circulaire uniforme

          Un Mouvement circulaire est dit uniforme si sa vitesse angulaire est constante ()

Equation horaire du mouvement :      

 

  

 

θ0 : élongation  initiale en radian (rad)

vitesse angulaire  en radian par seconde (rad/s)

θ: élongation à l’instant t quelconque (rad)

Période    

.     On appelle période d’un mouvement circulaire uniforme, la durée que met le mobile pour effectuer un tour complet. Elle se note T,

 

 

T en seconde (s)

Fréquence :                                                       

.       On appelle fréquence (f) du mouvement, le nombre de tours effectués pendant une seconde

        

f

f en hertz (hz)

 

Mouvement circulaire uniformément varié

Un Mouvement circulaire est dit uniformément varié si son accélération angulaire est constante ()

Equations horaires du mouvement :

 

 

 

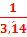
θ0 : élongation  initiale en radian (rad)

Vitesse angulaire en radian par seconde (rad/s)

Ӫ : accélération angulaire en radian par seconde carré(rad/s2)

θ: élongation à l’instant t quelconque (rad)

 

Relation indépendante du temps entre  et:

 

 

 

EXERCICES.

 

EXERCICE I :

             Un corps est animé d’un mouvement circulaire uniforme d’équation : Ѳ=2t +5  (rad)

1. Quelle est sa vitesse angulaire.

2. Quelle est la valeur de l’élongation à l’instant initial ?

3. Calculer la valeur de l’angle balayé après 60 mn.

4. Déterminer la fréquence et la période du mouvement

EXERCICE II :

Un disque de 45 tours tourne à la vitesse de 45 tr.mn-1

1. Quelle est la trajectoire d’un point M du disque situé à 10 cm de l’axe de rotation ?

2. Quelle est la nature du mouvement de M ?

3. Calculer la longueur de la trajectoire décrite par M lorsque le disque fait un tour ?

4. Quel est en ms-1 la vitesse de M ?

EXERCICE III :

            Un point M d’un cercle de rayon R=10cm effectue 10 trs en 2s.

1-    Déterminer l’angle balayé par le point M

2-    Déterminer la vitesse de rotation du mobile M

3-    Déterminer la vitesse angulaire du point M.

4-    Déterminer l’accélération tangentielle sachant que Ӫ=4rad/s2

5-    Déterminer l’accélération normale.

6-    Déterminer la période du mouvement

7-    Déterminer la fréquence du mouvement.

 EXERCICE IV :

On fait tourner un disque initialement au repos jusqu’à atteindre une vitesse de 8rad/s.

1.Quelle est la valeur de l’angle balayé par un rayon du disque au cours de ce mouvement si l’accélération vaut 2,5 rad/s ?

2.Lancé à cette vitesse, le disque s’arrête au bout de 2s. Calculer la nouvelle valeur de l’accélération.

.

 

CORRIGES

EXERCICE I :

1.Le mobile est animé d’un mouvement circulaire uniforme d’équation θ =t +θ0 ‘

2.Par identification, Sa vitesse angulaire est

Son élongation à l’instant initial est θ0 =5 rad

3. θ =t +θ0 ‘=2(60x60) + 5 =7205 rad

4. T== =3,14 s

f= = =0,31 hz

 

EXERCICE II:

1. C’est une trajectoire circulaire

2. c’est un mouvement circulaire uniforme

3.L=2πr=2x3,14x0,1=0,628m

4. ..

EXERCICE III :

1. Ѳ = 2πn=2x3,14x10=62,8 rad

2. N =n/t=10/2 =5 trs/s

3. =  2πN=2x3,14x5=31,4rad/s

4. at=RӪ=0,1x4=0,4m/s2

5. an = R2=0,1x(31,4)2=98,6m/s2

6.  =  =0,2 s

 

 EXERCICE IV :

1.    Equations horaires du mouvement :

2.    

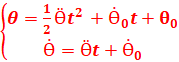
Relation indépendante du temps entre  et:

 (θ- θ0)

=> Relation indépendante du temps entre  et:

θ=> θ===12,8rad

2. =>-=-4rad/s2