MACHINES SIMPLES
Une machine simple est un dispositif comportant peu de pièces
qui permet de faciliter l’accomplissement d’un travail en réduisant les efforts
fournis,
Poulies
Une poulie est un disque libre de tourner autour d’un axe passant
par son centre et supporté par une fourche appelée « chape ». Elle présente sur
sa tranche une rainure appelée « gorge ». Les poulies permettent de soulever
plus facilement une masse importante …). La poulie peut être « fixe » ou mobile.
Poulie appelée «
fixe » (toujours à la même distance
de son point d’attache)
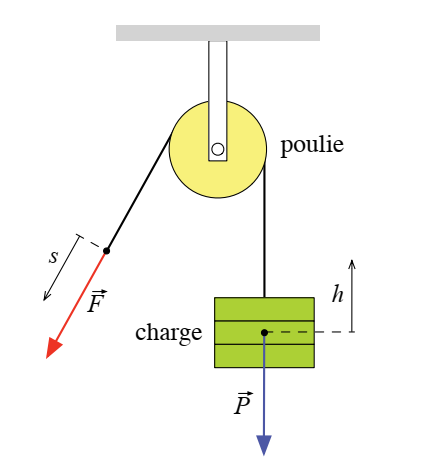
Si la force motrice est 
et la force résistante est 
alors :
F=P
Pour monter la charge d’une hauteur h,
Nous devons déplacer le point d’application de la force F d’une
distance s égale à la hauteur
:
s=h
Poulie mobile
La charge à soulever est alors attachée à la chape de la poulie. L’une des extrémités de la corde est fixée à un point fixe et l’autre permet d’exercer la force motrice.
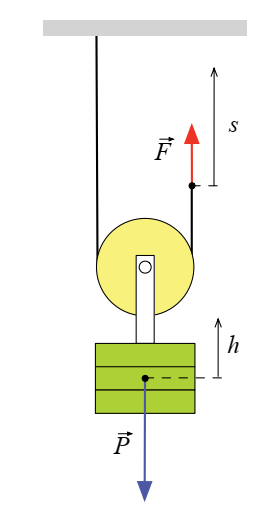
Si la force motrice est 
et la force résistante
est 
alors
F=P
Pour monter la charge
d’une hauteur h,
Nous devons déplacer le point d’application
de
la force F d’une distance s égale au double de la hauteur :
s = 2 h
Palans
Un
palan résulte de la combinaison de plusieurs poulies.
Palan simple ou palan à deux brins (ou à deux poulies)
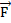
Si la force
motrice est 
et la force résistante est
alors :
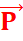
Palan à n brins
Pour un palan à n brins, si
la force motrice est
et la
force résistante est alors :
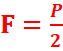
Lorsque la charge monte d’une hauteur h,
chacun des n brins de la corde est raccourci de h, c’est-à-dire
qu’il faudra tirer une longueur totale de corde de n h. La force F est
donc appliquée sur la distance :
s = n h
Poulie à deux
gorges
L’effort à fournir par l’opérateur est d’autant plus petit sue le
rayon de la grande gorge R est grand devant le rayon r de la petite gorge.
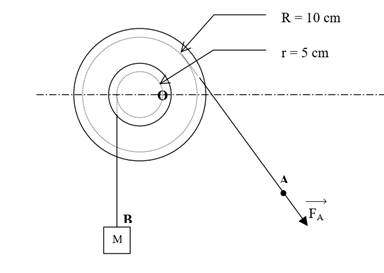
Pr=FR. =>
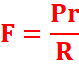
Treuil
La force motrice à exercer est d’autant plus faible que la
longueur du bras de la manivelle est grande devant le rayon du tambour.
On a :
FL=Pr =>
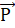
Plan incliné
Un plan incliné est une surface plane dont
l’une des extrémités est plus élevée que l’autre, comme une bascule fabriquée à
partir d’une longue pièce de bois posée sur une pièce d’appui. Une colline et
une cage d’escaliers sont également des plans inclinés. Il est possible qu’on
ait autrefois utilisé des plans inclinés pour déplacer de grosses pierres ou
aider à construire des structures anciennes telles que les pyramides.
F=Psinα
R=Pcosα
Inconvénients et avantages des machines
simples
|
Machines
simples |
Avantages
|
Inconvénients
|
|
Plan incliné |
Réduit l’effort à fournir |
La distance à parcourir est plus grande |
|
Poulie fixe |
Diminution des efforts à fournir |
-Ne diminue pas la force motrice -Usure de la corde ou du câble |
|
Poulie à deux gorges |
Diminution des efforts à fournir |
-La longueur de la corde tirée est plus grande que le
déplacement de la charge. -Usure de la corde |
|
Palan à 4 brins |
-diminue l’effort à fournir -permet de tirer du haut vers le bas |
-longueur de la corde tirée très grande par rapport au
déplacement de la charge -encombrant -coût élevé |
|
Treuil |
Réduit l’effort à fournir |
-Usure de la corde -stabilisation difficile du dispositif |
EXERCICES
EXERCICE I :
On utilise une poulie fixe pour soulever une charge de
masse 75 kg. La longueur de la corde tirée est 2,10m.
1. A quelle hauteur s’élève la charge ?
2. Quelle est l’intensité F de la force exercée pour
faire cette opération ?
3. On remplace cette poulie fixe par une poulie
mobile. Que devient la longueur de la corde tirée ?
EXERCICE II :
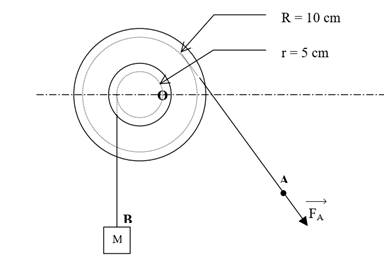
On considère un système de palan représenté par la
figure.
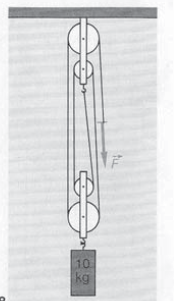
1. Calcule l’intensité du poids du solide sachant que
sa masse est M=10 kg et l’intensité de la pesanteur g=10N/kg
2. Quelle est l’intensité de la force motrice exercée
par l’opérateur ?
3. Quelle force obtiendrait-on si on avait un palan à
6 brins ?
EXERCICE III:
Pour soulever lentement une charge de 300kg dans un
garage, un ouvrier utilise une poulie à deux gorges.
On désigne par R le rayon de la grande gorge et par r
celui de la petite gorge.
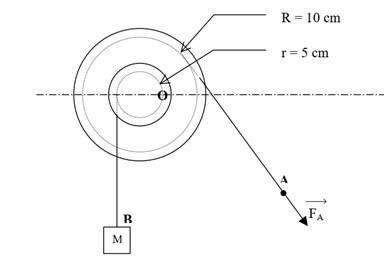
1. Calcule l’intensité F de la force motrice exercée
par l’ouvrier sachant que R=10 cm et r=5cm. On prendra g=10N/kg.
2. Quel doit être le rapport 
si pour soulever lentement cette
charge, l’ouvrier doit exercer une force
de 500N ?
EXERCICE IV :
On pose sur un plan incliné d’un angle ᵅ=45° par
rapport à l’horizontale une charge de de masse 50 kg.
1. Calculer l’intensité F de la force qui maintient la
charge en équilibre. (g=10N/kg)
2. Que se passerait –il si on diminue l’angle du plan
incliné ?
3. Quelle est l’intensité de la réaction du
plan ?
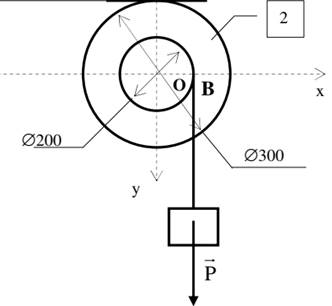
EXERCICE V :
Soit le treuil représenté par la figure
ci-dessous :
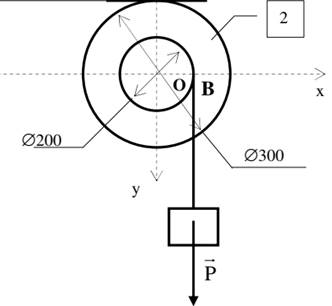
La charge a pour intensité 500N. La longueur de la
manivelle est 300mm et le rayon du tambour 200mm.
Quelle est la force F à appliquer sur la
manivelle ?
EXERCICE VI:
Dans un chantier de construction d’un
bâtiment, le manœuvre Ondoua doit faire monter une
charge de 150 kg du sol (rez de chaussée) au deuxième
étage. L’intensité maximale de la force musculaire qu’il peut exercer est 400
N. Après plusieurs essais, il n'arrive pas à soulever cette charge. En se
référant au chef chantier, celui-ci met à sa disposition les appareils de
levage suivants :
• Une poulie fixe ;
• Un palan à quatre brins ;
• Un treuil de rayon r = 30 cm, dont la longueur de la manivelle est L = 90 cm.
Biloa, le chef manœuvre suggère à Ondoua
d'utiliser une poulie fixe.
Autres informations :
Intensité du poids de la charge: P; intensité de la
force musculaire nécessaire : F; nombre de brins du palan :4.
|
Poulie
simple |
Palan
à n brins |
Treuil
(r, L) |
|
P=F |
F=Pn |
F=r×PL |
Donnée : g = 10 N/Kg
En utilisant les informations ci-dessus et en s’aidant d’une démarche
scientifique :
1. Examine la proposition de Biloa.
2. Aide Ondoua à choisir le dispositif le plus
adapté.
(BEPC 2022)
EXERCICE VII:
Dans le chantier d’un
immeuble en construction de votre papa, les ouvriers sont en train d’élever les
murs qui vont constituer le premier étage dont le plancher est à 4m au-dessus
du niveau du sol. Un manœuvre dont la masse totale est 45kg est prépose à leur
fournir du mortier (mélange de sable, de ciment et d’eau) à l’aide d’un seau,
lequel, rempli de mortier, a une masse totale de 50kg. Votre cadet qui a visité
le chantier vous dit que l’ouvrier n’utilisera ni l’escalier ni une échelle.
Il vous est alors demandé de proposer à l’ouvrier se trouvant au sol, un moyen
de faire monter le seau de mortier rempli à la hauteur voulue.
Tâche 1 : Identifier le problème qui se pose et proposer au
manœuvre trois appareils de levage qu’il pourra utiliser pour résoudre
celui-ci.
Tâche 2 : Expliquer pourquoi une poulie fixe ne peut être utilisée
pour résoudre ce problème.
Tâche3 : Décrire le mode opératoire pour que l’ouvrier fasse monter
le seau de mortier rempli avec l’appareil de levage que vous aurez choisi.
(Dresser la liste du matériel et expliquer en quelques mots comment l’utiliser.
Prendre : g = 10 N/kg
(EPREUVE ZERO 2023
NORD_OUEST)
CORRIGES
EXERCICE I :
1. Pour monter la charge d’une hauteur h,
nous devons déplacer le point d’application de la force F d’une distance
s égale à la hauteur :
s = h=2,10 m
2. F=P=75x9,81=825,75N
3.s=2h=2x2,1=4,2 m.
EXERCICE
II :
1. P=mg=10x10=100N
2.
F=P/4=100/4=25N
EXERCICE III:
1.
1 P=mg=300x10=3000N
Pr=FR =>F=Pr/R=3000x0,05/0,1=1500N
2. 
=
=
=
EXERCICE IV :
1. F=Psinα=mgsinα=50x10xsin45=353,55N
2. La force diminue.
3. R=mgcosα=50x10x0,707=353,5N.
EXERCICE V :
On a : FL=Pr
=>F=Pr/L=500x0.2/0,3=33,33N
Dans cette
tâche, il est question de vérifier si Ondoua peut
utiliser une poulie fixe pour monter une charge de 150 kg du sol (rez-de-chaussée ) au deuxième étage. Pour cela, nous allons :
• Déterminer l’intensité du poids de la charge afin d'en déduire l’intensité F
de la force à exercer pour soulever cette charge
• Comparer l’intensité de la force →F à l’intensité de la force
musculaire maximale −→Fm;
• Conclure.
Calcul de l’intensité du poids de la charge :
P=mg= 1500N
Comparaison du poids P de la charge l’intensité (le la force musculaire que
peut exercer Ondoua (Fm)
On constate que: F≻Fm car 1500N≻400N
Conclusion:
Ondoua ne peut pas soulever la charge avec une poulie
simple. Par conséquent, la proposition de Biloa à Ondoua n’est pas appropriée. ‘
Tâche 2
Dans cette tâche, il est question choisir parmi les appareils de levage le
dispositif le plus adapté pour soulever la charge.
Pour cela, nous allons :
• Déterminer l’intensité de la force →F à exercer dans chaque
cas ;
• Comparer l’intensité de cette force clans chaque cas à celle de la force
musculaire maximale ;
• Conclure.
1) Calcul de l’intensité de →F dans le cas du palan à 4 brins:
F1=mg4 =375N
2) Calcul de l’intensité de →F dans le cas du treuil:
F2=mgLr =500N
3) Cas de la poulie simple :
F3=150×10 =1500N
Comparaison : F2≻Fm, car 500N≻400N;
alors que F1≺Fm, car 375N≺400N
Donc l'appareil de levage à utiliser par Ondoua est
celui qui lui permettra d'exercer une force dont l'intensité est inférieure à
l'intensité maximale de sa force musculaire :
Ondoua doit utiliser le palan à 4 brins.