Durée : 100 minutes
PROPRIETE DE THALES
PROPRIETE DIRECTE DE THALES :
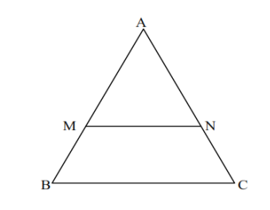
Soit ABC un triangle, M est un point de
la droite (AB) et N est un point de la droite (AC) tel que A, M et B soient
alignés dans le même ordre que A, N et C ; si les droites (MN) et (BC) sont parallèles
alors on a :
![]()
NB : Cette propriété permet
de calculer les longueurs
Exemple : les droites (EF) et (BC) étant parallèles, on donne AB=6, AE=2,
AC=9.Déterminons AF.
 .
.
(EF)//(BC) d’après la
propriété directe de THALES
,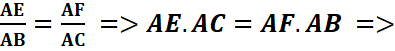

RECIPROQUE DE THALES
Soient ABC un triangle et N et M
deux points du plan tels que :
·
M ϵ à
la droite (AB) et N ϵ à la droite (AC).
·
Les points
A, M et B sont alignés dans le même ordre que les points A, N et C.
Si ![]() =
= ![]() alors les droites (MN) et (BC) sont
parallèles.
alors les droites (MN) et (BC) sont
parallèles.
Exemple : OQ=4 ; ON=2 ;
OM=3 et OP=6
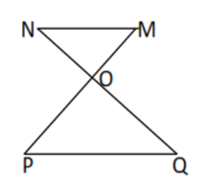
On
a :
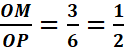

On constate
que : 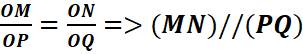
EXERCICES
EXERCICE I :
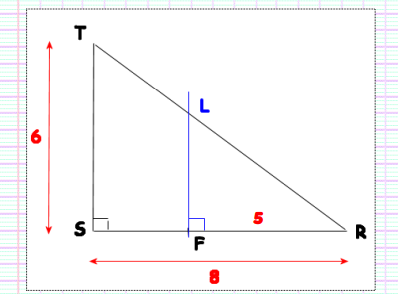
RST est un triangle rectangle en S tel que
RS=8cm et ST=6cm.
F est le point de (RS) tel que RF=5cm.
La droite perpendiculaire à la (RS) passant par
F coupe (RT) en L.
1. Les droites (ST)
et (LF) sont-elles parallèles ? Justifier.
2.Calculer LF
EXERCICE
II :

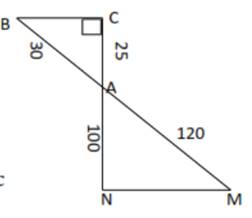
EXERCICE IlI : Soit un triangle RSQ tel
que représenté sur la figure ci-dessous :
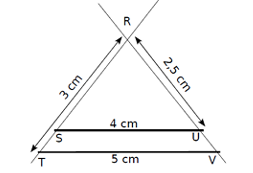
Les droites (SU) et
(TV) étant parallèles,
1.Calculer RS
2. Calculer RV
3. Calculer ST
EXERCICE IV: Soient deux droites (BN)et(CM)
sécantes en un point A. On donne :
MN=0,7 cm, BC=2,1cm, 7MC=2,4 cm
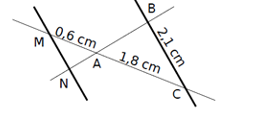
En considérant que les droites (MN) et (BC) étant parallèles, calculer AN
EXERCICE V :
La figure ci-dessous représente le plan de la
charpente d’une maison. AB=20 m, AM=8 m et AC=15m.
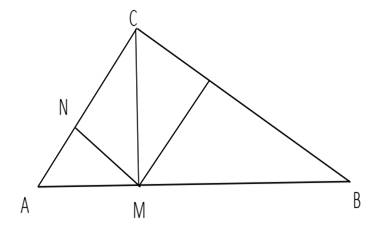
En considérant que les droites (MN) et (BC)
sont parallèles, calculer la distance AN
EXERCICES
VI :
Situation :
Un arbre poussant
verticalement sur le flanc d’une colline a été casse en R par la foudre. Sa
pointe touche le sol a 12 m du pied. Un bâton ST est placé verticalement.
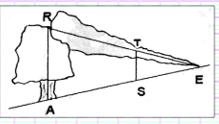
Le propriétaire du terrain
a deux idées :
1ere idée :
-tronçonner la partie
RE de l’arbre et la vendre à 1000 frs par mètre pour le bois de chauffage.
-produire des
planches avec la partie AR. Il estime obtenir des planches de longueur L=AR. Le
tronc AR peut être assimilé à un cylindre de diamètre D=80 cm et Cade hauteur
h=AR. Une planche coute 2500frs la pièce.
2eme idée :
-vendre l’arbre en
entier à 2000frs par mètre a un vendeur de bois.
On
donne :ST=2m ; ES=4m et ET=5m.
Taches :
1.Combien le
propriétaire va-il encaisser dans la vente du bois de chauffage ?
2.Quel sera le
montant des planches d’épaisseur 2,5 cm qu’il peut obtenir ?
3.Quelle idée est
avantageuse pour le propriétaire ?
CORRIGES
EXERCICE I :
1.Les
droites (ST) et (FL) sont parallèles car elles admettent une perpendiculaire
commune qui est la droite (SR).
2. D’après
le théorème de Thales :
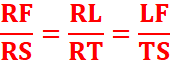
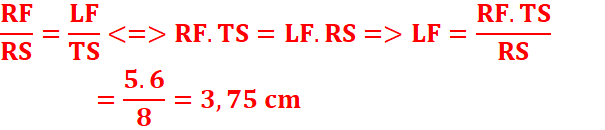
EXERCICE II :
1.a)![]() =
=
![]() =
=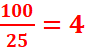
b)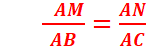
2. (MN)//(BC)
EXERCICE IlI :

Les droites
(SU) et (TV) étant parallèles, d’après le théorème de Thales :
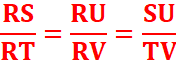
1.
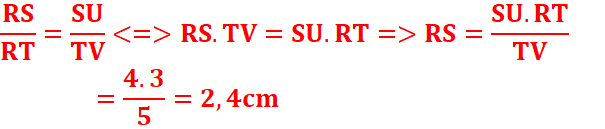
2.
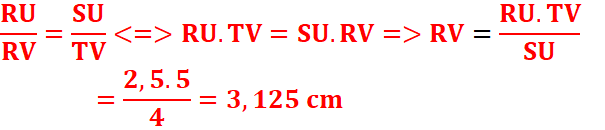
3.
ST=RT-RS=3-2,4=0,6cm
EXERCICE IV:

Les droites
(SU) et (TV) étant parallèles, d’après le théorème de Thales :
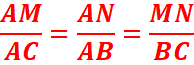
 cm
cm
EXERCICE V :

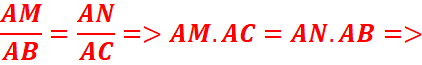

EXERCICES
VI :
Situation :
Un arbre poussant
verticalement sur le flanc d’une colline a été casse en R par la foudre. Sa
pointe touche le sol a 12 m du pied. Un bâton ST est placé verticalement.

Le propriétaire du
terrain a deux idées :
1ere idée :
-tronçonner la partie
RE de l’arbre et la vendre à 1000 frs par mètre pour le bois de chauffage.
-produire des
planches avec la partie AR. Il estime obtenir des planches de longueur L=AR. Le
tronc AR peut être assimilé à un cylindre de diamètre D=80 cm et de hauteur h=AR. Une
planche coute 2500frs la pièce.
2eme idée :
-vendre l’arbre en
entier à 2000frs par mètre a un vendeur de bois.
On
donne :ST=2m ; ES=4m et ET=5m.
Taches :
1.Combien le
propriétaire va-il encaisser dans la vente du bois de chauffage ?
2.Quel sera le
montant des planches d’épaisseur 2,5 cm qu’il peut obtenir ?
3.Quelle idée est
avantageuse pour le propriétaire ?
EXERCICE VI :
1.Combien
le propriétaire va-il encaisser dans la vente du bois de chauffage ?
Les droites
(ST) et (RA) sont parallèles. Donc d’après le théorème de Thales, nous
avons. :
![]()
![]()
Montant :15x1000=15000frs
2.Quel sera
le montant des planches d’épaisseur 2,5 cm peut-il obtenir ?
Soit n le
nombre de planches d’épaisseur e=2.5 cm. on a :
D=2.5n =>
n=D/2.5=80 :2,5=32 planches
Montant :32x2500=80000frs
3.Quelle
proposition est avantageuse pour le propriétaire
![]()
![]()
Hauteur de
l’arbre : AR+RE=6+15=21
Montant :21x2000=42000
frs