MOUVEMENTS RECTILIGNES
(CINEMATIQUE)
PARAMETRES CINEMATIQUES DU
MOUVEMENT
Repère d’espace, repère de
temps
L’état de mouvement ou de repos est relatif. Nous pouvons
par exemple nous déplacer sans marcher sur un escalier roulant ; de même
une personne assise dans un train est immobile par rapport à son compagnon de
voyage mais en mouvement par rapport à un observateur debout sur le quai.
Le référentiel étant choisi,
plusieurs repères d’espaces peuvent lui être associés.
·
Un repère d’espace est l’association d’un
point O nommé origine et d’une base formée de trois vecteurs.
Le repère cartésien noté (![]() ,
,![]() ) est le plus utilisé.
) est le plus utilisé.
·
La
connaissance d’un repère de temps
est également nécessaire. Chaque instant d’observation est appelé date et est
noté t. L’instant d’origine est dans la plupart des cas, l’instant du début de
l’expérience.
Trajectoire
La trajectoire d’un système est
l’ensemble des positions successives qu’il occupe au cours
de son mouvement.
On distingue trois grands types de trajectoire :
— si la trajectoire est une ligne
droite, le mouvement est rectiligne
;
— si la trajectoire est un cercle,
le mouvement est circulaire ;
— si la trajectoire est une courbe,
le mouvement est curviligne.
Exemple :
Le mouvement d’un mobile est défini par :
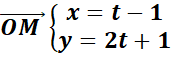
Trouvons l’équation cartésienne de la trajectoire de ce mouvement.
![]()
![]()
=>y=2x+3 qui est
l’équation de la trajectoire. C’est une droite.
Vecteur
position et vecteur déplacement
Vecteur
position
La position d’un mobile M est déterminée à chaque instant par son vecteur
position
Le mouvement d’un mobile se déplaçant dans l’espace peut être décrit dans
un repère cartésien (![]() ,
,![]() )
)
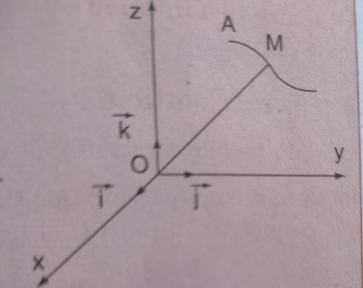
Le vecteur position est alors
![]() =x
=x![]()
x,y et z sont
les coordonnées cartésiennes du point M.
Soit M1, la
position du mobile à la date t1 et M2 la position à la
date t2,
Le vecteur ![]() est appelé vecteur déplacement de ce
mobile au cours de l’intervalle de temps Δt
=t2 – t1
est appelé vecteur déplacement de ce
mobile au cours de l’intervalle de temps Δt
=t2 – t1
![]() -
-![]()
Le vecteur déplacement correspondant à la variation du vecteur position.
Si dans un référentiel, la trajectoire du point M est connue, on peut
repérer le point par la mesure de l’arc ![]() s=mes AM est appelé abscisse curviligne
s=mes AM est appelé abscisse curviligne
Ce vecteur a
pour :
⎯ direction : la
droite (MM’) ;
⎯ sens : celui
du mouvement (de M vers M’) ;
⎯ valeur : la
distance entre M et M’.
Vecteur
déplacement
Lorsqu’un système se déplace entre
deux positions appelées M et M’, on peut définir un vecteur déplacement
Vitesse moyenne
La
vitesse moyenne d’un corps entre deux instants t1 et t2
correspond à la distance parcourue par ce corps, divisée par la durée de
parcours t2-t1.
Le vecteur vitesse moyenne ![]() moy est le
quotient du vecteur déplacement du mobile à l’intervalle de temps
correspondant.
moy est le
quotient du vecteur déplacement du mobile à l’intervalle de temps
correspondant.
Le vecteur vitesse moyenne a pour :
⎯ direction : la droite (MM’)
;
⎯ sens : celui du mouvement
(de M vers M’) ;
⎯ valeur :
Unité : le mètre par seconde(m/s) 1m/s=3,6km/h
Le vecteur vitesse moyenne est indépendant
de la trajectoire du système entre M et M’, et il est colinéaire au vecteur déplacement ![]()
Exemple :
Nous pouvons voir que le vecteur vitesse moyenne est colinéaire à
Distance entre M et M’ : 𝑀𝑀′ = 30 - 5 = 25 m
Durée du parcours : 𝛥𝑡 = 10 - 1 = 9 𝑠
Vitesse moyenne : 𝑣𝑚𝑜𝑦 =
25 :9 ≈ 2,78 𝑚/𝑠
Vecteur vitesse instantanée
Le vecteur vitesse instantanée ![]() est la limite vers laquelle tend le
vecteur vitesse moyenne quand l’intervalle de temps Δt devient très petit.
est la limite vers laquelle tend le
vecteur vitesse moyenne quand l’intervalle de temps Δt devient très petit.
![]() =
=![]() =
= 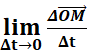 =
= ![]()
Le vecteur
vitesse instantanée d’un mobile à un instant t est la dérivée par rapport au
temps du vecteur position ![]() à cet instant.
à cet instant.
Dans un
repère cartésien, le vecteur vitesse s’écrit :
![]() =
= ![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
La vitesse linéaire instantanée correspond à la dérivée par rapport au temps
d’abscisse curviligne s :
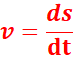
Le vecteur vitesse
instantanée ![]() en un point de la trajectoire du système est une vitesse moyenne calculée
sur un intervalle de temps très court.
en un point de la trajectoire du système est une vitesse moyenne calculée
sur un intervalle de temps très court.
Le sens et la direction sont confondus avec la tangente en ce point.
Le vecteur vitesse instantanée 𝑣 a pour :
⎯ direction : la tangente de
la trajectoire ;
⎯ sens : celui du mouvement ;
⎯ valeur : v=ds/dt
Exemple : Le mouvement
d’un mobile est défini par :
![]()
Calculons la
vitesse de ce mobile :
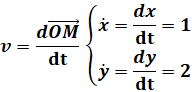
Vecteur
accélération
L’accélération d’un mobile caractérise la variation de sa vitesse.
Le vecteur accélération moyenne entre deux instants t1 et t2
est :![]()
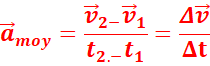
Unité : le mètre
par seconde carré (m/s2)
Le vecteur accélération instantanée est donné par la relation :
![]()
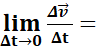
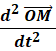
Le vecteur accélération instantanée est donc la dérivée seconde par
rapport au temps du vecteur position.
Dans un repère cartésien (O,![]() ), le vecteur vitesse s’écrit :
), le vecteur vitesse s’écrit :
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]()
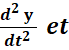
![]()
![]()
Exemple :
Le mouvement d’un mobile est défini par :
![]()
Calculons l’accélération
de ce mobile :
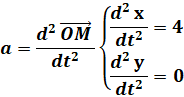
TYPES
DE MOUVEMENTS
Mouvement
rectiligne uniforme
Un mouvement rectiligne uniforme
est un mouvement pour lequel :
-la trajectoire est une droite
- la valeur de la vitesse est constante (v=cte)
donc l’accélération est nulle(a=0).
Equation horaire du mouvement :
x=vt +x0
x (en
mètres) est l’abscisse à l’instant t
(en secondes)
x0(en
mètres) est l’abscisse à l’instant t=0 (en secondes)
v (en mètres
par seconde) est la vitesse
Mouvement rectiligne uniformément varié
Un mouvement
rectiligne uniformément varié est un mouvement pour lequel :
-la trajectoire est une droite
- la vitesse varie de manière uniforme avec le temps (l’accélération est
nulle).
Equations horaires :
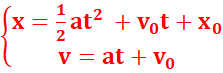
x (en
mètres) est l’abscisse à l’instant t
(en secondes)
x0(en
mètres) est l’abscisse à l’instant t=0 (en secondes)
v (en mètres
par seconde) est la vitesse
Relation indépendante du temps entre
les vitesses et les abscisses :
![]() -
-![]()
Le mouvement est uniformément varié :
- Mouvement
rectiligne uniformément accéléré si le vecteur vitesse augmente.
- Mouvement
rectiligne uniformément décéléré si le vecteur vitesse diminue.
Remarques :
a- Au cours d’un mouvement rectiligne uniforme, la
distance entre les points ne change pas au cours du temps car la vitesse reste
constante. Par ailleurs, la direction de 𝑣 ne change pas.
b-Au cours d’un mouvement rectiligne
accéléré, la distance entre les points augmente au cours du temps car la
vitesse augmente progressivement. En revanche, la direction de 𝑣 ne change
pas.
c-Au cours d’un mouvement rectiligne décéléré, la distance entre les points
diminue au cours du temps car la vitesse diminue progressivement. En revanche,
la direction de 𝑣 ne change pas jusqu’à l’arrêt du système.
EXERCICES.
EXERCICE I :
Les
équations paramétriques d’un mobile sont :
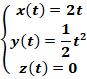
1. Le mouvement du mobile est-il
plan ? Pourquoi ?
2. Déterminer le module des vecteurs
vitesse et accélération à l’instant t=0
3. Quelle est l’équation de sa
trajectoire ?
EXERCICE II
L’équation horaire d’un mobile en
mouvement rectiligne sur un axe x’ox est :
x(t)=3t-1 (m)
1. Déterminer le module du vecteur
vitesse de ce mobile
2.Calculer la vitesse moyenne de ce
mobile entre les instants t1=1s et t2=2s
3.Déduire l’accélération moyenne.
4.calculer V1 et V2
et comparer à Vmoy
EXERCICE III :
1. Un mobile, animé d’un mouvement rectiligne
uniforme, a déjà parcouru 20 m à la date 0 (instant initial). Sa vitesse est de
60 m/s.
a) Ecrire
l’équation horaire de son mouvement.
b) Quelle
distance aura-t-il parcouru après 1h ?
2. Un mobile initialement au repos, parcourt
une distance de 12 km en 20mn à vitesse constante. Calculer cette vitesse.
EXERCICE III:
On donne les équations horaires d’un mouvement
décrit par un mobile M.
x= 5t2 +25t+15 (m)
v=10t+25 (m/s)
1. Quelle est la
nature de ce mouvement ?
2. a)Identifier
l’accélération de ce mouvement ?
b) Identifier la position initiale du mobile
c) Identifier la vitesse initiale du
mobile
3. Un mobile
en mouvement rectiligne uniformément varié maintient une accélération constante
de 10 m/s2. A l’instant initial, le mobile a déjà parcouru 25 m avec
une vitesse initiale de 20m/s.
3.1 Ecrire les
équations horaires du mouvement de ce mobile.
3.2 Calculer sa
vitesse après 100 m de parcours
EXERCICE V :
Une automobile roule à la vitesse de 90km/h, le
conducteur apercevant un obstacle freine. La vitesse diminue de 5m/s pendant
chaque seconde.
1. Exprimer V
en m/s
2. Calculer :
a)La vitesse de l’automobile 2s après le début de
freinage
b) son accélération
EXERCICES VI :
Partant du point A (VA=0), un mobile en
mouvement rectiligne acquiert une vitesse de 10 m/s après 25 m de parcours et
arrive au point B avec une vitesse VB. Il parcourt ensuite 50m avec
cette vitesse jusqu’au point C en mouvement uniforme. Il s’arrête à 125 m de
son point de départ au point D. Le mouvement de cette phase est uniformément
retardé.
1. Définir :
mouvement rectiligne ; trajectoire
2 .Calculer la
durée totale du mouvement du mobile.
3 .Etablir les
équations horaires des mouvements des trois phases
4 .Construire
les diagrammes des espaces, des vitesses et des accélérations
CORRIGES
EXERCICE
I :
1.Oui.
parce que les équations se réduisent à deux coordonnées x(t) et y(t), donc le
mouvement est plan.
2.Vitesse :Vx=2
,Vy =t et ![]()
A
t=0 ,![]()
![]() cm/s
cm/s
Accélération :
ax=0, ay=1 et
![]() =
=![]()
3.![]()
![]()
![]() =
=![]()
![]()
EXERCICE
II
1.
Vitesse :Vx=3 , et
![]() =
=![]()
2.
![]() =
=![]() =3m/s
=3m/s
3.Accélération :
amoy = 0,
4.![]() V1=
V1=![]()
V2 =![]()
=>
V1 < V2 <Vmoy
EXERCICE III:
1. MRUV
2.
2.1
Par identification![]()
![]() =5t2 +25t+15
=5t2 +25t+15
< =>![]()
![]()
![]()
2.2.![]()
![]() =5t2 +25t+15
=5t2 +25t+15
< =>![]()
2.3.![]()
![]() =5t2 +25t+15
=5t2 +25t+15
ó ![]() =25m/s.
=25m/s.
3.
3.1. Les équations du MRUV
sont :
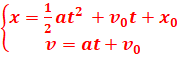
La relation indépendante
entre les vitesses et les abscisses :
![]() -
-![]()
a=10
m.s-1, x0=25m, v0=20ms-1
=>
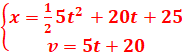
3.2.![]() –
–![]()
![]()
=![]() =43,6m/s
=43,6m/s
EXERCICE IV :
1.
1.1. Vitesse en m/s :![]() =25m/s
=25m/s
1.2.La vitesse varie de 0(répos) à 25m/s donc on à faire à un MUV d’équations
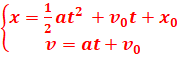
La relation indépendante
entre les vitesses et les abscisses :
![]() -
-![]()
L’instant initial (t=0),
le véhicule est au repos(v0=0), les équations deviennent
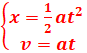 et
et ![]()
![]()
![]()
![]()
![]() =>x=
=>x=![]() =
=![]() =
=![]() =
=![]() =375m
=375m
2.
2.1.La vitesse varie de 0
à 10 m/s donc c’est un MRUV d’équations
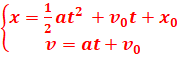
A la date 0,![]() les équations
deviennent
les équations
deviennent
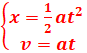 et
et ![]()
![]()
2.2![]() =
=![]() =3,33m/s
=3,33m/s
2.3.
![]()
![]() =
=![]() =15m
=15m
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire