PRIMITIVES
DEFINITION
f est une fonction définie sur un intervalle I. On appelle primitive sur I
de f toute fonction F dérivable sur I tel que f est la dérivée de F.
Propriété
Toute fonction continue sur un intervalle I admet une primitive sur I.
Primitives
d’une même fonction
Si la fonction F est une primitive de la fonction f sur l’intervalle I,
alors pour tout nombre réel c, la fonction x→F(x)
+c , c ϵ IR est une primitive sur I de f.
Toute primitive sur I de f est de cette forme.
Exemple :
x2 a pour primitives ![]()
Primitive
d’une fonction vérifiant une condition initiale
F est une fonction continue sur un intervalle I, x0 est un
nombre réel de I et y0 un nombre réel. Il existe une seule primitive de la fonction f
sur l’intervalle I qui prend la valeur y0 en x0.
Exemple :
Calculons la primitive de la fonction f(x)=x2 qui prend la
valeur ![]() en x0.
en x0.
La primitive de f est F(x)=![]() +k
+k
F(0)=![]() +k donc
+k donc ![]() =0+k =>k=
=0+k =>k=![]() et F(x)=
et F(x)=![]()
DETERMINATION
DES PRIMITIVES
Primitives
des fonctions élémentaires
La connaissance des dérivées des élémentaires permet de dresser le tableau
suivant, où .


Primitives
des fonctions composées
Soient U et V les primitives
respectives des fonctions u et v sur un intervalle I;
k un nombre réel
- La fonction u+v admet pour primitive sur la
fonction U+V;
- La fonction ku admet pour primitive sur la fonction
kU .
-Soit u une fonction dérivable sur un intervalle Iet
v une fonction dérivable sur un intervalle contenant u(I). La fonction u’x(v’ou) admet pour primitive
sur I la fonction (vou).
On en déduit le tableau suivant :
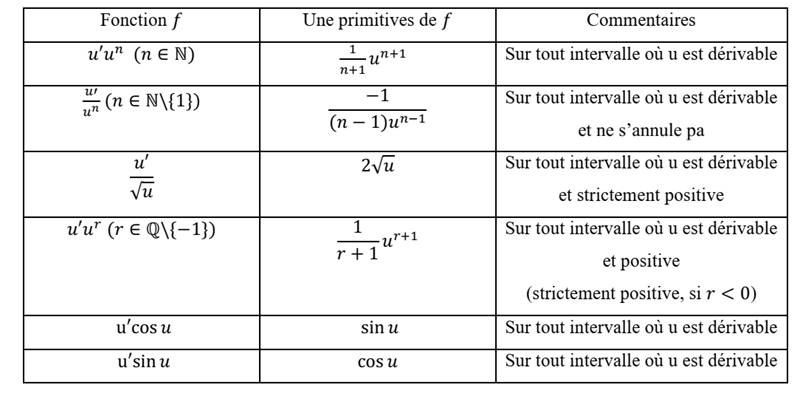
Remarques :
1.

2.Pour déterminer les primitives des fonctions trigonométriques du type x→(sinx)m(cosx)n,
(m,n ϵ IN)
, on peut utiliser l’un des procédés suivants :
- Si n et m sont de même parité, linéariser sinmxcosnx;
- Si n et m sont de parités différentes, utiliser sin2x +cos2x
=1 et écrire sinmxcosnx sous la
forme sinxP(cosx)
si m est impair ou cosxP(sinx)
si n est impair, P désignant un polynôme.
EXERCICES
EXERCICE
I :
Déterminer
les primitives de fonctions suivantes :
a.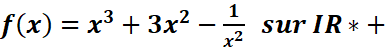
b.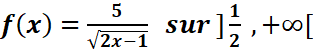
c. IR
IR
d.

e.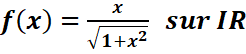
EXERCICE
II :
1. Déterminer les
primitives de fonctions suivantes :
a.![]()
b. ![]()

EXERCICE
III :
Déterminer les primitives de fonctions suivantes :
a.
b. 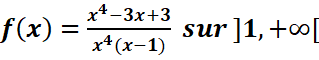
CORRIGES
EXERCICE I :
a. 
b. ![]()
//on pose :u=2x-1


c. 
// on
pose : 
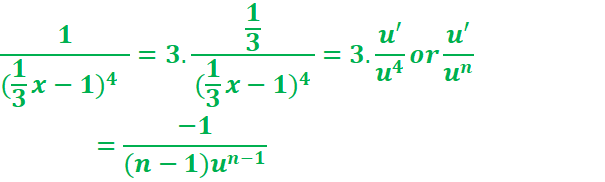
e. ![]()
//on pose :u=1+x2
 =
=

EXERCICE II :
1.
a.
//![]()
![]()
![]()
b. ,
,![]()
// 

2.
a)
·
![]() =
=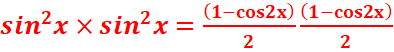
=
·
![]() =
=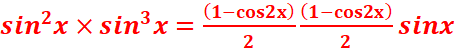
=

= +
+ 
b)
·
 ,
, ![]()
· 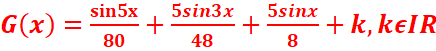
c) 
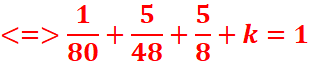
EXERCICE III
a.
Sa primitive est :

b. 
Sa primitive est :

//ln est le logarithme népérien car
primitive de
![]()
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez
un commentaire
