NOMBRES RATIONNELS
INTRODUCTION
Un nombre rationnel est un nombre qui peut
s’exprimer sous la forme d’une fraction, c.-à-d. comme quotient de deux nombres
entiers. Les nombres rationnels incluent les fractions, les nombres entiers et
les décimaux qui peuvent être exprimés sous forme de fraction.
Exemples :3/4, -1/5
Toutes les fractions sont des rationnels,
mais tous les rationnels ne sont pas forcément des fractions. Par exemple, 3
est un rationnel (3/1), mais il n’est pas nécessairement représenté sous forme
de fraction.
Définition :
L’ensemble des nombres qui peuvent
s’écrire sous la forme ![]() , où a est un nombre
entier relatif et b un nombre entier relatif non nul est appelé ensemble
des nombres rationnels. Cet ensemble se note ℚ.
, où a est un nombre
entier relatif et b un nombre entier relatif non nul est appelé ensemble
des nombres rationnels. Cet ensemble se note ℚ.
Remarque :
Si la division de a
par b admet une écriture décimale infinie et périodique, alors est un nombre
rationnel non décimal.
Rappel : Un nombre décimal est un nombre qui peut s’écrire avec une virgule ou non
et avec un nombre limité de chiffres après la virgule.
OPERATIONS
SUR LES NOMBRES RATIONNELS
Inverse
Soit une
fraction ![]() avec b≠0
avec b≠0
L’inverse de
cette fraction est : 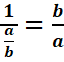
Simplification
Pour simplifier une fraction, on trouve un diviseur
commun a ses deux termes. Ensuite on divise le numérateur et le dénominateur
par ce diviseur commun.
Exemple :
On veut
simplifier la fraction ![]()
On constate
que les deux termes de cette fraction sont divisibles par 3
On a
donc : 
On ne peut
plus trouver un diviseur commun a 4 et 117. On dit que la fraction ![]() est irréductible.
est irréductible.
Rendre une fraction
irréductible
Une fraction irréductible est une fraction
dont le seul diviseur commun au numérateur et au dénominateur est 1. Pour
rendre une fraction irréductible, on peut simplifier cette fraction par le pgcd
du numérateur et du dénominateur.
Exemple : rendre irréductible les fractions
suivantes : ![]()
Pgcd(228,120)=4

NB : On peut aussi faire des simplifications successives.
Réduire deux fractions au
même dénominateur
Pour réduire deux fractions ![]() aux mêmes dénominateurs on multiplie
le numérateur et le dénominateur de la première fraction par le dénominateur de
la deuxième fraction et on multiplie le numérateur et le dénominateur de la
deuxième fraction par le dénominateur de la première fraction
aux mêmes dénominateurs on multiplie
le numérateur et le dénominateur de la première fraction par le dénominateur de
la deuxième fraction et on multiplie le numérateur et le dénominateur de la
deuxième fraction par le dénominateur de la première fraction


Exemple : Mettre ![]() et
et ![]() au meme
denominateur
au meme
denominateur


Addition et soustraction
Soient a, b,
c et d quatre nombres entiers relatifs avec b≠0 et d≠0
·
Les deux fractions ont un même dénominateur


Règle : On additionne(retranche) les
numérateurs et on garde le dénominateur commun
Exemples :


·
Les deux fractions ont des dénominateurs différents
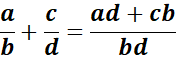

Règle : On réduit les fractions au même dénominateur, on obtient deux fractions avec le même dénominateur et on revient au cas précèdent.
Exemples :

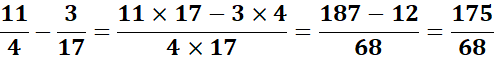
Multiplication
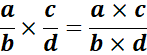
Règle : On multiplie les numérateurs
entre eux et les dénominateurs entre eux.
Exemple :

Division

Règle : On multiplie la fraction
dividende par la fraction diviseur renversée.
Exemple :
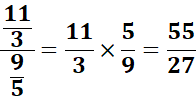
Propriété : Pour tout réels a, b, c et d avec b
et d différents de zéro
![]()
Exemple : Déterminons x pour qu’on ait 

EXERCICES
EXERCICE I :
1- Ecrire sous forme décimale : 
2- Ecrire sous forme fractionnaire :2,5 et 8,55
3- Parmi les nombres rationnels suivants :![]() ;
;![]() ; -
; -![]() ;8
;8
Écrire ceux qui sont des nombres décimaux relatifs.
4-
![]()

5-Rendre irreductible
les fractions 
EXERCICE II :
Effectue les opérations suivantes et donne le résultat sous la forme d’une
fraction irréductible :

EXERCICE III:
Situation :
Un établissement d’enseignement
secondaire a présenté 200 candidats aux différents examens (BEPC, PROBATOIRE et
BAC), session de 2025
dans les proportions suivantes :
-BEPC :3/5 des candidats présentés.
-PROBATOIRE : 1/4 des candidats présentés.
-BAC : le reste des candidats présentés.
On connait par ailleurs le nombre de candidats admis :
-BEPC :60
-PROBATOIRE : 40
-BAC : 18
Taches :
1. Quel est le nombre de candidats présentés pour chaque examen ?
2.Quelle fraction représente les candidats au BAC ?
3.Calculer le taux de réussite global de cet établissement.
EXERCICE IV :
Situation :
Pour recevoir ses amis, Bijou prépare un
cocktail de jus de fruit. Dans un pot gradue, elle met les 3/8 de jus d’orange
et les 0,15 de jus de papaye. Elle rajoute ensuite le jus d’ananas pour qu’il y
ait trois fois plus de jus de papaye, puis elle complète le pot avec le sirop
de grenadine.
1. Calculer la proportion du jus d’ananas.
2. Déterminer l’ecriture en ligne de la proportion du sirop de grenadine.
3.Calculer la proportion du sirop de grenadine.
EXERCICE V :
Situation :
Anna entre dans un supermarché avec
19200 FCFA pour faire des achats. Elle utilise le quart de cette somme pour
acheter des ustensiles de cuisine, le tiers du reste pour acheter les produits
de beauté qu’elle pourra revendre. Elle règle également une dette dont le
montant correspond à 12,5% du montant encore disponible.
1-Quel est le montant des ustensiles
de cuisine ?
2- Quel est le montant des produits
de beauté ?
3- Y a-t-il un reste après ces
dépenses ?
EXERCICE VI:
Dans une classe
de 3e, 2 /3 des élèves désirent poursuivre leurs études en seconde
d’enseignement général,
1/ 6 veulent
aller en seconde technique et les 5 élèves restant souhaitent aller en seconde littéraire.
1. Quelle
fraction du nombre d’élèves de la classe veut aller en seconde littéraire ?
2.
Déterminer le nombre d’élèves de la classe.
3.
Déterminer le nombre d’élèves de la classe désirant poursuivre leurs études en
seconde d’enseignement général.
CORRIGES
EXERCICE I :
1- Ecrivons sous forme décimale :


2- Ecrivons sous forme fractionnaire


3- Parmi les
nombres rationnels suivants :![]() ;
;![]() ; -
; -![]() .
.
Les nombres décimaux relatifs sont : 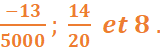
4-
![]()
![]()
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]()
![]()
5-Rendons irreductibles les fractions 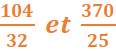
pgcd(104,32)=8
=>
// on peut
aussi faire des simplifications successives :

pgcd(370,25)=5
=>
EXERCICE II :
A=![]() =
=![]() =
=![]() =
=![]()
B=![]() =
=![]() =
=![]() =-
=-![]()
C=![]() =
=![]() =
=![]() = -
= -![]()
E=![]()
![]()
![]()
![]() )
) ![]()
![]() =
=![]() =
=![]() =
=![]()
F=(![]() )
)![]()
![]() =(
=(![]() )
)![]()
![]() =
=![]()
![]()
![]() =
=![]() =
=![]() =
=![]()
G=![]() x (
x (![]() )=
)=![]() =
=![]()
X=![]() =
=![]()
Y=![]() =9x
=9x![]() =
=![]() =24
=24
Z=![]() =
=![]() x
x![]() =
=![]()
P=(![]() )x
)x ![]() =
=![]() =
=![]() =
=![]()
Q=![]() x(
x(![]() )=
)=![]() x(
x(![]() )=
)=![]()
EXERCICE III :
1.BEPC :3/5 x200=120 candidats
PROBATOIRE :1/4 x200=50
BAC :200-(120 +50)=30
2. 30 represente
les 3/20 de 200 car 3/20 x200=30
3. Nombre de candidats admis :60+40+18=118
Taux de réussite :118/200 x 100=59%
EXERCICE IV :

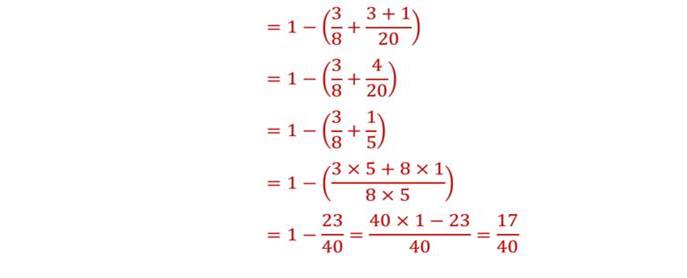
EXERCICE V.
1-Achat des ustensiles
de cuisine :1/4 x19200=4800
FCFA
2-Achat des produits
de beauté : tiers du reste 1/3(19200-4800)=4800
FCFA
3. Montant encore
disponible :19200-(4800+4800)=9600 FCFA
Dette :1 2,5% x 9600=1200 FCFA
Reste : 19200-(4800+4800+1200) =8400
FCFA