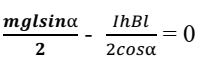FORCES MAGNETIQUES

CHAMP MAGNÉTIQUE

Définition

Le champ magnétique est une propriété de toute région de l’espace à l’intérieur de laquelle un objet ferromagnétique est soumis à des forces magnétiques. On caractérise le champ magnétique en tout point M par le vecteur induction magnétique

-de point d’application M

-de direction correspondant à celle prise par une aiguille aimantée placée en M.

- de sens dirigé du pôle sud au pôle nord de l’aiguille aimanté.

- d’intensité donnée par un tesla mètre ou une sonde de Hall en tesla.

Spectre magnétique

Une ligne de champ est une courbe tangente, en chacun de ses points, au vecteur champ
magnétique et orientée dans le même sens que .

• Un spectre magnétique est un ensemble de lignes de champ.

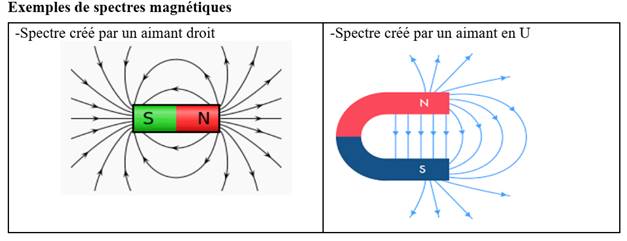
Champ uniforme

Un champ magnétique est uniforme si le vecteur induction conserve la même direction et la même grandeur.

Les lignes de champ sont parallèles dans un champ uniforme (intérieur d’un aimant en U, intérieur d’un solénoïde, etc..)

FORCE DE LAPLACE

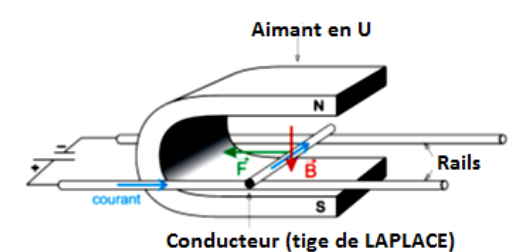
Mise en évidence de la force de Laplace

Un conducteur peut rouler sur deux rails parallèles et horizontaux. Les extrémités de ces rails sont reliées à un générateur. Un ampèremètre contrôle le passage du courant. Le conducteur est placé dans l’entrefer d’un aimant en U qui établit un champ magnétique vertical. La force de Laplace est mise en évidence par le déplacement du conducteur (tige de Laplace).

Enoncé de la loi de Laplace

Une portion rectiligne de conducteur de longueur parcouru par un courant d’intensité i et placé dans un champ magnétique, est soumise à une force électromagnétique dite de Laplace appliquée au milieu de la portion et donnée par la relation :

Caractéristiques :
-point d’application : le milieu du conducteur.
-Direction : orthogonale au plan formé par les vecteurs iet  , le vecteur iétant orienté dans le sens du courant.
-sens : est donné par la règle des trois doigts de la main droite.
-son intensité est : F=ilBsinɑ

Règle des trois doigts de la main droite :

Le pouce étant placé le long de l’élément MN dans le sens du courant et l’index indiquant la direction et le sens du vecteur induction , le majeur, tendu perpendiculairement aux deux autres doigts, indique le sens de la force électromagnétique.

FORCE DE LORENTZ

L’action d’un champ magnétique sur une particule chargée en mouvement montre l’existence d’une force magnétique agissant sur la particule.

On appelle cette force la force de Lorentz. On peut la mettre sous la forme

Caractéristiques :

-direction : perpendiculaire à la fois au vecteur vitesse et au vecteur champ magnétique

-sens : est donné par la règle des trois doigts de la main droite.

-intensité : F=qvbsinɑ

EXERCICES

EXERCICE I :
Un conducteur rectiligne de 0,4 m de longueur et parcouru par un courant constant d’intensité 12 A est placé dans un espace où règne un champ magnétique uniforme d’intensité 0,25 T. On constate que le conducteur se déplace.

1. Identifier la force qui fait déplacer le conducteur.

2. Calculer l’intensité de cette force.

a) Lorsque le conducteur est perpendiculaire au vecteur champ magnétique.

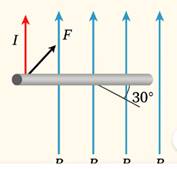
b) Déterminer la valeur de la force magnétique qui s’exerce sur le conducteur quand il fait avec les lignes de champ un angle de 30°.

EXERCICE II :

Les électrons pénètrent dans un champ magnétique perpendiculaire avec une vitesse.

1. Identifier la force qui agit sur cet électron.

2. Calculer l’intensité de la force de Lorentz lorsque v=2.10⁵ m.s^-1 et B=200 mT.

3. Comparer intensité de cette force au poids de l’électron sur terre.

EXERCICE III :

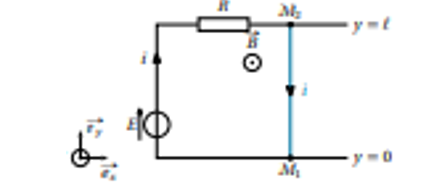
On considère une barre M₁M _; qui glisse sans frottement sur des rails de Laplace . Le circuit est orienté dans le sens indiqué pour l’intensité i sur la figure ci-dessous. On suppose que la résistance totale du circuit fermé vaut R.

(a) Exprimer l’intensité i en fonction de E et R.

(b) Exprimer la force de Laplace qui s’exerce sur la barre en fonction de E, R et B.

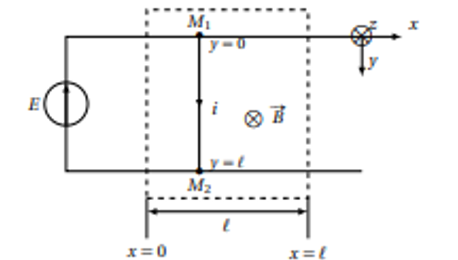
2. On considère la configuration ci-dessous, dans laquelle le champ magnétique est nul sauf dans la zone délimitée par les traits interrompus, de largeur ` égale à la longueur de la barre, où il est uniforme de norme B0. On note de nouveau R la résistance totale du circuit. La barre, de masse m, est lancée de la gauche vers la droite et arrive avec une vitesse v₌ dans la zone de champ magnétique.

Déterminer le temps qu’elle met pour en sortir. On néglige tout frottement mécanique Les deux tiges des rails de la figure ci-dessous sont écartées de 20 cm et la barre cylindrique MN leur est perpendiculaire. Le tout est dans un champ uniforme dont l’induction est normal au plan des rails et a pour intensité B=0,5 T. Les extrémités Q et S sont reliées aux bornes d’un générateur de de fem E=6V et la résistance totale du circuit ainsi réalisé est R=2 Ώ. La vitesse initiale étant v₀=0,3m/s.

EXERCICE IV :

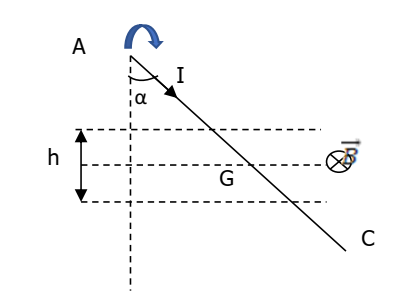
Un conducteur de longueur l et de masse m, est susceptible de tourner autour d’un axe passant par le point A. Dans sa position d’équilibre, le conducteur fait un angle α avec la verticale. Il est alors parcouru par un courant constant d’intensité I. La portion du conducteur soumise au champ magnétique est symétrique par rapport à son centre d’inertie G.
Données : m = 20 g ; g = 10 N/kg ; h = 5 cm ; B = 0,5 T. a = 10°

1. Exprime l’intensité de la force de Laplace qui agit sur le conducteur en fonction de α, I, h et B.
2. Représente sur le schéma, les forces agissant sur le conducteur.
3. Ecris la relation entre les moments de ces forces traduisant l’équilibre du conducteur.
4. Déduis-en l’expression de l’intensité I du courant en fonction de m, g, α, h et B.

5. Calcule I.

EXERCICE V:

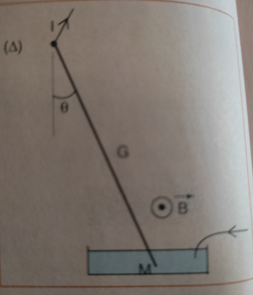
Un fil rectiligne homogène, de longueur OM= 30 cm et de masse 10g, est suspendu par son extrémité supérieure à une point O autour duquel il tourne librement. Son autre extrémité plonge dans du mercure. Ce fil, parcouru par un courant d’intensité 5A, est placé dans un champ magnétique horizontal uniforme. Il s’écarte de la verticale d’un angle Ѳ=11,2° . Le champ agit sur une longueur de 4cm entre deux points situés à 20 cm et 24 cm de O.

1- Faire l’inventaire des forces appliquées à la tige.

2- Appliquer la deuxième condition d’équilibre et déduire la valeur du champ magnétique.

3- Reprendre les calculs pour un champ magnétique formant un angle de 30° au-dessus de l’horizontale.

.

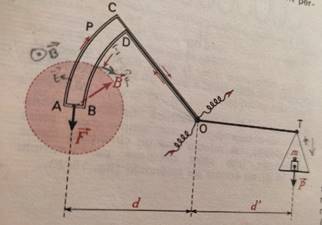
EXERCICE VI :

Une balance de Cotton est constituée par un fléau coudé TOC mobile autour de l’axe horizontal passant par O et portant d’un une palette P en matière isolante limitée par deux arcs de cercle, AC et BD, de centre O, et une partie rectiligne AB située sur le prolongement de TO. Un ruban conducteur où l’on peut faire circuler un courant est appliquée sur le contour de la palette P. L’ensemble est construit de façon que, le plateau étant vide de toute masse marquée, le bras OT soit horizontal quand le fléau est en équilibre en l’absence de courant dans le ruban conducteur. On se sert de cette balance pour mesurer l’induction magnétique du champ pratiquement uniforme qui existe dans l’entrefer d’un électroaimant. A cette fin, la partie inférieure de la palette P est placée dans le champ de façon que le vecteur soit perpendiculaire à son plan.

1.Exprimer l’intensité B de l’induction magnétique en fonction de l’intensité I du courant, de la longueur AB, des distances d et d’, et du poids P des masses marquées m qu’il faut placer dans le plateau pour rétablir l’équilibre.

AN :l=10A,l=2cm,d=d’,m=2g. (g=9,8N/kg)

2.
Une balance de Cotton possède un conducteur actif de 3 cm traversé par un courant de 8A et placé perpendiculairement au vecteur-champ B dont on veut mesurer la valeur. Déterminer la masse m du corps à placer dans le plateau pour équilibrer la balance lorsque B= 0,5T ;

EXERCICE VII :

Le schéma ci-contre représente les bobines de Helmholtz. Le diamètre d’une bobine est D = 10 cm. Chaque bobine possède N = 200 spires.

L’intensité du courant qui circulaire dans chaque bobine est I = 2A.

1.Donner l’intensité du champ magnétique au centre de chaque bobine.

2.Reproduire le schéma et ajouter quelques lignes de champ magnétique entre les bobines.

Préciser le pôle nord et le pôle sud de l’ensemble des deux bobines.

3.Comment peut-on reconnaitre les pôles de la bobine.

EXERCICE VIII : 

Les élèves de terminale D de votre collège ont besoin d’un générateur produisant un courant inférieur à 2 A et une tension inférieure à 350 V pour alimenter un moteur. Ils découvrent au laboratoire un vieux générateur de courant continu ayant perdu sa plaque signalétique. Ne disposant ni de voltmètre et ni d’ampèremètre ils ne savent pas s’ils peuvent l’utiliser. Ils décident alors d’effectuer des expériences pour s’en assurer à partir du matériel disponible au laboratoire.

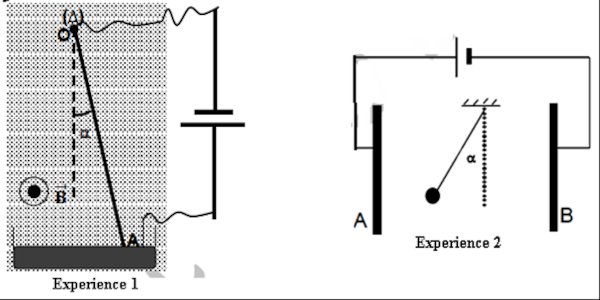
1ère Expérience :
Ils réalisent le montage ci-contre à l’aide de ce générateur. Une tige conductrice OA, homogène, de masse m et de longueur L, est mobile en rotation autour d’un axe horizontal (Δ), passant par son extrémité O. L'autre extrémité A de la tige plonge légèrement dans une cuve à mercure. L'ensemble est plongé dans un champ magnétique →B orthogonal au plan de la figure et de sens sortant produit par un aimant en U.
Lorsque le générateur est connecté, la tige s'écarte de la verticale d'un angle α et s’y maintient en équilibre. On négligera les frottements et on négligera la longueur de la tige qui plonge dans le mercure :
On donne L = 30 cm, α=10o, B = 20 Mt, m = 4,4 g et g = 10 N/kg
2ème Expérience :
Ils réalisent le montage ci-contre à l’aide de ce générateur. Entre deux plaques d’aluminium A et B parallèles est disposé un pendule électrostatique constitué d’une boule électrisée de charge q et de masse m. les plaques sont séparées par une distance d et le pendule a une longueur L. lorsqu’on relie les plaques aux bornes d’un générateur, le pendule s’incline d’un angle α, et s’y maintient en équilibre.
Données : m = 1g, d = 10 cm, g = 10m/s, α=10o et q=5,9×10−7C

Tâche : Sur la base des informations disponibles, ces élèves peuvent-ils utiliser ce générateur pour alimenter le moteur ?

Extrait de l’Épreuve zéro de physique Théorique au baccalauréat D 2025 Région du Nord-Ouest

EXERCICES

EXERCICE I :

1. Identification de la force

La force qui fait déplacer le conducteur est la force de Laplace, notée F.

Elle s’exerce sur un conducteur parcouru par un courant dans un champ magnétique.

2. Formule de la force de Laplace :

F = B × I × L × sin(θ)

- B = intensité du champ magnétique (en T)

- I = intensité du courant (en A)

- L = longueur du conducteur (en m)

- θ = angle entre le conducteur et les lignes du champ B

a) Cas où le conducteur est perpendiculaire au champ

(θ = 90°, donc sin(θ) = 1)

F = 0,25 × 12 × 0,4 × sin(90°)

F = 0,25 × 12 × 0,4 = 1,2 N

→ La force magnétique est 1,2 N.

b) Cas où l’angle est de 30°

sin(30°) = 0,5

F = 0,25 × 12 × 0,4 × 0,5 = 0,6 N

→ La force magnétique est 0,6 N

EXERCICE II :

1. Force qui agit sur l’électron :

C’est la force de Lorentz qui agit sur une charge en mouvement dans un champ magnétique.

2. Intensité de la force de Lorentz :

La formule est : F = |q|·v·B·sin(θ)

Ici, θ = 90° (perpendiculaire) donc sin(θ) = 1

- q = 1,6 × 10⁻¹⁹ C (charge de l’électron)

- v = 2 × 10⁵ m/s

- B = 200 mT = 0,200 T

F = 1,6 × 10⁻¹⁹ × 2 × 10⁵ × 0,2 = 6,4 × 10⁻¹⁵ N

3. Poids de l’électron :

P = m·g

- m = 9,1 × 10⁻³¹ kg

- g = 9,81 m/s²

P = 9,1 × 10⁻³¹ × 9,81 ≈ 8,93 × 10⁻³⁰ N

Comparaison :

F_Lorentz / P ≈ (6,4 × 10⁻¹⁵) / (8,93 × 10⁻³⁰) ≈ 7,17 × 10¹⁴

Conclusion :

La force magnétique est environ 715 000 milliards de fois plus grande que le poids de l’électron. Elle est donc largement dominante

EXERCICE III :

(a) On a immédiatement : i = E/R.

(b) La force de Laplace est alors :

2. On choisit le repère de la figure ci-dessous pour que la force soit selon + pour E ≥ 0. L’intensité, ainsi que l’ensemble du circuit est orientée dans le sens de la flèche représentée sur la même figure.

La force de Laplace est ici immédiatement

On détermine l’intensité en écrivant la loi d’Ohm dans le circuit fermé E = Ri. On a donc finalement :

La dynamique de la barre est régie par la deuxième loi de Newton. Compte tenu de l’hypothèse de glissement sans frottement, la seule force pertinente pour le mouvement selon x est la force de Laplace. Avec le signe de la tension imposée, la tige est accélérée vers la droite. On a, tant que la barre est dans la zone de champ magnétique :

m a = E`B /R =>a=EB/mR.=cte

v=at+v₀ et x=1/2 at²+v₀t +x₀ Avec x₀=0

(1) La date de sortie de la zone de champ magnétique correspond à x =l `.

On résout l’équation du second degré en t suivante :

l=1/2 EB/mR t²+v₀t <=>t²+2Rv0/ElB t -2R/EB=0 soit t²+2x2x0,3/6x0,2x0,5 t -2x2/6x0,5=0 .

t²+2 t -4/3=0 =>t=0,53s

.

EXERCICE IV :

1. F=IlB avec h=lcosα d’où l= ℎ𝑐𝑜𝑠α

et F= 𝐼ℎ𝐵𝑐𝑜𝑠α
2. Les forces réagissant sur la tige
• Force de Laplace 𝐹
• Poids du conducteur 𝑃⃗
• Réaction du support 𝑅⃗
3. A l’équilibre de la balance : ΣM (𝐹ext.)=0
M(𝑹 ⃗)=0 car 𝑹 ⃗⃗ rencontre l’axe de rotation
M (𝑷 ⃗)= 𝒎𝒈𝒍𝒔𝒊𝒏α/2

M (𝑭 ⃗ ) = - 𝐼ℎ𝐵𝑙/2𝑐𝑜𝑠α

ΣM (Fext.)=0

soit

4.

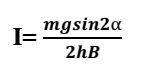
A.N. I=1,36 A

EXERCICE V:

1.

2. . + =

<=>Fd=P.OGsinθ

<=>BIl d= P.OG.sinθ

=>=.

3.C’est la composante horizontale Bcosɑ qui agit.

B’= =

.

EXERCICES VI : BALANCE DE COTTON

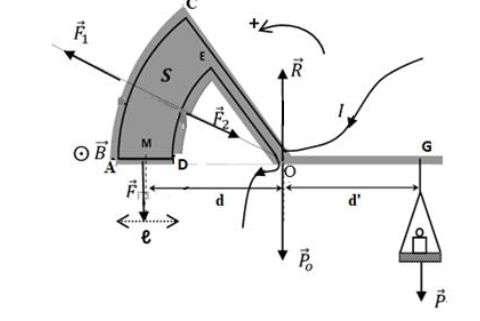
1 • Système : ensemble (fléau + plateau + masse)
• Référentiel terrestre supposé galiléen
• Bilan des forces extérieures au système :
- La réaction 𝑅⃗ ,
- les poids 𝑃⃗ , 𝑃⃗₀,
- les forces de Laplace 𝐹, 𝐹₁ et⃗⃗𝐹⃗ ₂
• À l’équilibre, on a ∑ 𝑀(∆)(𝐹𝑒𝑥𝑡) = 0
𝑀(∆)(𝑃⃗ ) + 𝑀(∆)(𝑅⃗ ) + 𝑀(∆)(𝑃⃗0) + 𝑀(∆)(𝐹) + 𝑀(∆)(𝐹1) + 𝑀(∆)(𝐹2) = 0
Compte tenu de la forme des conducteurs AC et DE (arcs de cercle de centre O), les moments des forces
𝑅⃗ , 𝐹1 ,𝐹2et 𝑃⃗0sont nuls car leurs droites d’action coupe l’axe de rotation (∆) en O.
𝑀(∆)(𝑃⃗ ) + 𝑀(∆)(𝐹) = 0
-𝑃 × 𝑑′ + 𝐹 × 𝑑 = 0 ⟺ 𝐹 × 𝑑 = 𝑃 × 𝑑′
Or 𝐹 = 𝐼ℓ𝐵 et 𝑃 = 𝑚𝑔
𝐼ℓ𝐵 = 𝑚𝑔

⟹
2:
Dans la balance de Cotton, l'expression de la masse est donnée par la relation :
m =𝐼𝑙𝐵/𝑔
A.N. m=8x0,03x0,5/9,8=0.012 kg

EXERCICE VIII : 

Déterminons l’intensité du courant et la tension électrique délivrée par ce générateur puis comparons ces valeurs aux limites du courant et de la tension.
Déterminons l’intensité I du courant à partir de la première expérience en appliquant la condition d’équilibre à la barre.

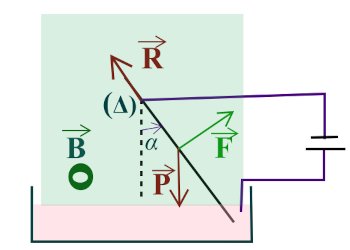
D’après la condition d’équilibre

B×I×L2+0−mgL2sinα =0⇒I=mgsinαBL
AN : I=1,27A
Déterminons la tension électrique U à partir de la deuxième expérience en appliquant la condition d’équilibre à la boule.

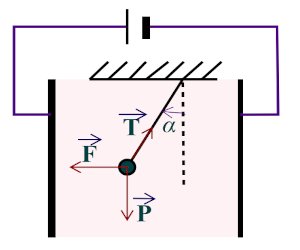
tanα=FP=|q|Ud⇒ U=mg×d|q|tanα
AN : U=298,86V
{I≺2A|U|≺350V, Alors , il peut utiliser ce générateur.

.

Avez-vous un exercice à proposer ?Cliquez-ici

Merci de votre visite
Laissez un commentaire