POUSSEE D’ARCHIMEDE
Expérience
Mesurons le poids
P d’un corps à l’aide d’un dynamomètre, puis plongeons ce corps dans de l’eau
(ou dans un autre liquide) :
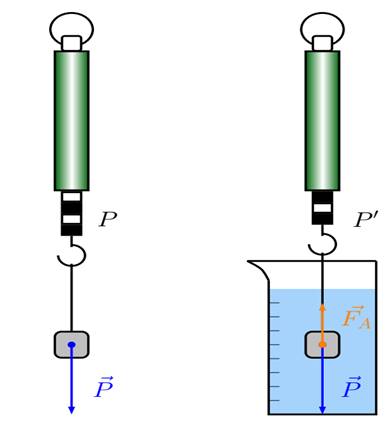
Poids et poids apparent
On constate que le poids du corps plongé dans le liquide semble être
devenu plus petit. Cependant, il est évident que le poids 
n’a pas changé. Il doit donc y avoir une force supplémentaire,
exercée par le liquide sur le corps. Cette force doit être verticale et
orientée vers le haut (elle s’oppose au poids). Cette force s’appelle poussée
d’Archimède. Elle est représentée par le vecteur 
.
La force mesurée par le dynamomètre lorsque le corps plonge dans le liquide est
le poids apparent 
. C’est la force résultante du poids et de la poussée d’Archimède
. Il en résulte que l’intensité de la poussée d’Archimède vaut :
FA = P – P’
On constate de plus que la poussée d’Archimède est indépendante de la
profondeur d’immersion et de l’orientation du corps dans le liquide.
Théorème d'Archimède
« Tout corps plongé dans un fluide au repos, entièrement mouillé
par celui-ci ou traversant sa surface libre subit une force verticale, dirigée
de bas en haut et opposée au poids du volume de fluide déplacé ; cette force
est appelée poussée d'Archimède. »
Pour que le théorème
s'applique il faut que le fluide immergeant et le corps immergé soient au
repos.
Une fois les conditions précédentes respectées, dans un champ de pesanteur
uniforme, la poussée d'Archimède FA est
donnée par la formule suivante :
FA=ρgV
,
ρ est la masse volumique du fluide contenu dans le volume V déplacé,
et g la valeur du champ de pesanteur.
La poussée d'Archimède FA s’exprimera en newton (N) si la
masse volumique ρ est en kg/m3, le volume de fluide
déplacé V en m3 et la valeur de la pesanteur g en N/kg
(ou m/s2).
Corps flottants
Un corps solide
immergé dans un liquide en équilibre est soumis à deux forces verticales et de
sens contraires : son poids et la poussée d’Archimède 
.
Remarque : On suppose que le corps solide est homogène. Dans ce cas, son
centre de gravité et son centre de poussée se confondent.
Trois cas peuvent se présenter :
1. Le poids est plus grand que la poussée d’Archimède. Le corps va aller
vers le bas.
Si la masse volumique d’un corps est plus grande que la masse volumique du
liquide
dans lequel le corps est plongé, le corps va descendre vers le bas (il va
couler).
2. Le poids est plus petit que la
poussée d’Archimède. Le corps va aller vers le haut.
Si la masse volumique d’un corps est plus petite que la masse volumique du
liquide dans lequel le corps est plongé, le corps va monter à la surface du
liquide (il va nager).
3. Le poids est égal à la poussée
d’Archimède. Le corps va rester entre deux eaux.
Si la masse volumique d’un corps est égale à la masse volumique du liquide dans
lequel le corps est plongé, le corps va
flotter, c’est-à-dire il ne va ni descendre, ni monter.
EXERCICES
EXERCICE I:
Une boule cylindrique homogène, non soluble
dans l’eau est suspendue à un dynamomètre. Celui-ci indique 20N lorsque
l’ensemble est dans l’air. Lorsqu’on immerge complètement la boule dans l’eau,
le dynamomètre indique 14N.
1-Donner les caractéristiques du poids de la
boule
2- On admet que la poussée d’Archimède que
subit la boule s’applique au même point que son poids. Quelles sont les autres
caractéristiques de cette poussée ?
3-Representer sur un même schéma le poids de la
boule ainsi que la poussée d’Archimède qu’elle subit de la part de l’eau.
Echelle : 1cm pour 4N
EXERCICE II:
Une noix complètement immergée dans l’eau
déplace un volume d’eau de masse égale à 0,97 kg.
1.
Calcule l’intensité du poids de l’eau déplacée (g=10 N/kg)
2.
Déduis-en la poussée d’Archimède.
3.
L’intensité du poids de la noix est 5 N, la noix coule-t-elle ?
Ou
flotte-t-elle ? Pourquoi ?
EXERCICE III :
Un
vase contient de l’eau. On y immerge un objet solide indéformable. Le niveau
d’eau passe de V1=50cm3 à V2=80cm3.
1.
Calcule le volume V0 de l’objet immergé.
2.
Calcule l’intensité de la poussée d’Archimède.
3.
Calcule la masse de ce solide.
On
donne : 
0=1000kg/m3,
masse volumique de l’eau
s=800kg/m3,
masse volumique du solide
g=10N/kg, intensité de
la pesanteur
CORRIGES
EXERCICE I:
1. Le poids de la boule a
les caractéristiques suivantes :
-point
d’application : Centre de gravité G
-direction :
Verticale.
-sens : Du haut vers
le bas
- intensité : P=
mg=20N (dans l’air)
2. Direction :
verticale
Sens : du bas vers le
haut
Intensité : PA=P-P’=20-14=6N
3.
EXERCICE II:
1. P
=mg=0,97x10=9,7N
2. La poussée
d’Archimède est égale au poids de l’eau déplacée : PA= 9,7N
3. PA>P
donc le corps flotte.
EXERCICE III :
1.V0=V2-V1=80-50=30cm3
2.La poussée
d’Archimède est égale au poids de l’eau déplacée : PA= ρ0V0g=1000x30.10-6x10=0,3N
3. Ms= ρsVs= ρsV0=800x30.10-3=24kg