ÉQUATIONS DE SECOND DEGRE
Définitions :
·
On appelle polynôme ou trinôme du second degré tout
polynôme p de la forme p(x)
= ax2 +
bx +
c, avec a, b et c ![]() IR, a
IR, a![]()
Exemple : p(x)
= 3x2
+ 5x +
c
·
On appelle équation
du second degré, toute équation de la forme ax2 +
bx +
c = 0 avec a, b et c
ε IR, a![]()
Résoudre une équation du
second degré dans IR revient à déterminer les valeurs pouvant être
prises par l’inconnue x et de les regrouper dans un ensemble appelé ensemble
solution et généralement noté S.
Propriété
. La forme canonique du trinôme du second degré p(x)
= ax2+bx+c
est donnée par :
p(x)= ![]()
avec ∆ = b2 - 4ac.
On
appelle discriminant du polynôme p, le réel ∆ défini par Δ=b2-4ac
De cette forme canonique, on a :
1. Si ∆ < 0, alors l’équation p(x) = 0 n’admet pas de
solution dans IR.
2. Si ∆ = 0, alors l’équation p(x)
= 0 admet
une solution double qui est
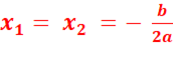
3. Si ∆ > 0, alors l’équation p(x) = 0 admet deux solutions
distinctes qui sont
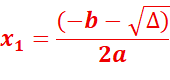
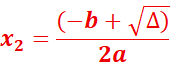
La forme
factorisée du polynôme associé à l’équation (E)
est :
p(x)=a(x-x1)(x-x2)
Exemple : Donner la forme canonique de p(x) = x2 + 6x - 216 puis donne sa forme factorisée
Solution : La forme canonique du
polynôme p(x) est :
![]()
Par identification,
a=1, b=6
c=-216
∆ = 62
- 4(1)(-216)=900
p(x)= [(x+6/2)2
-900/4]
= (x + 3)2 – 225
Pour trouver la forme factorisée, on peut
utiliser l’identité remarquable
a2-b2=(a-b)(a+b) .
(x + 3)2 – 225 =[(x+3)-15][(x+3)+15] ![]()
=(x-12)(x+18)
Forme factorisée : p(x)
= (x + 18)(x - 12)
METHODE :
Pour résoudre une équation du
second degré dans R (E) :
ax2 + bx + c = 0 en utilisant le
discriminant, on calcule
le discriminant :
∆ = b2 -
4ac et on a :
1. Si ∆ < 0, alors l’équation (E) n’admet pas de
solution réelle, son ensemble solution est vide:
S={ }
Le polynôme associé à l’équation (E)
n’est pas factorisable.
2. Si ∆ = 0, alors l’équation (E) admet une solution réelle
double :
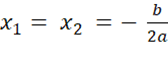
son ensemble solution est S= {- b/2a
}
et la forme
factorisée du polynôme associé à l’équation (E) est :
3. Si ∆ > 0, alors
l’équation (E) admet deux solutions réelles distinctes :
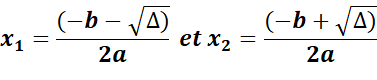
Son ensemble solution est :
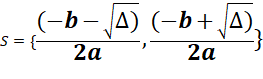
et la forme
factorisée du polynôme associé à l’équation (E) est :
p(x)=a(x-x1)(x-x2)
Exemple :
Résoudre
dans IR : x2+2x-3=0
Solution :
∆=(2)2-4(1)(-3)=4+12=16
x1= (-2-Ѵ16)/2= -3
x2= (-2+Ѵ16)/2= 1
S= {-3,1}
Remarque :
Lorsque le coefficient b
est pair ou contient en évidence le
facteur 2, on
peut poser : b’=b/2.
et calculer le
discriminant réduit Δ’=b’2-ac du polynôme ax2 +
bx +
c.
Trois
cas de figures se présentent :
1. Si Δ’< 0, alors l’équation (E)
n’admet
pas de solution réelle, son ensemble solution est vide et le polynôme associé à
l’équation (E)
n’est
pas factorisable.
2. Si Δ’= 0, alors l’équation (E) admet une solution réelle double, son ensemble solution
est :S=-b’/2
et la forme factorisée du polynôme associé à l’équation (E) est :
![]() )2
)2
3. Si Δ’> 0, alors l’équation (E)
admet
deux solutions réelles distinctes:
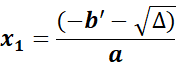
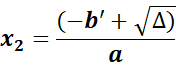
Somme et produit des racines du
trinôme du second degré.
1.Lorsque l’équation du second degré ax2+bx+c = 0 a des
solutions distinctes ou confondues
x1 et x2, leur somme :
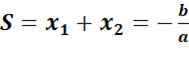
et leur produit ;
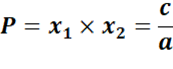
2. Si deux nombres x1 et x2 ont pour
somme S et pour produit P ces nombres sont des solutions
de l’équation :
X2 - SX +
P = 0
à condition que S2 - 4P ≥ 0.
Remarque : Une équation du second
degré possède :
1. Deux solutions de signes contraires lorsque P < 0,
2. Deux solutions positives lorsque ∆ > 0, S > 0 et P
> 0,
3. Deux solutions négatives lorsque ∆ > 0, S < 0 et P
> 0
Exemple: Résoudre
dans IR :
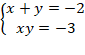
Solution : Il s’agit de résoudre :x2+2x-3=0
avec S=-2 et P=-3
∆=(2)2-4(1)(-3)=4+12=16
x1= (-2-Ѵ16)/2=-3
x2= 1(-2+Ѵ16)/2=1
S={-3,1}
Equations paramétriques
Pour résoudre l’équation de la
forme ax2 + bx + c
= 0 (où c dépend d’un paramètre réel m), On calcule le
discriminant ∆m et la résolution d’une telle équation passe par
l’étude du signe du discriminant ∆m.
Exemple :
Soit m un paramètre
réel. Résoudre et discuter suivant les valeurs de m l’équation (Em) :
-x2 + 4x + 1 - m
= 0
Solution :
∆= (4)2-4(-1)
(1-m) = 20-4m
·
∆<0 20-4m<0 < = > m>5. =>.
Pas de solution dans IR
·
∆=0. 20-4m=0 < = > m=0. => Solution double
x0
= -4/2(-1) =2
·
∆>0 20-4m>0 < = > m<5 => Deux solutions distinctes.
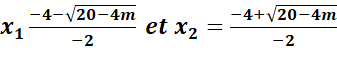
Équations irrationnelles
1.
On appelle équation irrationnelle, toute équation possédant un
radical (qui comporte le symbole Ѵ). Dans cette leçon, on se
limitera aux équations de la forme :
![]() où a, b, c et
d sont des réels.
où a, b, c et
d sont des réels.
2. Pour résoudre une équation irrationnelle, on commence par déterminer la/les
contrainte(s) et sous ces contraintes
on détermine la (ou les) solution(s) qui satisfont la contrainte.
3. Soit à résoudre l’équation :
![]() , elle se réduit au système :
, elle se réduit au système :
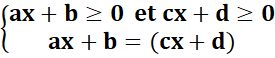
Remarque : La contrainte est indispensable lorsqu’il s’agit de
résoudre une équation irrationnelle
Exemple :
![]()
Solution : Il s’agit de résoudre ![]()
 . =>
. =>
![]()
Equations de degré supérieur ou égal
à 3.
Le programme suivant :
1. Déterminer une racine évidente α du polynôme P (x).
2. Trouver un polynôme q(x) de degré 2 tel que p(x)
= (x - α) q(x).
3. Résoudre les équations x - α = 0 et q(x) = 0 puis
déduire les solutions
Exemple1 :
Résoudre dans IR :
2x3+5x2-14x-8=0
Il faut d’abord chercher une racine évidente (…, -2,-1,0,1,
2…), ensuite choisir une des méthodes suivantes :
1ère méthode : Division
euclidienne
|
2x3. + 5x2. -14x-8. -(2x3-4x2) +9x2 -14x.
-(9x2-18x)
+4x-8
-4x+8 0 |
x-2
2x2+9x+4
|
=>2x3+5x2-14x-8=(x-2)( 2x2+9x+4)
2ème méthode : Déterminer les coefficients
a, b et c tels que :
2x3+5x2-14x-8=(x-2)(ax2+bx+c)
2x3+5x2-14x-8=ax3-2ax2+bx2-2bx+cx-2c
=ax3-(2a-b)x2-(2b-c)x-2c
Par identification, on a :

=>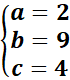
D’où 2x3+5x2-14x-8=(x-2)( 2x2+9x+4)
∆ =(9)2-4(2)(4)=81-32=49
x1=(-9-7)/4=-4
x2=(-9+7)/4=-1/2
Finalement, 2x3+5x2-14x-8=(x-2)( 2x2+9x+4)=2(x-2)(x+1/2)(x+4)=(x-2)(2x+1)(x+4)=0
S=
{-4,-1,2}
Équations bicarrées
On passe par un changement de variable.
Exemple :
Résoudre dans IR : x4+7x2-18=0
(équation bicarrée)
On pose X=x2, l’équation devient X2+7X-18=0
∆ =(7)2-4(1)(-18)=121
X1=(-7-11)/2 =-9
X2=(-7+11)/2 = 2
On sait que
X1=x2=-9
solution impossible car le carré ne peut pas être négatif
X1=x2=2 => x=-Ѵ2
et x=+Ѵ2 => S={-Ѵ2,+Ѵ2}
Equations rationnelles
C’est une équation dans
laquelle l’inconnue apparait au moins une fois au dénominateur d’une expression
et dont le domaine de définition n’est pas IR.
Exemple : Soit à résoudre :
![]()
Df=IR-{-3 ;3}
En mettant au même
dénominateur, on a :
![]() < = >
< = >![]()
![]()
∆ =(19)2-4(5)(102)=2401=(49)2
x1=(-19-49)/10=--34/5
x2=(-19+49)/10=3 exclue
EXERCICES
EXERCICE I :
1.a) Montrer
que le trinôme :
f(x)=2x2 +
3x +1 peut se mettre sous la forme
f(x)= 2[(x + ![]() )2 –
)2 – ![]() )]
)]
b) Comment appelle-t-on cette
forme ?
2) Déduire de l’expression de 1-b) les
solutions de l’équation f(x)=0.
On rappelle
l’identité remarquable :
a2-b2=
(a-b)(a+b).
3- Soit le polynôme de second degré P(x)=4x2-12x-7
a-
Donner
l’expression de la forme canonique de p(x)
b-
Utiliser
cette forme canonique pour trouver l’expression factorisée de p(x)
c-
En
déduire les solutions de l’équation p(x)=0.
EXERCICE II :
Résoudre dans IR, chacune des équations
suivantes et donner la forme factorisée des polynômes associés à chacune de ces
équations
a) -2x2
- Ѵ5x +
2 = 0,
b) 3x2
- 6x +
3 = 0,
c) 6x2
- 5x +
7 = 0.
d) -x2 +
|x|+
2 = 0,
e) (x -
10)2 - (x - 10)
- 2 = 0.
f) ![]() .
.
g) ![]() =x+4.
=x+4.
h) ![]() =x+10
=x+10
i)
x - 5Ѵx
- 6 = 0
EXERCICE III :
1. Soit m un paramètre réel.
Discuter et résoudre suivant les
valeurs de m l’équation (Em) :
-x2 + 4x +
1 - m = 0
2. Soit m un paramètre réel.
On considère l’équation d’inconnue x
:(Em) :
2x2 + m - x +
2 = 0
Discuter et résoudre suivant les valeurs de m, le nombre et le signe des
solutions de (Em)
EXERCICE IV : On donne les polynômes
p(x)
= x3 - x2 + x + 3 et q(x)
= 2x3 + 5x2 - 14x - 8
1.Vérifier que -1 est une racine évidente de p(x).
Vérifier que 2 est une racine évidente
de p(x).
2. Déterminer les autres racines de p(x)
et de q(x).
EXERCICE V :
1. a) Résoudre dans IR :
t4 -169t2 +3600 =0
b) En
déduire les solutions du système :
![]()
2. Résoudre
dans IR :
x4 +7x2 -18=0
EXERCICE VI :
1.Mme Ouattara a acheté un certain nombre de pièces de
tissu pour 43200frs. Si pour la même somme, elle avait eu 2 pièces de moins, la
pièce lui aurait couté 300frs de plus. Déterminer le nombre de pièces achetées
et le prix d’une pièce.
2.
Un commerçant achète n actions
dans une banque A à 600000 Fcfa.
Dans une autre banque B
il aurait pu acheter avec la même somme
100 actions en moins mais chaque action se verrait alors augmenter de
3000Fcfa. Déterminer le nombre d’actions
vendues et le prix d’une action
3.
De tous les rectangles d’aires
4.
Les élèves du Lycée classique de Bafoussam organise une excursion. Pour cela, ils
louent un car à120000f. Au moment du départ ,4 nouveaux élèves s’ajoutent et
chacun des partants doit alors payer 100f de moins.
Déterminer
le nombre d’élèves qui participent à l’excursion et la somme que chacun doit
payer.
EXERCICE VII :
1.
Une marchandise qui coutait 51840 FCFA
subit deux réductions de x%
puis est vendue au prix de 36000 FCFA. Déterminer la valeur de x.
2. Une usine de traitement de cacao,
permet de produire 7500 tonnes l’année de son ouverture qui est à sa 1ère
année de fonctionnement. Par suite de modernisation de son matériel, elle
augmente sa production de 1200 tonnes chaque année. Cette production se
poursuivra ainsi jusqu’à ce qu’elle atteigne une production maximale de 18300
tonnes.
La dépense D(x) où x désigne le nombre de jours est
donnée par
D(x)= -(1/2) x3+200x2 - 3000x.
1-Après combien
d’année, la production maximale sera atteinte ?
2-Pour quelle
valeur de x, le chef d’usine dépense-t-il minimum d’argent pour son
travail ?
CORRIGES
EXERCICE I :
1- a) Tout trinôme p(x) = ax2 + bx + c,
peut se mettre sous la forme p(x)= ![]()
f(x)= 2x2 + 3x +1 ,
Par identification a=2,
b=3 et c=1
=>![]() -4(2)(1)=1
-4(2)(1)=1
f(x) = 2[(x + 3/4)2
–1/16 )]
b)
forme canonique
2)
f(x)=0 < = >2[(x + 3/4 )2 – 1/16)]=0
<
= > 2[(x+3/4) -1/4][ (x+3/4) +1/4]=0
<=>2[x+1/2][ x+![]() ]=0
]=0
=>x=-1/2
ou x=-1.
3- Soit le polynôme de second degré P(x)=4x2-12x-7
A=4,b=-12,c=-7 et Δ=(-12)2-4(4)(-7) = 144+112=256
a- p(x) = 4[(x +(-12/8))2
–256/64] = 4[(x-3/2)2
-4]
b- p(x)= 4[x -3/2 -2] 4[x -3/2+2] =4[x-7/2 ] [x+1/2 ]
c-
p(x)=0 <=>4[x -7/2] [x +1/2]=o
=> x=7/2 ou x= -1/2
EXERCICE II :
a) -2x2 - Ѵ5x + 2 = 0
Δ=(-Ѵ5)2-4(-2)(2)=5+16=21
Δ>0 => cette équation admet deux
solutions distinctes
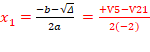 = -
= -![]()
 =
=![]() =>S = {
=>S = {![]() }
}
b) 3x2 - 6x + 3 = 0 < =>x2-2x+1=0
Δ=(-2)2-4(1)(1)=0
Δ=0 => cette équation
admet une solution double
x1=x2=-b/2a=-(-2/2)=1 =>S={1}
: //On pouvait remarquer
qu’on a l’identité remarquable (x-1)2 .
c) 6x2 - 5x + 7 = 0.
Δ=(-5)2-4(6)(7)=25-168=-143
Δ<0 => cette
équation n’admet pas de solution dans IR
S=![]()
d) -x2 + |x|+ 2 = 0 <=>(-x2+x+2=0) et (-x2-x+2=0)
·
-x2+x+2=0 pour x>0
Δ=(-1)2-4(-1)(2)=9 =>
x1= 2
x2= -1 exclu car x>0
·
-x2-x+2=0 pour x<0
Δ=(-1)2-4(-1)(2)=9 =>
x1=1 exclu car x<0
X=-2
S={-2 ;2}
g) ![]()
Contraintes : 7-2x ≥0 =>7≥2x =>x≤7/2
x+4![]() =>x
=>x![]() -4
-4
7-2x=![]() < = >x2 +10x+9=0 =>x1=
-9 et x2= -4
< = >x2 +10x+9=0 =>x1=
-9 et x2= -4
=>S={-4} // -9 est
exclu en tenant compte des contraintes
i) x - 5Ѵx - 6 = 0
On pose :X=Ѵx =>X2=x
L’équation devient : X2-5X-6=0
EXERCICE
III :
1-Discuter et résoudre suivant les valeurs de m l’équation (Em) :
-x2 + 4x +
1 - m = 0
Δ=(4)2-4(-1)(1-m)=16+4(1-m)=20-4m
Δ<0 <=>20-4m<0 d0nc m>5 =>S=![]()
Δ=0 <=>20-4m=0
donc m=5
=> S=-2
Δ>0<=>20-4m>0 donc m>5 =>
x1=![]() et x2=
et x2=![]()
EXERCICE
IV :
1. On donne les polynômes
p(x) = x3
- x2 + x + 3 et q(x) = 2x3
+ 5x2 - 14x - 8
p(-1)=(-1)3 –(-1)2+(-1)+3=-1-1-1+3=0
q(2)=2(2)3
+5(2)2 -14(2) -8=16+20-28-8=0
2. Déterminer les autres racines de p(x)
et de q(x).
p(x)=(x+1)(ax2 +bx
+c)
= ax3 +(b+a)x2+(b+c)x +c or p(x) = x3 - x2
+ x + 3
On obtient par identification :
 =>b=-2 et c=3
=>b=-2 et c=3
p(x) devient p(x)=(x+1)(x2 -2x +3)
p(x)=0 <=> (x+1)(x2 -2x
+3)=0 =>(x+1=0) ou (x2-2x+3=0)
=>S={-1} car x2 -2x +3=0 n’a pas de
solution dans IR
q(x)=(x-2)(ax2 +bx +c)
= ax3 +(b-2a)x2+(c-2b)x +=-2c or q(x) = 2x3 + 5x2
- 14x - 8
On obtient par identification:
 =>b=9 et c=4
=>b=9 et c=4
p(x) devient p(x)=(x-2)(2x2 +9x +4)
p(x)=0 <=> (x-2)(2x2
+9x +4)=0
=>(x-2=0)ou(2x2+9x+4=0)
=>S={-4 ;![]() ;2}
;2}
//autre méthode :
|
x3 - x2
+ x + 3 -x3-x2 2x2+2x 3x+3 -3x-3 |
X+1 |
|
X2 -2x +3 |
EXERCICE V :
1. a) Résoudre dans IR : t4
-169t2 +3600 =0
On pose : x=t2
L’équation devient :x2 -169x
+3600=0
Δ=(-169)2-4(1)(3600)
=28561-14400=14161
=(119)2
x1=25
x2=144
On revient sur l’inconnu
auxiliaire x= t2
t2=25 =>
t=-5 ou+5
t2=144 =>t=-12 ou+12
=> S={-12,-5,5,12}
b)
En déduire les solutions du système :
![]()
![]()
x2+(60/x)2=169 <=> x4
-169x2 +3600=0
On retrouve l’équation de
a)
=> S={(-5 ;-12) ; (-12 ;-5) ;
(5 ;12) ; (12 ;5) }
//autre méthode :
x2+y2=(x+y)2-2xy=(x+)2-120
On aboutit aux systèmes![]() =>
=>![]()
EXERCICE VI :
1.Soient : x : nombre de pièces
y : prix d’une pièce
![]()
xy=43200 => y=43200/x => (x-2)( 43200/x +300)=43200
ou x2-2x-288=0
On trouve x1=-16
et x2=18
La solution négative est exclue
La solution acceptable est x=18 et y=2400
3. Soient :
x : longueur
y :
largeur
![]()
On trouve par substitution :
y=100/x =>P=2(x+100/x)
d’où :
x2 - (P/2)x+100 = 0
Δ= P2/4– 400
Δ≥0 => P2/4– 400 ≥0
=>P≥40
La plus petite valeur est atteinte lorsque
P=40 (![]() ) x=y=10 donc le rectangle de périmètre
minimal est un carre.
) x=y=10 donc le rectangle de périmètre
minimal est un carre.
4. Les élèves du Lycée classique de Bafoussam organise une excursion.
Pour cela, ils louent un car à120000f. Au moment du départ ,4 nouveaux élèves
s’ajoutent et chacun des partants doit alors payer 100f de moins.
Déterminer le nombre d’élèves qui participent à l’excursion et la somme
que chacun doit payer.
Soient : x : nombre initial de
participant
y : la somme initiale
![]()
xy=120000 =>y=120000/x => x2+400x-480=0
On trouve x1= -24 et x2=
20
La solution négative est exclue
La solution acceptable est x=20 et y=6000
Donc au départ 20 élèves se sont inscrits
pour l’excursion et chacun devait payer 6000frs. Avec l’arrivée des 4 derniers
élèves, l’excursion compte désormais 24 participants et chacun doit payer
5000frs.
EXERCICE IX :
1.
x1+x2=7/5
=>x2=7/5-1=2/5
2.
S=60 et P=864 => x2-60x+864=0
S= {24,36}
Avez-vous
un exercice a proposer?Cliquez-ici
Merci de votre visite
Laissez un commentaire