LA LUMIERE
DISPERSION
DE LA LUMIERE
Lumière simple-lumière complexe
·
Une
lumière indécomposable est une lumière simple ou monochromatique ;
elle constitue une radiation lumineuse.
Exemple : Lumière du sodium obtenue en éclairant
une fente avec une lampe à vapeur de sodium (couleur jaune uniquement).
·
Une
lumière décomposable en plusieurs radiations simples est une lumière
complexe ou polychromatique.
Exemple : La lumière blanche est le résultat de
la superposition de plusieurs couleurs (sept couleurs). C’est une lumière polychromatique.
//chroma=couleur
La lumière
blanche contient une infinité de radiations, émises simultanément par la source
et qui se propage le long des mêmes rayons incidents.
Définition :
On
appelle dispersion de la lumière un phénomène optique qui se produit
lorsque la lumière complexe est séparée en ses couleurs constituantes, comme le
montre le passage de la lumière à travers un prisme.
Un
prisme par exemple décompose la lumière blanche (lumière solaire) en sept
radiations monochromatiques. L’ensemble de ces radiations observées sur un
écran constitue le spectre de la lumière blanche. On obtient les sept
couleurs de l’arc-en-ciel : le rouge, l’orangé, le jaune, le vert,
le bleu, l’indigo et le violet par ordre de déviation croissante.

Spectre de la lumière blanche
L’indice
de réfraction d’un milieu transparent varie avec la lumière qui se réfracte
L’indice
de réfraction d’un milieu varie avec la radiation qui se réfracte. La déviation
due aux deux réfractions successives sur les faces d’un prisme augmente avec
l’indice du prisme :
Dj<Dv<Db
L’indice va
croissant du jaune au bleu.
De
même, la dispersion de la lumière blanche par le prisme montre que l’indice du
prisme augmente insensiblement d’une radiation a la suivante, depuis la
radiation rouge extrême jusqu’à la radiation violette extrême.
Pour
le verre, les indices correspondants aux sept couleurs de l’arc-en-ciel se
classent dans l’ordre suivant :
nr<no<nj<nv<nb<ni<nvi
En résumé, les diverses
radiations lumineuses contenues dans la lumière complexe se distinguent :
-physiologiquement
par les couleurs différentes
-physiquement
par les réfractions différentes au passage d’un milieu transparent a un autre.
Spectre d’émission-spectre d’absorption
Spectre
d’émission
Définition
Le
spectre d’émission est l’ensemble des radiations lumineuses émises par une
source lorsqu’elle est excitée (chauffée, soumise à une décharge électrique,
etc.). C’est le rayonnement émis par une substance lorsqu’elle passe d’un état
excité à un état stable.
Deux types de
spectres d’émission :
Spectre
continu
Le
spectre d’émission peut être continu s’il est possible de passer
d’une radiation a une autre sans interruption (cas de la lumière blanche).

Spectre de la lumière
Il
peut être produit par un corps chaud (comme une lampe à incandescence, le
Soleil…).
Toutes les
longueurs d’onde sont présentes, sans interruption (un dégradé de couleurs du
violet au rouge).
Spectre de
raies (ou spectre discontinu)
Un
spectre est discontinu s’il est formé d’un nombre fini d’images bien
séparées, chacune d’elle correspondant à une radiation déterminée de la lumière
incidente (cas de la lampe à vapeur de sodium). Les raies d’un tel spectre sont
caractéristiques de l’élément chimique qui émet la lumière étudiée.

Un
spectre discontinu est produit par un gaz excité (ex : vapeur de mercure ou de
sodium).
On
observe uniquement quelques raies colorées sur fond noir.
Chaque
élément chimique a son propre spectre de raies.
Utilité :
-
Identifier une substance à partir de ses raies d’émission.
-
Étudier la composition des étoiles ou des gaz.
NB : Les raies d’un spectre discontinu sont
caractéristiques de l’élément chimique qui émet la lumière étudiée ; elles
dépendent de la structure des atomes de cet élément. L’identification des
radiations lumineuses qui correspondent à ces raies permet donc de reconnaitre
l’élément qui les émet : c’est le principe de l’analyse spectrale.
Elle
se fait à l’aide d’un spectroscope.
Spectre
d’absorption
Définition :
Le
spectre d’absorption est l’ensemble des radiations (longueurs d’onde) qu’un
corps absorbe dans un rayonnement incident.
Exemple :
Si
on laisse passer la lumière blanche dans la vapeur de sodium, on constate que
le spectre d’absorption formé présente une raie noire à la place de la raie
jaune précédente : la vapeur de sodium a uniquement absorbé la radiation
jaune. Cette absorption est sélective.
Présentation
:
-
Sur un spectre lumineux, on observe un fond continu (comme celui de la lumière
blanche),
-
Avec des lignes noires (raies d’absorption) ou des creux qui correspondent aux
longueurs d’onde absorbées.
Exemple :
- La
lumière du Soleil, en traversant l’atmosphère ou la surface du Soleil, donne un
spectre avec des raies noires (raies de Fraunhofer) : c’est un spectre
d’absorption.
Utilité :
-
Identifier les éléments chimiques présents dans une substance (chaque élément a
un spectre d’absorption unique),
-
Étudier des étoiles, des gaz, ou des solutions en laboratoire.
Conclusion :
-Le spectre
d’émission montre ce que la matière émet, tandis que le spectre d’absorption
montre ce qu’elle absorbe.
-Un spectre
d’absorption est le négatif du spectre d’émission : il indique ce qui manque
dans la lumière après passage dans une substance.
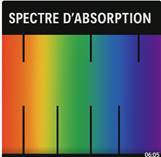
|
Cette image montre un spectre d’absorption,
caractérisé par un fond coloré continu (comme l’arc-en-ciel, allant du rouge au violet),
interrompu par des raies noires. |
- Les raies noires correspondent aux longueurs
d’onde de la lumière absorbées par une substance (souvent un gaz entre la
source lumineuse et l'observateur). - Chaque élément chimique produit un spectre
d’absorption unique, ce qui permet de l’identifier (utilisé en astrophysique,
chimie analytique…). - Le fond continu est typique d’une source chaude
(comme le Soleil), tandis que les raies sont dues à des couches de gaz plus
froides qui absorbent certaines longueurs d’onde spécifiques. C’est l’inverse du spectre d’émission, où les
raies apparaissent colorées sur fond noir. |
La
recomposition de la lumière blanche
Les radiations
lumineuses obtenues par dispersion redonnent la lumière complexe initiale
lorsqu’on les superpose.
MODELE ONDULATOIRE DE LA LUMIERE
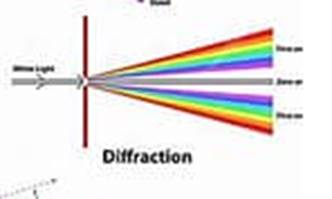
Diffraction de la lumière.
Le
phénomène de diffraction apparaît lorsqu’on cherche à isoler un rayon lumineux
à partir d’une source étendue.
Pour cela, on
fait passer la lumière à travers un diaphragme et on la reçoit sur un écran.
Quand le diamètre du diaphragme devient très petit (de l’ordre du 10ème
du millimètre), le trou se comporte comme une source et envoie la lumière dans
toutes les directions, on dit que l’on a obtenu le phénomène de diffraction.

On
peut représenter la lumière comme une onde qui se propage. On
parlera d’une onde lumineuse caractérisée par une période T et pouvant
se propager à une vitesse v dans un milieu de propagation donné.
Dans
le vide par exemple, la lumière se propage avec une vitesse c (célérité).
c = 3x108m/s.
Longueur d’onde d’une radiation lumineuse
C’est
la distance parcourue par une onde lumineuse pendant une période. Elle est
notée λ et s’exprime en mètre (m).
λ=c.T
c est la célérité de la lumière en mètres par
seconde(m/s)
T est la période en seconde (s)
λ est la longueur d’onde en mètres (m)
NB : Une lumière polychromatique est
constituée d’un grand nombre de radiations de longueurs d’onde différentes.
Spectre électromagnétique de la lumière
Les
ondes lumineuses appartiennent à un ensemble d’ondes ayant les mêmes propriétés
appelées ondes électromagnétiques
 .
.
Exemple ; lumière visible est dans un
intervalle compris entre 400 nm et 780 nm. L’œil est sensible aux radiations de
longueur d’ondes comprise entre cet intervalle.
Couleurs des corps chauffés (loi de Wien)
Lorsqu’un
corps est réchauffé, il émet de la lumière : c’est ce qu’on appelle le rayonnement
thermique.
Émission
continue liée à la température
- Un corps chauffé émet un spectre continu de
lumière, sans discontinuité.
- La couleur émise dépend de la température
du corps :
- Température basse : rouge sombre.
- Température moyenne : orange, jaune.
- Haute température : blanc, puis bleu clair.
Exemples
- Un métal
chauffé rougit, puis jaunit, puis devient blanc (ex. filament de lampe).
- Le Soleil (≈
5800 K) émet une lumière blanche, car son spectre couvre tout le visible.
La loi de Wien
décrit la relation liant la longueur d’onde λmax
correspondant au pic d’émission d’un corps et la température absolue T :
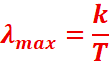
λmax : longueur d'onde correspondant à l'intensité
maximale du rayonnement émis en m ;
T: température de surface du corps en K ;
k : constante de Wien.
k=2,89777291x10-3
m.K
Loi de Wien : La longueur d’onde maximale émise est inversement
proportionnelle à la température.
Il découle de cette loi que plus un objet est chaud, plus la
longueur d'onde du rayonnement émis le plus intensément est courte. Plus le corps est chaud, plus la lumière émise est
riche en courtes longueurs d’onde (bleu-violet).
Application :
Un corps noir émet un maximum d’intensité lumineuse à la longueur d’onde λmax = 500 nm.
Constante de Wien : b = 2,9 × 10⁻³ m·K
Calculons la température T de ce corps.
La loi de Wien s’écrit :
T = b / λmax
Convertissons λmax en mètres
:
λ_max = 500 nm =
500 × 10⁻⁹ m = 5,0 × 10⁻⁷ m
Calcul :
T = 2,9 × 10⁻³ / 5,0 × 10⁻⁷ = 5800 K
Profil spectral
d’une source lumineuse
Le
profil spectral d’une onde lumineuse désigne la répartition de l’intensité de
la lumière en fonction des longueurs d’onde (ou des fréquences) qu’elle
contient.

Profil
spectral de l’etoile71 Tauri
En d'autres
termes :
C’est une
courbe ou un graphique qui montre quelles couleurs (ou radiations) composent la
lumière, et quelle est l’intensité de chacune d’elles.
Exemple :
- Une lumière
blanche (comme celle du Soleil) a un profil spectral continu, avec toutes les
longueurs d’onde visibles (du violet au rouge).
- Une lampe à
vapeur de sodium a un profil spectral discret, avec des pics très nets à
certaines longueurs d’onde (typiquement dans le jaune).
Utilité :
Le profil
spectral permet :
- d’identifier
une source lumineuse (signature spectrale),
- d’analyser la
composition chimique d’un corps (ex. : étoiles, gaz),
- de déterminer
des températures, vitesses, etc.
MODELE CORPUSCULAIRE DE LA LUMIERE : LE PHOTON
Pour interpréter certains phénomènes
physiques (effet photoélectrique), ALBERT EINSTEIN considère que :
·
La
lumière est constituée de particules de charge et de masse nulle appelées
photons se propageant à la vitesse de la lumière.
·
Chaque
photon transporte une énergie propre ou quantum d’énergie de valeur :
E = hυ
υ
est la fréquence du rayonnement
h=6,62.10-34J/s une constante appelée constante de
Planck.
Dualité
onde-corpuscule
La
lumière se présente sous deux aspects :
-Un
aspect ondulatoire : où elle est considérée comme un phénomène vibratoire se
propageant par une onde.
-Un
aspect corpusculaire : où elle est formée de corpuscules appelés photons qui
sont animés d’une vitesse c (célérité de la lumière) et transportant un quantum
d’énergie E tel que E = hυ.
EXERCICES
EXERCICE
I :
Un faisceau de lumière blanche traverse un prisme en
verre placé dans l’air.
1.On observe une bande colorée en sortie.
1,1-Que se passe-t-il lorsque la lumière blanche
traverse le prisme ?
1.2- Quelles couleurs observe-t-on dans l’ordre
?
1.3- Comment appelle-t-on ce phénomène ?
2.Un prisme dévie les différentes couleurs de la lumière blanche.
2.1. Quelle couleur est la plus déviée ?
2.2. Quelle est la couleur la moins déviée ?
2.3. Pourquoi les couleurs sont-elles déviées
différemment par le prisme
3.La lumière du Soleil est décomposée par un prisme. Le spectre est
continu, mais il comporte de nombreuses raies noires.
3.1. Quel type de spectre est-ce ?
3.2. Que représentent les raies noires dans ce
spectre ?
3.3. Que peut-on déduire sur la composition de
l’atmosphère du Soleil ?
EXERCICE II : Identifier
le type de spectre
1.On observe trois spectres lumineux différents à l’aide d’un
spectroscope :
- Spectre A : un fond noir avec quelques raies colorées.
- Spectre B : un fond coloré continu sans interruption.
- Spectre C : un fond coloré avec quelques raies noires.
11. Quel type de spectre est A ?
1.2. Quel type de spectre est B ?
1.3. Quel type de spectre est C ?
1.4. Quelle est l'origine physique de chaque spectre
?
2.Un gaz chauffé émet de la lumière. On observe son spectre
d’émission.
On éclaire ensuite ce même gaz avec de la lumière blanche et on observe à
nouveau un spectre.
2.1. Quel type de spectre observe-t-on dans le
premier cas ?
2,2. Quel type observe-t-on dans le second cas
?
2.3. Que remarque-t-on en comparant les deux
spectres ?
2,4. Que peut-on conclure sur les raies d’absorption
et d’émission d’un gaz ?
3.Un astronome observe le spectre lumineux d’une étoile.
Ce spectre est continu avec plusieurs raies noires fines.
3.1. Quel type de spectre est observé ?
3.2. Que signifient les raies noires dans le spectre
?
3.3. Que peut-on déduire sur la composition de
l’atmosphère de l’étoile ?
3.4. Pourquoi le spectre est-il utile pour
identifier les éléments présents dans l’étoile ?
EXERCICES III :
1.On observe à l’aide d’un spectroscope :
- Cas A : un fond noir avec des raies colorées fines.
- Cas B : un fond coloré continu avec des raies noires.
1.1. Quel type de spectre observe-t-on dans chaque cas ?
1.2. Quelle est la nature de la source lumineuse dans chaque cas ?
1.3. Quelle information peut-on tirer sur la composition de la matière
dans chaque cas ?
2.Une lampe contenant du gaz d’hydrogène émet de la lumière analysée par
un spectroscope.
On observe 3 raies : rouge, bleue et violette.
2.1. Quel type de spectre est observé ?
2.2. Pourquoi observe-t-on seulement quelques raies ?
2.3. Que peut-on conclure sur l’origine de ces raies ?
EXERCICE
IV :
1.Un corps
porté à la température T= 4830 K, émet ainsi de l'énergie sous forme de
lumière.
1.1- Déterminer la longueur
d'onde maximale et déduire la couleur de la lumière émise.
1.2- En supposant que la
longueur d'onde λ=5,98×10−7 m, déterminer la
fréquence et l'énergie en eV de la lumière émise par ce feu d'artifice
On donne: C=3×108 m/s , h=6,63×10−34 J.s, 1eV=1,6×10−19 J.
On rappelle la loi de Wien : λ.T=2,898 ×10−3 m.K
|
Couleur |
Violet |
Bleu |
Vert |
Jaune |
Orange |
Rouge |
|
Domaine de longueur d'onde
(nm) |
380 - 446 |
446 - 520 |
520 - 565 |
565 - 590 |
590 - 625 |
625 - 780 |
2.Lorsque
la Terre reçoit les rayons solaires, sa température moyenne est de 293 K. On
admet que la Terre obéit à la loi de Wien.
2.1. Calculer la longueur
d'onde du maximum de rayonnement émis par la Terre.

2.2. Donner le domaine des ondes
émises par la Terre sachant que λmax=9,89×10−6
m
EXERCICE
V :
1.Une lampe à
vapeur de sodium émet une radiation de fréquence f=5,09×1014
Hz. Calculer :
1.1 L'énergie de cette
radiation.
1.2 La longueur d'onde de
cette radiation.
2.Déterminer
l’énergie en Joules et en électronvolt (eV) d’un photon issu d’un pointeur
laser de longueur d’onde λ=650nm.
Données : c=3×108 m/s; h=6,62×10−34 J.s ; 1eV=1,6×10−19 J ; 1nm=10−9 m.
EXERCICE VI :
1.
Un corps noir émet un maximum d’intensité lumineuse à la longueur d’onde
λ_max = 500 nm.
Calculez la température T de ce corps.
(Constante de Wien : b = 2,9 × 10⁻³ m·K)
2.
Le Soleil a une température d’environ 6000 K.
Quelle est la longueur d’onde λ_max
correspondant à l’émission maximale du Soleil ?
3.
Un four industriel émet un maximum d’intensité à λ_max
= 1,45 μm.
Calculez la température T du four.
EXERCICES VII :
1.Une étoile émet un maximum d’intensité lumineuse à 700 nm. Quelle est
sa température de surface ?
Données :
b = 2,9 × 10⁻³ m·K
λ_max = 700 nm =
7,0 × 10⁻⁷ m
2.Un corps chauffé dégage un rayonnement dont le maximum est à 400 nm.
Quelle est sa température ?
3.La température d’un corps noir est de 3500 K. Calculez la longueur
d’onde du maximum d’émission.
CORRIGES
EXERCICE
I :
1.1. Elle est
décomposée en plusieurs couleurs.
1.2. Rouge, orange, jaune, vert, bleu, indigo,
violet (souvent abrégé ROJVIBV).
1.3. La dispersion de la lumière.
2.1 Le violet.
2.2. Le
rouge.
2.3. Car chaque couleur a une longueur d’onde
différente.
Le prisme dévie davantage les courtes longueurs
d’onde (comme le violet) que les longues (comme le rouge).
C’est ce qu’on appelle la réfraction dépendante de
la longueur d’onde.
3.1. C’est un spectre d’absorption.
3.2. Les raies noires sont dues à l’absorption de
certaines longueurs d’onde par les éléments présents dans l’atmosphère solaire.
3.3. Cela permet d’identifier les éléments chimiques
présents dans l’atmosphère du Soleil (ex : Hélium, Sodium...)
EXERCICE II :
1.1. Spectre A : Spectre discontinu ou Spectre de raies → produit par un gaz excité à basse
pression.
1.2. Spectre B : Spectre continu → produit par
un corps chaud (ex. filament de lampe).
13. Spectre C : Spectre d’absorption → produit
lorsqu’une lumière blanche traverse un gaz froid.
1.4. Origine physique :
- Spectre
discontinu ou Spectre de raies : atomes isolés qui émettent à des longueurs
d’onde précises.
- Spectre
continu : rayonnement thermique d’un corps chaud dense.
-
Absorption : atomes absorbent certaines longueurs d’onde du spectre continu.
2.1. Premier cas : spectre d’émission de raies (gaz
chauffé).
2.2. Second cas : spectre d’absorption (gaz éclairé
par lumière blanche).
2.3. Remarque : les raies noires du spectre
d’absorption correspondent exactement aux raies colorées du spectre
d’émission.
2.4. Conclusion : un gaz absorbe les mêmes longueurs
d’onde qu’il peut émettre → chaque élément chimique a une signature
spectrale unique.
3.1. Spectre observé : spectre d’absorption.
3.2. Raies noires : elles correspondent à des
longueurs d’onde absorbées par les éléments présents dans l’atmosphère de
l’étoile.
3.3. Conclusion : les raies permettent d’identifier
les éléments chimiques présents.
3.4. Utilité : grâce au spectre, on peut faire une
analyse chimique à distance de l’étoile sans contact direct
EXERCICES III :
1.1.
- Cas A : Spectre d’émission de raies.
- Cas B : Spectre d’absorption.
1.2.
- Cas A : Émis par un gaz excité à basse
pression.
- Cas B : Issu d’une source lumineuse blanche
traversant un gaz (atmosphère du Soleil par exemple).
1.3.
- Chaque spectre est caractéristique d’un élément
chimique, donc permet d’identifier la composition du gaz ou de l’atmosphère
traversée.
.21. C’est un spectre d’émission de raies.
2.2. Les raies observées correspondent aux
transitions électroniques entre niveaux d’énergie quantifiés. Les électrons ne
peuvent passer que par certains niveaux.
3.3. Chaque raie correspond à une énergie émise
spécifique → signature de l’atome d’hydrogène
EXERCICE
IV :
1.
1.1 longueur d'onde max
λmax.T=2,898 ×10−3 <
=>λx4830=2,898 ×10−3 => λmax=600 nm
La
lumière émise est de couleur orange
1.2 Calcul de la fréquence
![]() =
=![]() =
=![]()
Calcul
de l’Énergie
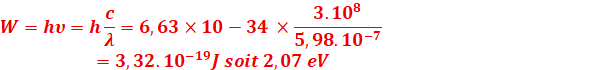
2.
1- Longueur d'onde du maximum de rayonnement émis par la Terre.
λmax.T=2,898 ×10−3 <
=>λmaxx293=2,898 ×10−3 => λmax=9,89.10-6 m
2.2-
le domaine des ondes émises par la Terre sachant que λmax=9,89×10−6
m est dans l’infrarouge
EXERCICE
V :
1.
1.1 L'énergie de cette radiation.
W=hf=6,62×10−34 x5,09×1014=33,7.10-20
J
1.2 La longueur d'onde de cette radiation.
![]()
2.Energie
en Joules et en électronvolt (eV) d’un photon
![]()
Soit : ![]()
EXERCICE VI :
1. Loi de Wien : T = b / λ_max
- λ_max = 500 nm =
500 × 10⁻⁹
m
- T = 2,9 × 10⁻³
/ (500 × 10⁻⁹)
= 5800 K
2. λ_max = b / T =
2,9 × 10⁻³
/ 6000 = 4,83 × 10⁻⁷
m = 483 nm (visible bleu-vert…
3.T=2,9 × 10⁻³
/ 1,45.10-6 =2000K
La température
du four est environ 2000 kelvins.
EXERCICE VII :
1.λ_max = b / T → T = b / λ_max
T = 2,9 × 10⁻³
/ 7,0 × 10⁻⁷
= 4142,9 K
La température de surface de l’étoile est environ
4143 K.
2.T = b / λ_max = 2,9
× 10⁻³
/ 4,0 × 10⁻⁷
= 7250 K
La température du corps est 7250 K.
3.T = 3500 K
λ_max
= b / T = 2,9 × 10⁻³
/ 3500 = 8,29 × 10⁻⁷
m = 829 nm
La longueur d’onde du maximum d’émission est environ
829 nm (dans l’infrarouge proche).
Merci de votre visite
Laissez
un commentaire