FORCES ELECTROSTATIQUES : LOI DE COULOMB


FORCES ELECTROSTATIQUES
Mise en évidence

 

Enoncé de la loi de Coulomb :

La force d’attraction ou de répulsion qui s’exerce entre deux charges ponctuelles qA et qB, placées respectivement aux points A et B distants de d, est proportionnelle à qA et qB et inversement proportionnelle au carré de la distance qui sépare les deux charges.

Caractéristiques

 


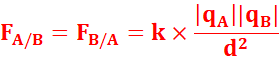
qA et qB en coulombs( C)

d en mètres ( m)

K=9.109 SI

F en newton (N)

 

 

CHAMPS ELECTROSTATIQUES
Définition :
                       C’est une région de l’espace où toute charge électrique q est soumise à une force électrostatique. Le champ électrostatique noté  est donné par la relation :

 


Caractéristiques


 

 

 

Champ uniforme

          Un champ électrique est uniforme dans une région de l’espace si le vecteur champ électrique est constant (direction, sens et intensité) en tous les points de cet espace.


Cas d’un condensateur plan :

            Un condensateur plan est constitué de deux plaques A et B séparées par une distance d. Lorsque le condensateur est chargé, il y a production d’un champ électrique uniforme .

 

 

 

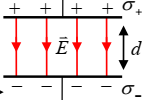
La production d’un champ électrique implique obligatoirement la production d’une différence de potentiel (ddp) entre les deux plaques. Elle peut être évaluée grâce à l’expression suivante :

 

                                                                                 

 

UAB est la ddp entre les armatures du condensateur en volts

d est la distance entre les armatures du condensateur en mètre

E est le champ électrique en volts par mètre

 

EXERCICES

EXERCICE  I:

1.Calculer la force d’attraction d’origine électrique qui s’exerce entre le noyau et l’électron dans l’atome d’hydrogène. L’électron est supposé tourner autour du noyau suivant une circonférence de rayon r0=53,3x10-12 m. La charge de l’électron est e=1,6x10-19 C.

2.Une charge ponctuelle de -10-6 C est placée en un point O d’un axe Ox.

a-Trouver la valeur de la charge qu’il faut placer en un point M, tel que OM=5cm, pour que ces deux charges exercent une force répulsive d’intensité F=3,6N.

b-Calculer la valeur du champ électrique qui règne en ce lieu.

EXERCICE II :

Deux charges électrostatiques ponctuelles q1 et q2 sont placées respectivement aux points A et B, distants de 10 cm. On donne q1 = -10-8 C ; q2 =+10-8 C ; k=9.109 USI.

1.Représenter sur un schéma la force électrique  à la quelle est soumise la charge q2, puis calculer son intensité.

2. Quel est l’ensemble des positions qu’occuperait q2 dans le plan de la figure, pour que    ait la même intensité que celle calculée ci-dessus ?

3.Soit M, un point de la médiatrice du segment [AB], tel que l’angle ( )= Ѳ =60°

3.1 – Représenter les champs E1 et E2 respectivement créés en M par q1 et q2, puis construire leur somme  .

3.2- Sachant que E1=E2=9.10-9 N.C-1 , calculer la norme de .

 

EXERCICE III :

Au sommet d’un triangle ABC isocèle en A, on place respectivement les charges qA = 10 nC ; qB = -5 nC ; qC =2 nC.
Soit  M un point situé au milieu de BC.

 AB = 2cm et BC = 1,5cm.
1. Calculer le champ E1 créé par la charge qA au point M.

2. a) Calculer le champ EM1 créé par la charge qB au point M.

    b) Calculer le champ EM2 créé par la charge qC au point M.

    c) En déduire le champ total crée par les charges qB  et qC en M.

4. Calculer le champ résultant au point M.

.

 

 

EXERCICE IV :

Entre les plaques métalliques parallèles et horizontales d’un oscillographe existe un champ
électrostatique uniforme d’intensité E = 2000V/m. La plaque supérieure est chargée positivement.
1. Sur un schéma, représente le vecteur champ    et les forces appliquées à un électron se trouvant en
un point de ce champ.
2. Compare les intensités de ces forces. Conclus.
Données : e = 1,6.10-19 C ; m = 9,1.10-31 kg ; g = 10N/kg.

EXERCICE V :
1-Calcule la valeur F de la force électrostatique   subie par un électron se trouvant dans un champ
électrostatique de valeur E =100 V/m.
2-Compare cette valeur au poids P de l’électron
3-Conclus
Données : Électron : me = 9,1.10-31 kg ; q= -e = -1,6.10-19 C ; g =10 N/kg.

 

EXERCICES VI :

On considère une goutte d’huile électrisée dont le rayon a pour valeur 1,09.10-3 cm. La masse volumique de l’huile est de 0,9 g/cm3. Cette goutte d’huile est placée entre deux plaques métalliques parallèles et horizontales. La ddp entre ces plaques est de 6000 V et leur distance de 2 cm. On constate que la goutte est en équilibre.

1.Quelle est, des deux plaques, celle dont le potentiel est plus élevé ?   

2.Quelle est la valeur de cette charge ?

 

EXERCICE VII : 

Trois charges ponctuelles A, B, C de charges qA = -2.10-7 C, qB = 4.10-7 C et qC= 3.10-7 C sont placées au sommet d’un triangle équilatéral ABC de coté 4 cm.

 On donne  k=1/4πЄ0 =9.109 uSI.

1.Calculer le module de la force que qA exerce sur qC et le module de la force que qB exerce sur qC.

2.Faire un schéma montrant les deux forces calculées et en déduire graphiquement le module F de leur résultante. Indiquer l’échelle utilisée.

3.Déduire de la question précédente l’intensité E du champ électrique créé en C par les charges placées en A et B.

 

 

 



EXERCICES

EXERCICE I:

1. Calculons la force d’attraction

 

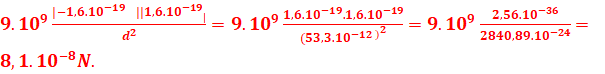
2.

a)   =

b) .

 

EXERCICE II :

1.   Représentation de la force

= ==

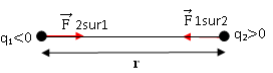
2. Soit x cette position,

 =

x2=10 (cm)

L’ensemble des points est un cercle de centre A de rayon 10 cm.

3.

3.1)

3.2) E1=E2=9.10-9 N.C-1  => on a un losange, donc les diagonales sont perpendiculaires.

L’angle entre E et E1 est 60° car Les angles ( ) et ( ) sont semblables.

E=2E1cos60=2x9.10-9cos60=15,6.10-9 NC-1

 

EXERCICE III :
1. Champ E1 créé par la charge qA au point M.

Plaçons une charge +q en M.

Le triangle AMB est rectangle en M donc AM2 + MB2=AB2  => AM=1,85.10-2 m.

===.

 

1.   a) Champ EM1 créé par la charge qA au point M.

Le point M est au milieu de BC , BM=BC/2=1,5/2=0,75cm

 

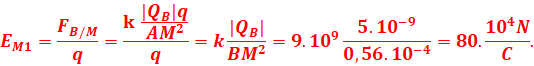
b) Champ EM2 créé par la charge qA au point M.

 

Le point M est au milieu de BC, CM=BC/2=1,5/2=0,75 cm

 

 

 

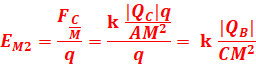
c)E2= EM1-EM2=(80-32)104=48.104 N/C

4. Champ résultant au point M.

E2=E12 +E22 =>

 

EXERCICE IV :
1.


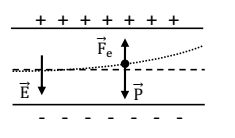
2.

 Fe = 3,5.1013 P

 P est négligeable devant Fe

EXERCICE V :

1- F = |q|.E = 1,6.10-19 x 100 =1,6.10-17 N
2- P = mg = 9,1.10-30 N F
P
= 175.1010 F = 175.1010 P
3- P négligeable devant F.

 

EXERCICES VI :

1.La plaque supérieure est au potentiel le plus élevé.

2. La goutte est en équilibre : -qE=mg => q=-mg/E

E=U/d  et m=ρV=ρ4πr3/3

 

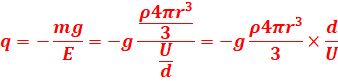
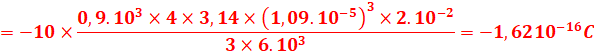
EXERCICE VII : 

 

1.Force exercée entre qA et qC

 

Force exercée entre qB et qC

 

2.

Avez-vous un exercice à proposer ?Cliquez-ici

Merci de votre visite
Laissez un commentaire