LA MASSE D’UN CORPS, SA RELATION AVEC LE POIDS

Le poids

Le poids d’un corps est la force d’attraction que la terre exerce sur ce corps.

Il est représenté par la lettre.

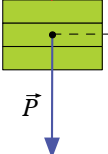
Le poids d’un corps est une force repartie que l’on remplace dans la pratique par une force unique dont les caractéristiques sont :

· Direction : verticale.

· Sens : descendant, du haut vers le bas.

· Point d’application : au centre de gravité G du corps.

· Intensité : mesure indiquée par le dynamomètre. Elle s’exprime en newtons(N)

La masse

La masse d’un corps représente la quantité de matière que contient ce corps. On la mesure à l’aide d’une balance.

Dans le système international, l’unité de masse est le kilogramme (kg).

La masse d’un corps est une grandeur scalaire. Elle est indépendante du lieu et de l’état physique dans lequel le corps se trouve.

La relation entre le poids et la masse

L’expérience montre que le poids d’un corps est proportionnel à sa masse.

On écrit :

P=mg

P en newtons(N)

m en kilogramme (kg)

g en newtons par kilogramme (N/kg)

g= 9,81 N/kg est l’intensité de la pesanteur.

La constante g de proportionnalité, dépend du lieu où on réalise l’expérience. A titre d’exemple, notons que l’intensité de la pesanteur au pôle nord est g=9,83N/kg et qu’à l’équateur elle est g=9,78N/kg

La masse volumique, le poids volumique, la densité

La masse volumique

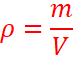
La masse volumique d’un corps est la masse de l’unité de ce corps. Elle est égale au rapport de la masse d’un échantillon de ce corps à son volume.

m en kilogrammes (kg)

V en mètres cubes (m3)

ρ en kilogrammes par mètres cube (kg/m3)

Le poids volumique

Le poids volumique d’un corps est le poids de l’unité de volume de ce corps.

ϖ = =ρg

ϖ s’exprime en newtons par m³ (N/m³)

La densité d’un corps solide ou liquide

La densité d’un corps solide ou liquide est le rapport de la masse d’un certain volume de ce corps à la masse d’un égal volume d’eau.

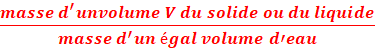
d==

ρ est la masse volumique du corps considéré et ρ’ est la masse volumique de l’eau.

La densité, rapport de deux grandeurs de même nature, n’a pas d’unité.

Densité d’un gaz.

La densité d’un corps C gazeux se définie par rapport à l’air : C’est le rapport de la masse d’un volume V du gaz sur la masse du même volume d’air. d = m_C/m_air

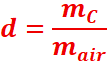
On montre que :

d =

d = m_C/m_air=mc/ρ_air or n=V_air /V_m =m_c/M=ρ_air.V_air => d=M/ρ_air.V_m=M/ 1,3x22,4=M/29

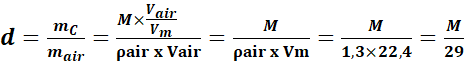
Car ρ_air=1,3kg/m³ (masse volumique de l’air)

Vm=22,4l.mol^-1(Volume molaire)

Remarque :

La densité n’a pas d’unité, on peut mesurer directement la densité d’un corps grâce à un densimètre.

Exercices d’application :

1. Déterminer la densité d’un litre de dioxygène de masse 1,43g sachant que la masse d’un litre d’air est de 1,29g.

- Déterminer la masse volumique d’une porte de masse 1,3kg, en forme de parallélépipède sachant que sa longueur est de 2m, sa largeur de 1m et son épaisseur de 2,5cm ?

- Quel serait sa masse si son volume est de 50cm³?

- Quel serait le volume d’une porte de 500g faite de la même matière ?

EXERCICES

EXERCICE I :

1. Un câble électrique cylindrique en cuivre de longueur l=90km. Le diamètre du fil D=1cm et la densité du cuivre est 8,9. Calculer sa masse.

2. Un câble électrique à haute tension en aluminium a 80 mm de diamètre. Calculer le poids d’un km de câble sachant que la masse volumique de l’aluminium est 2500 kg/m³ et que g=9,780N/kg.

3. Calculer la masse volumique de la terre sachant qu’elle est assimilable à une sphère de masse M=6.10²⁴ Kg et de diamètre D= 12800 Km.

EXERCICE II :

Le mercure est un métal qui, à la température ordinaire est liquide.

1. Calculer la masse du mercure contenue dans le tube cylindrique de diamètre intérieur d=1cm et de hauteur h=76 cm.

2. Comparer cette masse à celle d’un égal volume d’eau. En déduire la densité du mercure.

On donne la masse volumique du mercure : 13600Kg/m³

EXERCICE III :
Le laiton est un alliage de cuivre et de zinc. La masse volumique du zinc est 7,1kg/L, celle du cuivre 8,9kg/L.
1/ Sachant que le laiton renferme en masse 40% de zinc, déterminer les masses de zinc et de cuivre présents dans 1kg de laiton.
2/ On admettra que le volume du laiton est égal à la somme des volumes de cuivre et de zinc. Trouver la masse volumique du laiton.

EXERCICE IV :
A) Une règle parallélépipédique a pour dimensions 20cmx4cmx0,8cm. La masse volumique de la substance qui constitue la règle est 1,62 g/cm³. La masse de la règle est 72 g.
1- La règle est creuse, pourquoi ?
2- Quel est le volume de la partie creuse ?
3- Quel est le poids de cette règle à l’équateur ? On donne g=9,78 SI au sol à l’équateur.
B) En mélangeant 50 mL d’alcool (de masse volumique 794 Kg/L) et 50 mL d’eau, on obtient une solution de masse volumique 913 Kg/m³. Montrez que le mélange s’accompagne d’une contraction de volume que vous calculerez.
C) Un litre d’eau pure est congelé. Le volume de la glace est 1,095 dm³.
1- Trouvez la masse volumique et la densité de la glace.
2- Quel est le volume d’eau liquide ayant même masse que 10 cm³ de glace ?

RESOLUTION

EXERCICE I :

1.Volume du câble :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image004.png$

Masse volumique du cuivre :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image006.png$ $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image008.png$ $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image010.png$

Masse du câble :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image008.png$

2. Volume du câble au km :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image012.png$

Masse du câble :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image014.png$

Poids du câble : P=mg=12560x9,78=122836,8 N

3. Volume de la terre :

V= $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image016.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image018.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image020.png$ ³¹⁵

Masse volumique :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image022.png$ =

EXERCICE II :

1. Volume du mercure :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image026.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image028.png$

Masse du mercure :

m_mercure=ρV=13600x0,6.10^-4=0,816kg

2. Egal volume d’eau : m_eau =1000x0,6.10^-4=0,06 kg

Rapport :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image032.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image034.png$

EXERCICE III :

1.Masse du zinc : 40%masse laiton=0,4x1000=400g

Masse du cuivre =1000-400=600g

2. $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image040.png$ <= > $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image042.png$ $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image044.png$ = > $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image046.png$

EXERCICE IV :

A)1.Volume de la règle :

V=20x4x0,8=64cm3

Masse théorique :

m=ρV=1,62x64=87,48g

Masse réelle :

72g inférieure 87,48g donc la règle est creuse.

2. Volume de la partie creuse :

Volume théorique – Volume réelle

= $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image050.png$

3.Poids de la règle :

P=mg=72.10^-3 x9,78=0,704N

B)1. Masse du mélange attendu

: $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image052.png$ 794x0,05 +1000x0,05=89,7kg

Masse du mélange obtenu :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image054.png$ 913x0,1=91,3 kg

Différence de masse :

91,3-89,7=1,6 kg correspondant à un volume de $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image056.png$ =0,00175L

Le volume contracté est 0,1-0,00175=0,0982L

1.Masse volumique de la glace :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image058.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image060.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image062.png$ =913kg/m³

Densité de la glace :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image064.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image066.png$ =0,91

2. Masse de 10cm³ de glace :

$Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image068.png$ =913x10.10^-6=913.10^-5 kg

Masse d’un égal volume d’eau

= $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image070.png$ => $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image072.png$ => $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image072.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image074.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image076.png$ = $Description : C:\Users\FUJITSU\Documents\camexams\exercices2_phys_2nde_fichiers\image078.png$ =9,13cm³.