DERIVEES
DEFINITION
Soit f, une fonction numérique
définie sur I, un intervalle et x0 est un réel 
I. On dit que f est
dérivable sur I si :
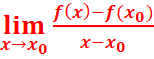existe et est finie.
Cette limite est appelée
le nombre dérivé de f en x0. On le note : f’(x0).
Exemple :
=
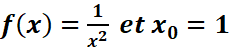
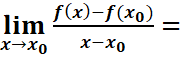
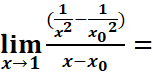
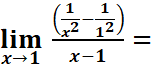
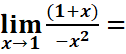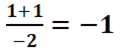. f est dérivable x0=1
=
=
= 
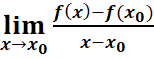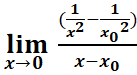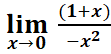= -∞. f n’est pas dérivable x0=0
CALCUL DES DÉRIVÉES
Soit f une fonction et f’ sa dérivée,
on a les tableaux suivants :
OPERATIONS SUR LES
FONCTIONS DERIVABLES
Soient f et 𝑔 deux fonctions dérivables sur un intervalle I de et k un
nombre réel non nul.
|
cosf |
-f’sinf |
|
sinf |
f’cosf |
Exemple :
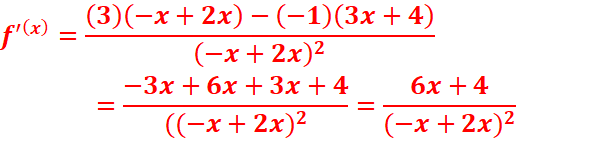
COMPOSITION DES FONCTIONS
DERIVEE SUCCESSIVE : POINT D'INFLEXION
. Lorsque la dérivée
seconde s'annule en un point d'abscisse x0 en changeant de signe,
alors
le point d'abscisse x0 est appelé « point d’inflexion ».
. Au point d'inflexion, la courbe
traverse la tangente et change de concavité
EQUATION DE LA TANGENTE A LA COURBE D’UNE.
FONCTION
·
Soient une
fonction f, (C) sa courbe représentative et A un point de (C) d’abscisse x0.
Si f est dérivable en x0, alors(C) admet en A une tangente (T) dont
le coefficient directeur est f’(x0).
La tangente (T) en x0 a
pour équation :
y=f’(x0)(x-x0)
+ f(x0)
Exemple :
f(x)=x2
+2 et x0=3
f’(x) =2x
f’(3=2(3)=6
f(3)=(3)2 +2 =11
L’équation
de la tangente en 3 est : y=6(x-3) + 11=6x+29=> y=6x +29
·
Si f’(x0) =0, alors (C) admet au point abscisse x0 une
tangente parallèle à l’axe des abscisses (horizontale) d’équation y =f(x0).
SENS DE VARIATION
RECHERCHE DES EXTREMA
Soient la fonction dérivable sur I,
un intervalle donné et Cf sa courbe représentative dans un repère
orthonormé (O,
)
On dit que (Cf) admet un extrémum
au point A(x0,f(x0)) si f’(x0)=0
et pendant l’étude du signe de la dérivée , on observe un changement de signe.
Si f croit et décroit ensuite, on a
un maximum en M0. Il correspond à la plus grande ordonnée. La courbe
admet une tangente horizontale en M0.
Si f décroit et croit ensuite, on a un
minimum. Il correspond à la plus petite ordonnée. La courbe admet une tangente
horizontale en M0.
TABLEAU DE VARIATION
EXERCICES
EXERCICE
I :
Déterminer les dérivées de :
i)
ii)
iii)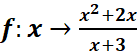
EXERCICE
II
Dans chacun des cas suivants, déterminer la dérivée de la
fonction f :
1. 
sin(x-x2)
2. 
3. 
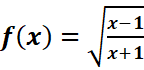
4.
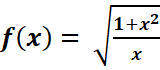
5.
6.
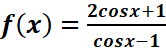
EXERCICE III :
On
considère la fonction rationnelle définie par :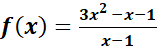 
. On désigne par
Cf sa représentation graphique.
1.
Déterminer une équation de la tangente (T) à Cf au point d’abscisse 0.
2.
Cf admet-elle une tangente de coefficient directeur à 0 ?
3.
Existe-t-il des points de Cf où la tangente est parallèle à la droite
d’équation 11x +4y-1=0 ?
CORRIGES
EXERCICE I :
i)
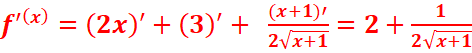
ii) 
=
=
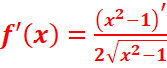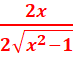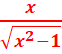
iii)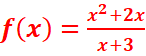
=
=
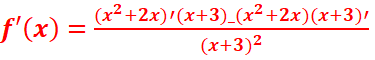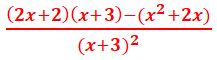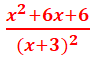
EXERCICE II :
Dans chacun des cas suivants,
déterminer la dérivée de la fonction f :
1. f(x)=sin(x-x2)
f’(x)=(x-x2)’cos (x-x2) = (1-2x) cos (x-x2)
2. 
=
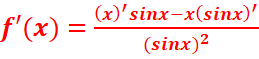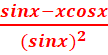
3. 
=
=
= 
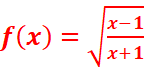
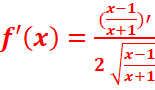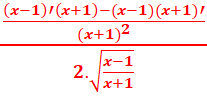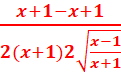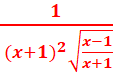
4.
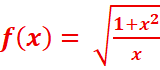
f’(x)=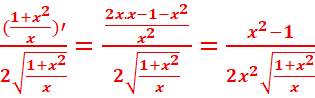
5.
f’(x)=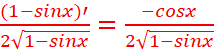
6.
= 
=
=
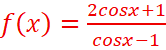
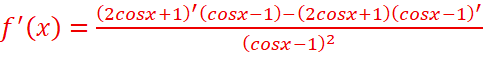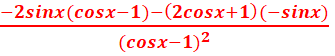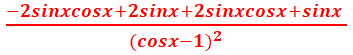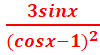
EXERCICE III :
1. Equation de la tangente (T) à Cf au point
d’abscisse 0.
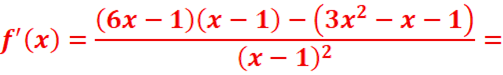
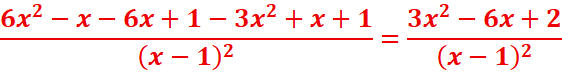
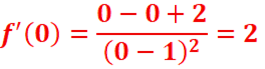
y=f’(x0)(x-x0)
+ f(x0)
y=f’(0)(x-0) + f(0)=2x+1
2. Tangentes de coefficient
directeur à 0
f’(x)=0 <= >
<= >
=>
f(
f(
Cf admet deux tangentes horizontales
aux extremum, parallèles à l’axe des x d’équations :
y=f’(x0)(x-x0)
+ f(x0)=0 +5-2Ѵ3=5-2Ѵ3
y=f’(x0)(x-x0)
+ f(x0)=0 +5+2Ѵ3=5+2Ѵ3
3. Points de Cf où la tangente
est parallèle à la droite d’équation 11x +4y-1=0
Soit x, l’abscisse de ce point,
on doit avoir f’(x)= -11/4 pour que la tangente à ce point soit parallèle à la
droite
11x +4y-1=0 (ou y= -11/4 x – 1/4)
=>
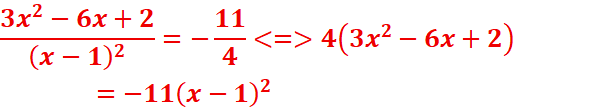
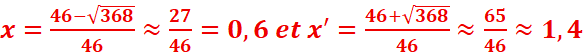
f(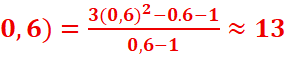
=> M(
f(
=>
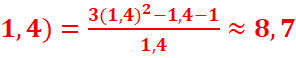N(
Avez-vous
un exercice à proposer ? Cliquez-ici
Merci de votre visite
Laissez un commentaire