RADIOACTIVITÉ
REACTIONS
NULEAIRES SPONTANNEES
Définition
La radioactivité est une propriété des noyaux
atomiques instables de se transformer spontanément en noyaux d’une autre espèce
avec une émission de particules accompagnée de rayonnement électromagnétique.
La radioactivité
naturelle est celle qui existe naturellement dans la nature. La radioactivité
artificielle est celle obtenue par bombardement des noyaux atomiques par des
particules (neutrons, protons, particules alpha, électrons, positrons,
..).
Les réactions
nucléaires sont des réactions des noyaux d’atomes. La radioactivité est donc
une réaction nucléaire car elle ne concerne que les noyaux des atomes et non
des électrons.
Les émissions radioactives se composent des
particules chargées électriquement (α, β-, β+) et d’un rayonnement
électromagnétique γ
-Les particules α sont des noyaux d’hélium 
-les particules β- sont des électrons que nous
noterons 
-les particules β+ sont des
antiparticules de l’électron appelés positons
ou positrons que nous noterons 
-le rayonnement γ est un
rayonnement électromagnétique de très courte longueur d’onde(10-4nm).
Très pénétrant, il est capable de traverser une plaque de plomb de 20 cm
d’épaisseur. C’est la partie de rayonnement la plus dangereuse biologiquement.
Détection des émissions radioactives
Pour détecter une
émission radioactive, on utilise les propriétés des rayonnements :
-Les compteurs à
scintillations utilisent la propriété qu’ont les rayonnements
d’exciter la fluorescence de certaines substances comme le sulfure de zinc.
-Le compteur de
Geiger-Muller utilise la propriété ionisante des rayonnements. Ce
compteur est composé d’un tube contentent un gaz raréfié.
Mécanisme de
de transformation radioactive
Lois de
conservation
Les réactions
nucléaires obéissent aux lois de conservations suivantes :
-La conservation du nombre de charge :la somme
des nombres de charge des noyaux disparus est égale à celles des noyaux formés
-La conservation du nombre de masse : la somme
des nombres de masse des noyaux disparus est égale à celle des noyaux formés.
-la conservation de l’énergie :au cours d’une
réaction nucléaire, la masse des noyaux consommes est différente de celle des
noyaux formés. L’équivalence énergie de cette différence de masse est l’énergie de désintégration.
A=A’ + a (conservation du
nombre de nucléons)
Z=Z’ + z
(conservation du nombre de protons)
Radioactivité α
La
radioactivité α est l’émission des noyaux d’hélium par certains noyaux.
Certains noyaux lourds (N+Z > 200) émettent des particules
alpha. Le noyau expulse une particule alpha. La transformation s’écrit :
Le nucléide X est appelé "noyau père", le
nucléide Y "noyau fils". X et Y correspondent à des éléments
chimiques différents.
Exemple : L’atome de polonium 210 se transforme, par désintégration α, en
plomb 206 :
Radioactivité β-
Lorsque les particules émises sont des électrons, on dit que le noyau
subit une désintégration β-
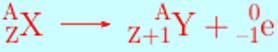
Exemple : L’atome de potassium 40 se transforme, par désintégration β−,
en calcium 40 :
Dans Les noyaux qui
donnent lieu à la radioactivité β-, les neutrons sont en excès. Un neutron
se transforme en un proton et un électron selon l’équation :
Remarque : Quelquefois, l’émission de l’électron s’accompagne de l’émission d’un antineutrino (particule de masse
nulle). L’antineutrino est une particule de charge nulle, de masse quasi-nulle,
se déplaçant à la vitesse de la lumière.
La réaction s’écrit :
L’équation bilan devient :
Exemple :
L’antineutrino
garantit la conservation de la quantité de mouvement et de l’énergie.
Radioactivité β+
Les particules émises par les noyaux sont des positons.
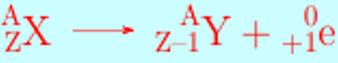
Exemple : Le fluor 18 se transforme, par désintégration
β+, en oxygène 18 :
Remarque : L’émission d’un positon s’interprète par la transformation d’un proton
en neutron :
Cependant l’émission
d’un positon peut être accompagnée de celle d’un neutrino, antiparticule de
l’antineutrino, notée :
La réaction s’écrit :
L’équation bilan devient :
Exemple :
Le neutrino garantit
la conservation de la quantité de mouvement et de l’énergie.
Remarque : pour des raisons de simplification, ces particules notées 
et 
ne figurent pas dans les équations
de désintégrations.
Radioactivité γ
Après une transformation radioactive du noyau, le noyau fils est souvent
dans un état excité (*) et se désexcite en émettant un (ou plusieurs) photons
de haute énergie (gamma). L’émission d’un rayonnement par un noyau ne
s’accompagne pas par un changement de la nature du noyau, mais elle correspond
plutôt à la perte d’une certaine quantité d’énergie.
Au même titre que les
atomes, les noyaux peuvent se trouver dans un état excité. La désexcitation
d’un noyau 
vers son état
fondamental 
s’accompagne
par émission gamma (γ),
Remarques :
• Toutes les désintégrations sont accompagnées d’une libération d’énergie.
• Il existe
d’autres types de radioactivité : émission de protons, neutrons, …
• Les
neutrinos et antineutrinos électroniques sont des particules de charge
électrique nulle, de masse au repos très petite, et n’interagissant que très
peu avec la matière.
Loi de la désintégration radioactive
La désintégration radioactive est un phénomène aléatoire qui aura lieu
avec une certaine probabilité. Lorsqu’un noyau se désintègre, il est transformé
en un autre nucléide, qui peut être radioactif ou non.
Si à
l’instant t = 0 on a N0 noyaux radioactifs, après un certain temps t
il reste N(t) < N0.
Soit dN le nombre de
noyaux qui se désintègrent dans un intervalle de temps dt.
On a : dN=-λNdt
λ est la constante de désintégration. Unité : s-1.
Elle représente la probabilité de désintégration par
seconde.
Le signe – indique que le nombre N de noyaux
diminue, donc dN < 0.
On a donc l’équation différentielle suivante :
N
Afin de résoudre cette
équation différentielle on intègre à gauche et à droite,
On obtient :
La courbe de
désintégration est :
Demi-vie T d'un radioélément
On appelle demi-vie T
(ou période radioactive) d’un radioélément le temps au bout duquel le nombre N , a diminué de moitié.
En t=T, on a N(T)=N0/2,
donc : 
Cette relation
fournit :
Suivant leur
stabilité, la demi-vie des noyaux radioactifs peut aller de quelques
millisecondes jusqu’à des milliards d’années. Elle est caractéristique pour
chaque nucléide.
Activité
d’une source radioactive
Définition
L’activité A d’une
source radioactive est le nombre de noyaux radioactifs qui se désintègrent par
seconde. C'est aussi le nombre de particules ou de photons émis par unité de
temps.
Si dans un intervalle
de temps dt, dN atomes se
sont désintégrés, l’activité vaut :
Unité : 1 becquerel=1 Bq= 1 s-1
A l’aide de la
loi de désintégration, on obtient :
A=λN et en posant A0=λN0 , on obtient :
A=A0e-λt
REACTIONS
NUCLEAIRE PROVOQUEES
Une réaction nucléaire
est provoquée lorsqu’un noyau projectile frappe un noyau cible et donne
naissance à deux nouveaux noyaux. Les réactions nucléaires de fusion et de
fission sont qualifiées de réactions provoquées : Elles doivent vérifier les lois de
conservation comme toutes réactions nucléaires :
- Conservation du
nombre de masse (ou nombre de nucléons)
-Conservation du
numéro atomique (ou nombre de protons)
La fission nucléaire
La fission nucléaire
est la rupture du noyau sous l’action d’un neutron de faible énergie
électrique.
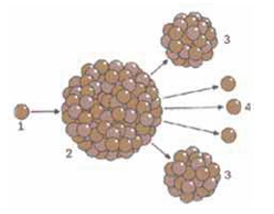
L’énergie libérée par
une réaction de fission est :
E=|Δm|c2=(mreactifs-mproduits).c2
La fission d’un atome
d’uranium 235 libère une énergie de l’ordre de 200 Mev.
Les neutrons émis peuvent à leur tour attaquer d’autres noyaux et provoquer une réaction de fission en chaine. Si cette réaction n’est pas contrôlée, il se produit une violente
explosion libérant d’énormes quantités d’énergie : c’est la bombe
atomique.
La fusion nucléaire
Dans une réaction de
fusion, deux nucléides légers fusionnent pour donner un nucléide lourd.
Pour avoir une fusion nucléaire, il faut que deux noyaux légers
s’unissent pour donner naissance à un noyau plus lourd. Ces noyaux légers sont
cette fois-ci composés de neutrons et de protons, ainsi, il leur faut une très
grande énergie pour vaincre les forces de répulsion : On porte alors le milieu
à très haute température (108 K). En conséquence, la réaction de fusion est
appelée réaction thermonucléaire.
La bombe a hydrogène ou bombe H est le
résultat d’une réaction de fusion thermonucléaire non contrôlée.
EXERCICES
EXERCICE
I :
Soit la réaction nucléaire suivante :
1.
Quelles sont les règles qui permettent de déterminer A et Z ?
Calculer ces valeurs, déterminer 
2.
Définir le défaut de masse Δm de la réaction.
3.
Calculer l’énergie libérée par 1 noyau d’uranium, puis pour un kilogramme si Δm=3,82464.10-28 kg
4.
La combustion d’une tonne de charbon libère 2,5.1010 J. Quelle masse
de charbon libère, en théorie, autant d’énergie qu’un kilogramme d’uranium ?
Données : M = 234 g/mol ; c = 299792458
m.s-1 ; NA = 6,02.1023 mol-1
EXERCICE
II :
Le
potassium 40 (
) est un atome radioactif présent dans la
nature. Le corps humain contient 4,2 mol de potassium, dont seulement 0,01167 %
est du potassium 40 radioactif.
1.
Quelle est la masse de potassium dans le corps humain ? Quelle est la masse de
potassium radioactif dans le corps humain ?
2.
Le potassium 40 se désintègre en subissant une désintégration β-. Ecrire
cette désintégration
3. L’activité d’un gramme de potassium 40 vaut
263.103 Bq. Que signifie cette donnée ?
4.
La période radioactive du potassium 40 vaut 1,248 milliards d’années. Que
signifie cette période ?
Données
:
M () = 40 g/mol (potassium
radioactif) ; M( 
) = 39 g/mol (potassium
radioactif et non radioactif).
EXERCICE
III:
Un laboratoire reçoit un échantillon de 1mg de
cadmium
de période T=6h42min. Il se désintègre en 
radioactif, de demi-vie avec émission d’une
particule chargée.
1.
Ecrire l’équation de désintégration sachant que la désintégration de cadmium
s’accompagne de l’émission d’un rayonnement.
De quel type de radioactivité s’agit-il ?
Expliquer le rayonnement émis.
2.
Définir la constante radioactive et calculer sa valeur.
3.
Calculer le nombre N0 de noyaux présents au moment de la réception
de l’échantillon
a) Donner l’expression de l’activité à la date
t d’un échantillon radioactif contenant N(t) noyaux.
b) Calculer l’activité de cet échantillon
étudié à la date t=0
c)
calculer la durée au bout de laquelle l’activité aura diminué des trois quarts
CORRIGES
EXERCICE I.
1.A et Z se conservent
A = 236-139-3 =94 et Z =
92-54-0=38 c’est donc : 
2. Le défaut de masse
représente la diminution de la masse des noyaux produits par rapport à la masse
des noyaux initiaux.
3. Si |∆m| = 3,82464.10-28 kg, El =|∆m|*c²=
3,4374.10-11 J pour un kilogramme N=n.NA =m/M.NA=4,273*6,02.1023
noyaux.
E = 8,836.1013 J
4. E/2,5.1010 =
3535 tonnes de charbon.
EXERCICE II :
1. Masse de potassium dans le corps m = nxM
= 4,2x39 = 163,8 g .
Masse du potassium
radioactif : n’=0,01167/100x4,2 = 4,9014.10-4 mol donc m’ = 4,9014.10-4x40 = 1,96.10-2 g de
potassium radioactif.
2. 
3. L’activité représente le
nombre de désintégration par seconde d’un gramme de potassium 40.
4. La période est la durée
au bout de laquelle le nombre de noyaux initialement présents se sont
désintégrés.
EXERCICE III :
1.𝐿’é𝑞𝑢𝑎𝑡𝑖𝑜𝑛 𝑔𝑙𝑜𝑏𝑎𝑙𝑒 𝑑𝑒 𝑙𝑎 𝑡𝑟𝑎𝑛𝑠𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛 𝑑𝑢 𝐶𝑎𝑑ni𝑢𝑚 𝑠’é𝑐𝑟𝑖𝑡 :
Conservation de A :107=107+A =>A=0
Conservation de Z :48=47+Z=>Z=+1
D’où :
L’argent Ag sous sa forme excitée, il doit se désexciter en émettant
des rayonnements gamma suivant l’équation :
2. Constante Radioactive : est une constante qui caractérise
l’élément radioactif, et a une dimension de l’inverse d’un temps.
=>
3) 
Bq
