NOYAU ATOMIQUE
LES
CONSTITUANTS DU NOYAU ATOMIQUE
Le noyau est constitué des protons
et des neutrons. On les appelle des nucléons.
Le proton est chargé d’électricité positive.
Charge du proton : qp=e=1,6.10-19C
Masse du proton : mp=1,67.10-27kg
Le neutron est électriquement neutre, il ne porte pas de charge
électrique.
Charge du neutron : qn=0
Masse du neutron : mn=1,67.10-27kg
Les protons sont les seuls
responsables de la charge positive du noyau.
Le nombre de charge, appelé numéro
atomique Z est égal au nombre de protons contenus dans le noyau.
Le nombre de masse A est égal au
nombre de nucléons (protons + neutrons) contenus dans le noyau.
Le nombre de neutrons N est
évidement égal à la différence entre A et Z : N=A-Z
Représentation d’un noyau
atomique ; 
Les
isotopes : Les atomes
qui ont le même numéro atomique Z, mais de nombre de masse A différents, sont
des isotopes de l’élément de numéro
atomique Z.
Exemple :
et
sont les isotopes de l’uranium
Nucléides : On appelle nucléide, une espèce
atomique caractérisée par le nombre de protons et de neutrons dans son noyau,
ainsi que par son état énergétique.
Ainsi, les isotopes sont des
nucléides qui ont le même nombre de protons (numéro atomique Z) mais un nombre
de neutrons différent.
ASPECT ENERGETIQUE DES NOYAUX
Défaut de masse
Le défaut de masse d’un noyau de
symbole 
est la différence entre la masse des nucléons isolés et au
repos et la masse du noyau au repos. On le symbolise par :
Les masses sont exprimées en unité
de masse atomique (symbole u).
1u =1,66054.10-27
Kg
Le défaut de masse est toujours
positif.
Equivalence Masse-Energie (Relation de d’Einstein)
Toute particule, même au repos, possède,
du simple fait de sa masse, une énergie E0 appelée énergie de masse
et dont la valeur est donnée par la relation :
E0=mc2
m en kilogramme (kg)
c en mètre par
seconde(ms-1)
E0 en joules(J)
Dans
cette relation, on prend :
c =3.108 m/s.
En
physique nucléaire, l'unité convenable de l'énergie est l’électronvolt et un de
ses multiples comme mégaélectronvolt MeV
Energie
équivalente à l'unité de masse atomique :
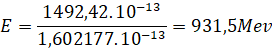
Energie de
liaison
L’énergie de liaison Eℓ
d’un noyau atomique est l'énergie qu'il faut fournir au noyau au repos pour le
dissocier en ses nucléons constitutifs pris au repos. (Eℓ est une
grandeur positive.).
Cette énergie est
positive.
Elle s’exprime en
mégaélectronvolt (MeV) :
Energie de
liaison par nucléon
L'énergie de liaison par nucléon est définie par la
relation :
E= Eℓ /
A
Son unité est le MeV/nucléon.
A partir de l’énergie
de liaison par nucléon, on peut comparer la stabilité de 2 noyaux radioactifs :
Plus l'énergie de liaison par nucléon est grande plus le noyau est stable.
EXERCICES
EXERCICE
I :
1.Calculer
en Mev l’énergie de liaison du noyau de Lithium 
.
On
donne :mp=1,0073 u ; mN=1,0087
u ; m(
)=7,0160 et u=1,66.10-27
kg.
2. Calculer, en Mev/nucléon, l’énergie de
liaison par nucléon du noyau du Lithium .
3. Calculer l’énergie libérée au cours de la transformation
ci-dessous :
On donne:
m(S) = 5,30763.10-26kg; m(P) = 5,30803.10-26kg;
m(e) = 9,1.10-31kg.
EXERCICE II :
On considère la réaction classique de fusion entre
un noyau de Deutérium et un noyau de tritium :
Déterminer l’énergie libérée au cours de cette
transformation.
CORRIGES :
EXERCICE I.
1.
El =Δm×
C2 avec Δm= 3 mP+4
mn - m(7Li)= 0,0407 u
et 1u=931,5 MeV/C2
E= 0,0407x
931,5 = 37,9 MeV
2. Eℓ
/A=37,9 /7=5,41 MeV
3.
Elibérée = |ΔE | avec ΔE =m×C2
Calculons Dm la variation de masse :
Δ m = mS+
me - mP
Δ m =
5,30763.10-26 + 9,1.10-31 - 5,30803.10-26 = -
3,09.10-30 kg.
ΔE =|Δm|×C2= 3,09.10 -30.(3.108)2=
2,781.10-13 J = 1,73 Mev
E libérée =
|ΔE|=- 1,73 Mev
EXERCICE II :
Calcul du défaut de masse
D'après
l'équation de cette réaction : Δm=m(neutron)+m(helium)−m(deutérium)−m(tritium)
Δm = (1,0087+4,0015−2,0160−3,0247).u
Δm=−0,0305u
Calcul de l'énergie correspondante :
E=∣Δm∣×c2
E=0,0305×1,660539.10−27×2997924582
J
E=4.55187497852.10−12 J
Mise en forme du résultat :
E=4.55187497852.10−12 J× 1Mev
1,602176.10−13 J
E=28,41 Mev