MISE EN EVIDENCE DE L’EFFET
PHOTOELCTRIQUE :
Expérience de HERTZ
Une plaque de zinc bien décapée est
placée sur le plateau d’un électroscope chargé négativement.
Observations :
-Lorsque la lame est éclairée par une
source de lumière riche en en rayonnements ultraviolets, les feuilles de
l’électroscope se rapprochent progressivement : l’électroscope se décharge.
-Lorsqu’on interpose sur le trajet
lumineux une lame de verre capable d’arrêter les rayons ultraviolets,
l’écartement des feuilles reste inchangé : l’électroscope ne se décharge plus.
-De même, lorsque la plaque est éclairée
par une lampe à incandescence, l’électroscope ne se décharge plus, quel que
soit la puissance de la lampe.
Interprétation :
La
décharge de l’électroscope s’interprète par le fait que les radiations
ultraviolettes ont expulsé les électrons libres du métal zinc. L’excédent
d’électrons de l’électroscope migre progressivement vers la lame de zinc.
L’autre observation montre que l’émission d’électrons par le métal zinc n’est
pas observée pour n’importe quel rayonnement de longueur d’onde donnée.
Définition de l’effet photoélectrique :
On
appelle effet photoélectrique, l’émission d’électrons par un métal
convenablement éclairé.
ETUDE EXPERIMENTALE DE L’EFFET PHOTOELECTRIQUE
Dispositif
expérimental :la cellule photoélectrique
Une cellule photoélectrique est
constituée de deux électrodes :
- la cathode C, cylindrique, est faite du
métal dont on veut extraire les électrons ;
- l’anode A, filiforme, est très souvent
en platine. L’ensemble est enfermé dans une enveloppe de quartz ou de verre
(transparents aux ultraviolets) dans laquelle on a fait un vide très poussé.
Pour étudier le courant photoélectrique, la cellule est insérée dans un
circuit électrique comprenant :
-Un générateur réglable qui établit une
tension entre les deux électrodes. Ceci crée un champ électrostatique dont les
lignes de champ sont radiales (le long des rayons du cylindre).
- Un voltmètre qui mesure la tension
appliquée à la cellule. En effet lorsque la lumière frappe la cathode, elle
fournit de l’énergie aux électrons qui quittent la cathode et se dirigent vers
l’anode.
- un galvanomètre (ampèremètre sensible
aux très faibles intensités) permettant de lire l’intensité du courant
photoélectrique.
La cellule est éclairée par une source de lumière monochromatique dont
on peut faire varier la puissance.
Observations : lois de de
l’effet photoélectrique
En
faisant varier la fréquence 
de la lumière incidente, on constate que
l’émission des électrons n’est possible que si la fréquence de la lumière utilisée est supérieure ou égale
à une fréquence
caractéristique
du métal.
A cette valeur limite de correspond une valeur limite λ0
de la longueur d’onde.
Les conditions du seuil photoélectriques
sont :
La fréquence de seuil d’un
métal est la fréquence minimale du rayonnement capable de provoquer l’émission
des électrons du métal.
La longueur d’onde de seuil λ0 est
la longueur d’onde maximale du rayonnement produisant l’effet
photoélectrique.
Pour 
, on constate que l’émission des
électrons commence et cesse avec l’éclairement :
l’effet photoélectrique est instantané. C’est la première loi de l’effet
photoélectrique.
CARACTERISTIQUE TENSION-COURANT
Pour
une radiation convenable, la mesure de l’intensité
i du courant photoélectrique en fonction de UAC, permet de tracer la
caractéristique tension-courant de la cellule photoélectrique :
-l’intensité i du courant photoélectrique
augmente avec la tension UAC : pour des valeurs élevées de la
tension accélératrice, elle atteint une valeur maximale I0 appelée intensité
de saturation :
Is=nse
-le courant photoélectrique s’annule à
partir d’une valeur négative de la tension -U0 appelée tension
d’arrêt.
La valeur absolue U0 de la
tension d’arrêt est le potentiel d’arrêt.
Ø Pour
deux radiations lumineuses de même fréquence et de puissance P1 et P2
différentes, l’intensité de courant de saturation augmente avec la puissance
mais la tension d’arrêt reste inchangée.
Le nombre ne d’électrons
extraits par seconde de la cellule est donc proportionnelle à la puissance
lumineuse :
C’est
la deuxième loi de l’effet photoélectrique.
Ø Pour
deux radiations de même puissance et de fréquence différentes produisant
l’effet photoélectrique, la fréquence lumineuse a une influence sur le
potentiel d’arrêt mais n’agit pas sur l’intensité du courant de saturation.
INTERPRETATION D’EINSTEIN DE
L’EFFET PHOTOELECTRIQUE :
Pour
interpréter l’effet photoélectrique, ALBERT EINSTEIN considère que :
·
La lumière est constituée de particules
de charge et de masse nulle appelées photons se propageant à la vitesse
de la lumière.
·
Chaque photon transporte une énergie
propre ou quantum d’énergie de valeur :
E = hυ
υ
est la fréquence du rayonnement
h=6,62.10-34J/s une
constante appelée constante de Planck.
·
C’est cette énergie transportée par un
photon qui sert à extraire l’électron de l’attraction du noyau puis, a lui
communiqué une énergie cinétique.
REMARQUE
: Si la fréquence υ du photon est supérieure à la fréquence seuil υ0,
l’énergie (E) du photon est supérieure à l’énergie d’extraction W0 ;
l’excédent d’énergie est communiqué à l’électron sous forme d’énergie cinétique
(Ec).
Le
bilan énergétique s’écrit alors :
A partir d’une valeur -U0
, plus aucun électron
n’atteint l’anode. L’énergie cinétique maximale des photoélectrons expulsés de la
cathode et atteignant l’anode avec une vitesse nulle peut être obtenue en
appliquant le théorème de l’énergie cinétique entre la cathode et
l’anode :
Ec(A)-Ec(C)= W(Fel), W(Fel) étant le travail de
la force électrique.
Car le travail de la force électrique et
résistant.
Si Ec<eU0,
plus aucun électron de parvient à l’anode car son énergie cinétique est
insuffisante : l’intensité du courant traversant le circuit et nulle.
Pour
une tension anode-cathode UAC :
DUALITE ONDE-CORPUSCULE
La lumière se présente sous deux aspects
:
-Un aspect ondulatoire : où elle est considérée
comme un phénomène vibratoire se propageant par une onde.
-Un aspect corpusculaire : où elle est
formée de corpuscules appelés photons qui sont animés d’une vitesse c (célérité
de la lumière) et transportant un quantum d’énergie E tel que E = hυ.
APPLICATIONS :
-
L’effet photoélectrique se retrouve dans les dispositifs de commande tels que :
la mise en marche d’un escalier roulant, l’ouverture automatique d’une porte,
le déclenchement d’un système d’alarme… « Un faisceau lumineux (invisible)
tombant sur une photopile y produit un courant photoélectrique dont la
suppression par un corps déclenche le fonctionnement d’un dispositif »
-
Il est aussi utilisé dans les cellules photovoltaïques par une transformation
de l’énergie solaire en énergie électrique.
EXERCICES
EXERCICE
I :
1.Qu’est-ce
que l’effet photoélectrique ?
-En
donner un exemple dans la vie courante.
-Calculer
l’énergie d’un photon de longueur d’onde 0,5µm (1µm=10-6m)
2-Une lumière de fréquence 𝜐=8,33.1014
Hz frappe une surface recouverte d’un matériau photoémetteur de fréquence seuil
photoélectrique 𝜐0=6,82.1014 Hz.
2.1-Exprimer,
puis calculer l’énergie transportée par un des photons de cette lumière ?
2.2-Cette
lumière provoque-t-elle l’effet photoélectrique dans le matériau recouvrant la
surface ? Justifier votre réponse.
On
donne : Célérité de la lumière dans le vide : 3.108m/s ;
Constante de Planck : 6,63.10-34 J.s
EXERCICE
II :
Un métal de longueur d’onde seuil
λ0=350 nm est successivement éclairé par des radiations
lumineuses de longueurs d’ondes λ1 = 200 nm ; λ2=
480 nm et λ3= 800 nm
1°)
Calculer en électronvolt le travail d’attraction de l’électron de ce métal.
2°)
En justifiant, donner la ou les longueurs d’onde(s) capable (s) de provoquer
(s) l’effet photoélectrique pour ce métal.
En
déduire l’énergie maximale des électrons en électronvolt.
Données : c = 3.108m/s
et h=6,62.10-34 J/s
EXERCICE III
On dispose de 3 cellules photoémissives. Les cathodes sont respectivement
recouvertes de césium (Cs) ; potassium(K) ; lithium (Li).
Les énergies d’extraction Wo d’un électron de ces
métaux sont données dans le tableau ci-dessous :
|
Métal |
Cs |
K |
Li |
|
Wo(eV) |
1.87 |
2.26 |
2.39 |
1-Qu’appelle-t-on énergie d’extraction ?
2-On éclaire successivement chaque cellule par une radiation
monochromatique de longueur d’onde l=0.59mm.
a-Calculer, en eV, l’énergie transportée par un photon.
-Avec laquelle de ces 3 cellules obtient-on l’effet photoélectrique ?
Justifier votre réponse.
c-Calculer, en joules l’énergie cinétique maximale des électrons
à la sortie de la cathode.
Qu’appelle-t-on potentiel d’arrêt ? Calculer sa valeur absolue
dans le cas où l’effet photoélectrique se produit.
EXERCICE IV
Situation problème
:
Le laboratoire
du collège « EN DO » a reçu un laser (source monochromatique) d’un bienfaiteur.
Monsieur BELA, enseignant responsable du laboratoire constate que la plaque
signalétique de cet outil est illisible. Cependant sur la liste des lasers
offerts par ce donateur à divers établissements, les longueurs d'onde sont
indiquées (voir informations). Afin d'identifier l'appareil reçu, ses élèves
ont été répartis en deux groupes.
Expérience réalisée par le premier groupe
La radiation émise par cette source est envoyée sur un atome d'hydrogène dans
son état fondamental, on constate que son électron passe au niveau 2.
Expérience
réalisée par le deuxième groupe
La radiation
émise par le laser éclaire une cellule photoélectrique dont la cathode est en
or. Un dispositif approprié montre que la vitesse maximale des électrons émis
est : Vmax=1,34×106m.s−1.
Informations :
Niveaux d'énergie de l'atome d'hydrogène : En=−13,6n2 (eV);
Travaux d’extraction de certains métaux :
|
Métal |
Sodium |
Argent |
Or |
|
Travail d'extraction (eV) |
2,7 |
4,3 |
5,1 |
Liste des
lasers offerts par le donateur
|
Laser |
L1 |
L2 |
L3 |
|
Longueur d’onde (μm) |
0,92 |
0,12 |
0,64 |
Données
: h=6,62×10−34J.s ; c=3×108m.s−1 ;
masse de l'électron : m=9,1×10−31kg; 1eV=1,6×10−19J
1- En
exploitant les informations obtenues par le premier groupe d'élèves et à l'aide
d’une démarche scientifique, identifie le laser reçu.
2- En exploitant les informations obtenues par le deuxième groupe d'élèves,
examine si ces deux expériences sont en accord. (BACCALAUREAT D 2025)
CORRIGES :
EXERCICE I :
1-C’est l’extraction d’électrons d’un métal convenablement éclairé.
- L’effet photoélectrique se retrouve dans les
dispositifs de commande tels que : la mise en marche d’un escalier roulant,
l’ouverture automatique d’une porte, le déclenchement d’un système d’alarme… «
Un faisceau lumineux (invisible) tombant sur une photopile y produit un courant
photoélectrique dont la suppression par un corps déclenche le fonctionnement
d’un dispositif »
- Il est aussi
utilisé dans les cellules photovoltaïques par une transformation de l’énergie
solaire en énergie électrique.
W=h 
2.1-W=h𝜐=6,63x10-34x8,33x1014=55,22.10-20=5,5
eV
2.2-W0=h𝜐0=6,63x10-34x6,82x1014=4,5
eV
W>W0 il y a effet photoélectrique
EXERCICE II :
1-W0=h𝜐0=hc/λ0=6,62.10-34/350.10-9=3,5
eV
2-
λ1=200nm<λ0 donc la première radiation est capable
de produire l’effet photoélectrique pour ce métal.
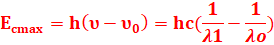
λ2=480nm>λ0
donc la première radiation est incapable de produire l’effet photoélectrique
pour ce métal.
λ3=800nm>λ0
donc la première radiation est incapable de produire l’effet photoélectrique
pour ce métal.
1-C’est l’énergie minimale nécessaire pour expulser un électron du métal.
2-Celle-ci est donnée par la relation E=h𝜐
b-On obtient l’effet photoélectrique
avec la cellule en césium car son énergie d’extraction est inférieure à
l’énergie transportée par le photon.
Wo(Cs)= 1,87eV < E =2,1eV.
c- E(photon)=Wo+Ec
Ec=2,1-1,87=0.23eV=0.23.1,6.10-19 J.eV-1=0,368.10-19J
d-Le potentiel d’arrêt U0 est le
potentiel qu’il faut donner à l’anode pour stopper le flux d’électrons,
donc annuler le courant.
Les électrons étant chargés négativement, ce potentiel U0 doit
être également négatif pour les repousser (ou plus exactement plus faible que
le potentiel de C ce qui revient à dire que la tension UAC entre
C et A doit être négative)
L’application du théorème de l’énergie cinétique permet d’évaluer
U0.
Etat initial= électron expulsé de la cathode avec une énergie cinétique Ec.
Le potentiel de la cathode est choisi nul.
Etat final=électron arrivant à l’anode avec une énergie cinétique nulle.
0-Ec=W(F)=qE.=-e.UCA(*)=-e(Vc-VA)=-e(0-VA)=VA
VA*e=-Ec
Effectuons le calcul en unité SI.(énergie en
joules)
VA=Uo=-Ec/e=-0.23*1.6.10-19/1,6.10-19=-0.23V.
Sa valeur absolue est donc :0.23V