LA
LOUPE
Définition
Une loupe
est une lentille convergente de petite distance focale. (En plaçant l’objet
entre la loupe et son plan focal objet, on obtient une image virtuelle droite
agrandie).
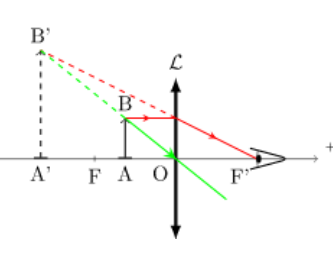 schéma 1
schéma 1
La mise au point
B’1∞
Mettre
au point, c’est ramener l’image entre les deux punctums de l’œil en modifiant
la distance de l’objet à la loupe.

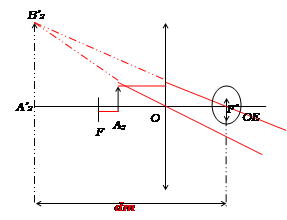
schéma 2
schéma 3
On appelle latitude de mise au point, la
distance FA2 des positions extrêmes entre lesquelles doit se trouver
l’objet pour que l’image soit visible.
La puissance
d’une Loupe
On appelle puissance
d’une loupe le quotient du diamètre apparent de l’image par la longueur de
l’objet.
P = ![]()
![]() : angle en rad
: angle en rad
AB : en mètre
P : en
dioptries
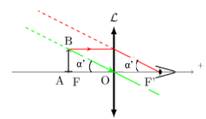
F’
Si la mise au point est réalisée pour
l’infini ou si l’œil est au foyer image, la puissance de la loupe est égale à
sa vergence. On l’appelle puissance intrinsèque.
Pi
= ![]()
Grossissement
Définition
On
appelle grossissement d’une loupe le rapport du diamètre apparent de l’image 𝜶’
au diamètre apparent de l’objet 𝜶 observé à l’œil nu à
la distance minimale de vision distincte.
G = ![]()
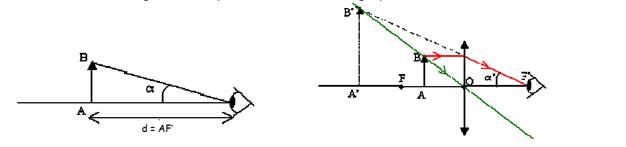
La relation entre
le grossissement et la puissance.
F
Le
grossissement d’une loupe est numériquement égal au produit de sa puissance par
la distance minimale de vision distincte de l’œil qui l’utilise.
G = P.dm
Le
grossissement commercial
Le grossissement
commercial, est calculé pour un œil observant à l’infini et dont la distance
minimale de vision distincte est dm = 0,25m
La puissance a alors la valeur
intrinsèque :
![]() et lié au grossissement commercial par la
relation :
et lié au grossissement commercial par la
relation :
|
Gc = Pidm = Pi x 25=25/f ou |
Gc = 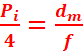
Le pouvoir
séparateur de l’ensemble œil-loupe
Supposons que M et N
soient deux points dont les images M’ et N’ sont tout juste séparée par l’œil
qui observe à travers la loupe.
La longueur MN
représente la plus petite distance de deux points objets vus et séparés à
travers la loupe.
MN = ![]()
ε : limite de séparation de l’œil en
rd
P: Puissance en dioptries
MN: en mètre
EXERCICES
EXERCICE I :
Une loupe a une distance focale f = 5 cm. Un objet
est placé à 4 cm de la loupe.
1. Où se forme l’image ?
2. Calcule le grandissement.
3. Sachant que l’œil est placé au foyer image,
calcule le grossissement G.
EXERCICE II :
1.Une loupe a une distance focale de 10 cm.
Où doit-on placer un objet pour que l’image soit à
la distance minimale de vision distincte (dm = 25 cm) ?
2.Une loupe de distance focale f = 4 cm est utilisée
de façon à obtenir une image à l’infini.
a-À quelle distance doit-on placer l’objet ?
b- Quel est alors le grossissement commercial?
EXERCICE III :
Calculer la distance de
l’objet à la loupe dans les positions extrêmes FA2 (latitude de mise
au point). L’objet est placé entre le plan focal objet et la loupe. L’œil est
placé en F’.
(Schéma 3)
La distance dm= 15 cm, la distance focale
f= 4cm.
EXERCICE
IV :
Une loupe d’horloge a 5 cm de distance focale.
Elle est utilisée pour un œil normal placé au foyer principal image pour
observer les détails d’un objet. Calculer la latitude de mise au point, sachant
que la distance minimale de vision distincte de l’œil est de 25 cm.
EXERCICE V :
Les
limites de vision distincte d’un myope sont situées entre 10 cm et 80 cm. Ce
myope utilise une loupe de 3 cm de distance focale, son œil étant placé au
foyer principal image.
a)
Calculer
la latitude de mise au point
b)
Que
devient cette latitude de mise au point si le myope porte des verres
correcteurs qui lui permettent de voir à l’infini.
CORRIGES :
EXERCICE
I :
1. Objet entre F et O → Image
virtuelle, droite, agrandie.
2. Grandissement γ = A'B'/AB =
-OA'/OA
Ici, OA = -4 cm ;
![]()

⇒ OA' ≈ -20 cm

⇒ image 5 fois plus grande.
3. Calcul du grossissement
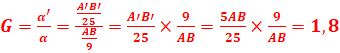
//grossissement commercial G = 25/f = 25/5 = 5
EXERCICE
II :
1-Image à 25 cm → OA' =
dm-f=25-10=15cm
![]()
![]() =>
=>
OA ≈ 6,57 cm → il faut
placer l’objet à 6,57 cm de la loupe.
2-a)Pour image à l’infini → objet au foyer
objet
![]()
![]() =>
=>![]()
Donc OA = -f = -4 cm
b-Calcul du grossissement commercial
G = 25/f =
25/4 = 6,25
EXERCICE III :
1- dm= 15 cm,
distance focale f= 4cm
B’2


![]() = dm - f
= dm - f
F’![]()
![]()
=
15 – 4 = 11 cm
A2 F PP A’2 O
![]()
![]()
![]()
dm
- ![]() +
+ ![]() =
=
![]() ] -
] - ![]() =
= ![]() -
-![]() =
= ![]()
![]() =
= ![]() ]
] ![]() =
= ![]()
AN:![]() =
= ![]() =
= ![]() =
= ![]() = -2, 93 cm
= -2, 93 cm
![]() = f -
= f -![]() = 4 – 2,93 = 1,07 cm
= 4 – 2,93 = 1,07 cm
EXERCICE
IV :
λ = ![]() =
= ![]() = 1 cm
= 1 cm
EXERCICE
V :
OA’ = 80 – 3
= 77 cm
OA’’ = 10 – 3 = 7 cm
a)
Pour voir au PR, il faut que l’objet soit placé à un point A1
tel que
- ![]() +
+ ![]() =
= ![]() ]
] ![]() =-
=- ![]() =
= ![]()
= 2,8875
Pour voir au
PP, il faut que l’objet soit placé à un point A2 tel que :
![]() =-
=- ![]() =
= ![]() = -2,1
= -2,1
d = ![]() -
- ![]() = -2,8875 + 2,1 = 0,7875 cm
= -2,8875 + 2,1 = 0,7875 cm
b)
PR = 6 ] ![]() = 3 cm
= 3 cm
d = 3-2,1 =
0,9 cm