INTERFERENCES LUMINEUSES
EXPERIENCE
DES FENTES DE YOUNG
Dispositif expérimental
Une source de lumière monochromatique issue de
S, sous l’effet de la diffraction, éclaire deux fentes S1 et S2
d’une plaque opaque. La diffraction de la lumière au niveau de ces deux fentes
donne deux faisceaux cohérents qui se superposent sur l’écran E. Une lumière
monochromatique ne contient qu’une seule radiation de longueur d’onde l
bien définie.

Observations :
Dans la zone de l’écran éclairée simultanément
par les deux entes S1 et S2, on observe un ensemble de
bandes brillantes, rectilignes et parallèles, alternant avec les bandes
sombres : ce sont des franges d’interférences.
Interprétation
L’étude
des interférences mécaniques a montré que la superposition de deux ondes
mécaniques issues de deux sources synchrones en mouvement rectiligne sinusoïdal
et de même amplitude produit des crêtes et des creux de forme hyperbolique
appelées franges d’interférences. L’observation des franges
d’interférences lumineuses résultant de la superposition de deux sources de
lumières identiques et monochromatiques conduit à penser, par analogie, que la
lumière se comporte comme une onde. Par conséquent, l’interférence lumineuse
constitue ainsi une preuve de la nature (phénomène, caractère ou modèle)
ondulatoire de la lumière.

Suivons
deux rayons lumineux issus de la source et parcourant deux chemins distincts
avant de se rejoindre en un point M du champ d’interférence.
d1=S1M et d2=S2M
La différence des trajets lumineux S1M
et S2M est appelée différence de marche notée :
![]()

L’existence des franges s’explique de la
manière analogue à celles observées à la surface de l’eau.
-En
un point d’une frange brillante, se superposent deux ondes provenant de S1
et S2 et arrivant en phase (interférence
constructive).
Les
points d’une frange brillante vibrent avec une amplitude maximale.
![]() avec k ϵ Z
avec k ϵ Z
-En
un point d’une frange sombre, se superposent deux ondes provenant de S1
et S2 et arrivant en opposition de phase (interférence
destructive).
Les
points d’une frange sombre vibrent avec une amplitude nulle.
![]() avec k ϵ Z
avec k ϵ Z
Position des franges
Considérons
les triangles rectangles S1IM et S2JM :
S1IM
est rectangle en I :
![]()
S2JM
est rectangle en J :
![]()
On
alors :

Les positions des
franges, mesurées à partir de l’origine O, sont respectivement :
Ø Pour les franges
brillantes
 avec k ϵ Z
avec k ϵ Z
Ø Pour les franges
sombres
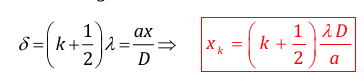 avec k ϵ Z
avec k ϵ Z
L’interfrange
Pour les franges brillantes : ![]()
Pour les franges sombres : ![]()
![]()
Ordre d’interférence
Les
positions des franges brillantes sont données, en fonction de l’interfrange
par :![]()
Celles
des franges sombres par : ![]()
On appelle ordre
d’interférence le rapport ![]()
Si ![]()
Si ![]()
Intensité lumineuse
Les ondes associées à chaque rayon lumineux
peuvent être représentées par des fonctions sinusoidales : s1=s2=s0costωt.
soit φ le déphasage en un point M du champ d’interférence entre les ondes
issues des sources S1 et S2, on montre que l’intensité
lumineuse en un point est proportionnelle au carré de l’amplitude de l’onde
résultante en ce point :
![]()
Avec
la géométrie du dispositif utilisé :
![]()
L’intensité
lumineuse est une fonction sinusoïdale des espaces de la période spatiale égale
à l’interfrange i.
INTERFERENCES EN LUMIERE BLANCHE
La
dispersion de la lumière blanche par un prisme montre qu’elle est le résultat
de la superposition de plusieurs couleurs. C’est une lumière polychromatique.
Une lumière polychromatique est constituée d’un grand nombre de radiations de
longueurs d’onde différentes.
On remplace la lumière monochromatique par une
lumière blanche dans l’expérience de Young.
Observations
-
Au centre une frange brillante blanche ;
-
De part et d’autre de la frange centrale, des franges brillantes irisées
(couleur de l’arc-en-ciel)
-Plus
loin, une coloration blanchâtre appelée blanc d’ordre supérieur.
Interprétation :
Au centre O de l’écran, la différence de marche
est nulle pour toutes les radiations. La superposition des franges brillantes
de différentes couleurs donne une frange centrale blanche.
Lorsqu’on s’écarte de O, les systèmes de
franges ne coïncident plus car l’interfrange i dépend de λ. A une distance
plus grande de la frange centrale, l’œil ne voit que du blanc grisâtre appelé
blanc d’ordre supérieur. Lorsqu’on l’analyse au spectroscope, on voit des
bandes noires correspondant aux radiations manquantes (qui présentent une
frange obscure). Le spectre est dit cannelé.
SPECTRE ELECTROMAGNETIQUE DE LA LUMIERE

EXERCICES
EXERCICE I :
Le dispositif comprend
une plaque percée de deux trous de Young distants de a =500 µ m. En utilisant
comme source émettrice S un laser He-Ne, de longueur d’onde λ= 633 nm on
produit des interférences sur un écran. La plaque est placée à une distance d
=20 cm de la source, l’écran à une distance D = 4 m de la plaque. Les deux
trous de même diamètre sont placés à égale distance de la source et se
comportent comme deux sources synchrones et cohérentes.

1.
Expliquer le phénomène d’interférences en quelques lignes.
2. Au point O, la
frange est-elle brillante ou sombre ? Justifier.
3. Etablir la formule
donnant l’interfrange
4. Donner la valeur de l’interfrange i
obtenue avec le laser He-Ne.
On réalise une expérience d’interférences lumineuses à
l’aide du dispositif des fentes d’Young. Les deux fentes F1 et
F2 sont distantes de a=0.4mm et sont éclairées par une fente
source de lumière monochromatique parallèle et équidistante de F1 et
F2. L’écran d’observation est disposé parallèlement au plan des
fentes F1 et F2. La distance qui sépare le plan des
fentes à l’écran est D=1m.
La longueur d’onde dans le vide de la lumière utilisée
est : λ=0.54mm.
1-Expliquer brièvement ce qu’est une lumière monochromatique.
2-Faire le schéma du dispositif. Précisez la marche des rayons lumineux.
Indiquez sur le schéma le champ d’interférence.
3-a/Décrire le phénomène observé sur l’écran.
b/calculer l’abscisse x=OM du point M de l’écran sur
lequel passe la 4éme frange brillante du système. On notera « 0 » la
frange centrale du système.
4-On remplace la radiation de longueur d’onde λ par une autre
radiation de longueur d’onde λ’
a/ sachant que la position de la 4éme frange obscure du
système est x’=5.4mm, calculer la valeur de λ’.
b/calculer la position de la 4éme frange brillante du
nouveau système.
EXERCICE III :
Deux
sources lumineuses ponctuelles S1 et S2 constituent des
sources secondaires monochromatiques d’un dispositif interférentiel de Young de
source principale S. L’écran E est orthogonal à la médiatrice de S1S2 ;
leur point d’intersection est O.
1 Qu’observe-t-on sur
l’écran ?
2 Etablir l’expression
de la différence de marche en un point M voisin de O, des vibrations issues de
S1 et S2, en fonction de a, x, D.
AN : a = 1,00
mm ; x = 10,0 cm ; D = 2,000m
3 Calculer
l’interfrange pour la longueur d’onde dans le visible λ.
AN : λ =
650nm.
4 On place devant la source S1, une lame à face parallèle
d’épaisseur e, d’indice n. Démontrer dans quel sens et de combien se déplace la
frange centrale ?
AN : e =
100μm n = 1,51.
5° S se trouve à la
distance d = 10 cm de I . On déplace la fente source S
suivant l’axe vertical yy’ vers le bas d’une distance
y= 3,5.10-3m.
5.1 Déterminer la
différence de chemin optique du point M.
5.2 calculer le déplacement de la frange
centrale
EXERCICE
IV :
Le
dispositif interférentiel de Young représenté ci-contre permet d’obtenir deux
sources lumineuses ponctuelles S1 et S2 synchrones et
cohérentes par dédoublement d’une source unique S placée en O. Les deux sources
S1 et S2 sont distantes de a = 1mm. Le plan (P) de
l’écran d’observation, parallèle à S1S2 est situé à la
distance D=IO = 2 m du milieu de S1S2.

La
source S émet une radiation monochromatique de longueur d’onde λ.
1.
Quelle est la direction des franges observées a
l’écran ? Pourquoi sont-elles dites délocalisées ?
2.La
distance comprise entre la troisième frange brillante et la cinquième frange
brillante situées de part et d’autre de la frange centrale est d=6,4 mm
Quelle
est la longueur d’onde λ de la lumière émise par la source
monochromatique ?
3.
On place derrière la fente S1 une lame de verre de très faible épaisseur e=4,8
μm et d’indice absolu n=1,5. Dans quel sens et de combien se déplace la
frange centrale ?
Quel
est alors l’ordre de la range qui a pris sa place en O.
4.La
source S est à présent éclairée par une lumière composée de deux radiations
monochromatiques de longueur d’ondes respectives λ1=0,42 μm et
λ2=0,60μm
4.1-Qu’observe-tt-on
sur l’écran ?
4.2-
a quelle distance du point O observe-t-on sur l’écran la première coïncidence
entre deux franges brillantes correspondant aux deux systèmes de franges ?
EXERCICE V :
On considère le
dispositif des fentes d’Young constitué de deux fentes très fines S1 et S2
horizontales et séparées par une distance a = 1 mm, d'un écran (E) parallèle au
plan (P) contenant S1 et S2 et d’une source de lumière monochromatique S.
L’écran (E) est à une distance D = 2 m du milieu I de [S1S2]. La source
lumineuse S est sur la médiatrice de [S1S2]. Cette médiatrice coupe l’écran (E)
en un point O. La longueur d’onde dans l’air de la lumière monochromatique est l = 650 nm.

1.Une
figure se forme sur (E). Indiquer le nom du phénomène correspondant.
2.Citer, en les
expliquant, les conditions remplies par S1 et S2 pour l’obtention de cette
figure.
3. On considère un
point M de la figure obtenue sur l'écran (E) tel que .
Soient d1 = S1M et d2 = S2M. Ecrire la relation donnant la différence de marche
d = d2 – d1 en fonction de
a, D et x. OM=
4 Donner la définition
de l’interfrange i.
5.Donner l’expression
de i en fonction de l, D et a puis
calculer sa valeur.
6. Le point O coïncide
avec le centre d’une frange appelée frange centrale.
6-1) Calculer la
différence de marche d correspondant à O.
6-2) Préciser si cette
frange est brillante ou sombre. X
7. Soit N le centre
d’une frange correspondant à d = 2,275 mm.
Préciser si cette frange est brillante ou sombre.
8. S
se trouve à la distance d = 10 cm de I. On déplace S verticalement de y = 1 cm
du côté de S1.La nouvelle différence de marche s’écrit
:
![]()
Dire dans quel sens se déplace le centre de la
frange centrale (du côté de S1 ou du côté de S2) et calculer le déplacement.
EXERCICE VI:
On observe l’expérience de Young à l’aide
d’une fente F équidistante de deux autres fentes F1 et F2, parallèles percées
dans un écran P.
La distance entre F1
et F2 est a = 0,8 mm. Un écran E parallèle à P est placé à la distance D =
2,4 m de P.

1.La fente est éclairée dans un premier
temps par une lumière monochromatique de longueur d’onde λ
1.1-Quelle
est la différence de marche au point M de l’écran E tel que OM=x=12,6mm.
1.2-Le
point M étant la 7eme frange brillante (la frange centrale numérotée 0), en
déduire la longueur d’onde λ de la radiation utilisée ?
2.Un point P du champ d’interférence est tel
que la différence de marche est égale à 3,3 nm. Déterminer l’ordre
d’interférence du point P. en déduire la nature de la frange correspondante
lorsque la longueur d’onde de la lumière émise par les sources est égale
a :
2.1- λ=0.55μm ?
2.2- λ=0.508 nm ?
3.La fente est éclairée en lumière
blanche. Quelles sont les longueurs d’onde des radiations appartenant au
spectre visible pour lesquelles une frange obscure se forme au point N, sur E,
a la distance ON=x= 9 mm de la frange centrale ?
On donne pour le spectre visible :
0,4μm<λ<0,8μm
EXERCICES VII :
Situation
problème
Un vendeur
voudrait faire la commande de plusieurs lampes pouvant éclairer de manière
continue (mode normal) et de manière intermittente (mode stroboscopie). Avant
de valider la commande, il a demandé deux échantillons de lampes qu'il a
confiées aux élèves de terminale pour vérifier les caractéristiques indiquées
sur la plaque signalétique (document 1).
Une fois au laboratoire de l’établissement les élèves réalisent les expériences
suivantes :
Expérience 1
Ils observent en mode stroboscopique la surface de l'eau sur laquelle un
vibreur provoque les perturbations.
Un dispositif approprié a permis de déterminer la célérité c de la
vibration dans l'eau.
Dans cet éclairage, ils observent des rides circulaires immobiles
concentriques. La mesure de la distance entre la 1ère et la 21e ride a donné
une distance d.
Expérience 2
En éclairage continu (mode normal), Ils éclairent la surface du liquide avec
les deux lampes situées à une hauteur h de la surface d'un liquide au
repos.
 Les lampes sont distantes de a.
(figure ci-dessus) Ils constatent qu'un flotteur supposé ponctuel placé au
point A est invisible.
Les lampes sont distantes de a.
(figure ci-dessus) Ils constatent qu'un flotteur supposé ponctuel placé au
point A est invisible.
Document 1 : Plaque signalétique
Mode par intermittence
Fréquence d’émission des éclairs fe=20Hz
Mode continu
Lumière de longueur d’onde λ=580nm
Informations utiles
La commande est validée lorsque les deux caractéristiques sont conformes.
Le flotteur est invisible lorsqu'il se trouve à un point sombre.
Données: C = 0,4 m/s, OA = 14,925 cm, h = 3m, a = 0,116 cm, d = 20 cm
En exploitant les informations ci-dessus et à l'aide d'une démarche
scientifique, I
1. Aide les élèves à vérifier la conformité de la fréquence des éclairs des
lampes en mode stroboscopique.
2. Examine si la commande doit être validée ou non.
CORRIGES
.
EXERCICE I :
1- On observe un phénomène d ’interférences
lumineuses en tout point d ’un écran où se superposent les 2 faisceaux lumineux
issus des 2 sources secondaires S1 et S2. Ces 2 faisceaux
lumineux issus d’une même source ponctuelle S sont cohérents. Si les 2
vibrations qui interfèrent sont en phase, l’amplitude de la vibration est
maximale, les interférences sont dites constructives et sur l’écran on a une
raie brillante. Si les 2 vibrations qui interfèrent sont en opposition de
phase, l’amplitude de la vibration est nulle, les sont destructives et sur
l’écran, on a une raie sombre interférences
2- Pour atteindre le point O, les vibrations
lumineuses parcourent la même distance qu'elle prenne le chemin [1 ] ou le chemin [2 ]. La
différence de marche est nulle. Les 2 vibrations qui interfèrent en O sont
alors en phase : frange brillante et interférences constructives.

3-
l’interfrange i est la distance séparant les milieux de deux franges
consécutives et de même nature.
Pour les franges brillantes : ![]()
Pour les franges sombres : ![]()
![]()
4- calcul de l'interfrange : λ = 633 nm =
6,33 10-7 m D= 4 m; a = 5 10-4 m
i = 6,33 10-7 *4 /5 10-4 = 5,06 mm.
EXERCICE II:
1- Une lumière monochromatique
ne contient qu’une seule radiation de longueur d’onde l bien définie.
2- schéma :
3-
a-On observe sur l’écran des
raies alternativement brillantes et sombres appelées franges.
La frange située sur la médiatrice de F1 et F2 (frange
dite « centrale ») est brillante.
Les raies visibles sur l’écran sont parallèles aux fentes.
(le contraste entre les franges sombres et brillantes
est d’autant meilleur que le caractère monochromatique est réalisé).
b-
La position de la frange brillante n°4 est :
x=4.i=OM (i=interfrange),
soit:
![]()
4.a/L’abscisse de la 4ème frange obscure est :
![]()
D’où la longueur d’onde cherchée
![]()
b/ La position de la frange brillante du nouveau
système est :
x=4.i’=4.1,54.10-3=6,16.10-3m=6,16mm.
EXERCICE III :
1.
2..![]()
AN : d=1x100/2=50mm
3.i=λD/a=650x10-9x2/10-3=1300x10-6=1,3mm
4. d=d2-(d1+e(n-1))=d2-d1-e(n-1)=ax/D -e(n-1)
Pour la frange brillante, d=0 =>ax/D=e(n-1) => x=De(n-1) /a=2x100.10-6x (1,5-1)
=100.10-6=0,1mm
L’ensemble des franges se déplace du côté de la lame d’une amplitude
x=0,1mm.
5. la différence de marche devient :
![]()
d=0 =>ax/D=-ay/d=>x=-yD/d=-3,5.10-3
x2/10.10-2=7 cm
EXERCICE IV :
1.Caractéristiques des franges
Les franges d’interférence sont
parallèles
-aux fentes F1 et F2
-Elles sont dites délocalisées parce
que leur existence ne dépend pas de la position de l’écran ; on les
observe en tout lieu du champ d’interférences, que l’écran soit rapproché,
éloigné ou incliné.
2.La distance comprise entre la troisième frange brillante et la
cinquième frange brillante situées de part et d’autre de la frange centrale
correspond à 8 interfranges.
d=8i=8λD/a =>λ=ad/8D=1,5.10-3x6,4.10-3/8x2=0,6μm
3. La superposition d’une lame de verre sur un trajet lumineux agit
comme si ce trajet lumineux s’allonge de de e(n-1).
d’=d2-(d1
+e(n-1)) =d2-d1-e(n-1) = ax/D - e(n-1)
La frange centrale correspond a d=0 => ax/D = e(n-1) =>x= (n-1) eD/a =
(1,5-1) x4,8.10-6 x2/1,5.10-3=3,2 mm.
La frange centrale se déplace dans le sens des abscisses positives côté
de la lame de verre d’une amplitude x=3,2 mm.
4.1-On observe deux systèmes de franges colorées ayant une même
frange brillante centrale. Ce système, généralement décalé, présente quelques
coïncidences.
4.2- A la coïncidence, les abscisses des milieux de franges sont
confondues.
x1=x2
avec x1=k1i1=k1λ1D/a et x2=k2i2=k2λ2D/a
k1i1=k1λ1D/a=k2i2=k2λ2D/a <=> k1λ1=k2λ2 <=>42 k1=60k2
La première coïncidence a lieu pour les plus petites
valeurs de k1 et k2
k1=10 et k2=7
EXERCICE V :
1. Phénomène
d’interférences lumineuses.
2. Les
sources lumineuses doivent être synchrones Þ elles doivent avoir la même fréquence.
Les
sources lumineuses doivent être cohérentes Þ elles doivent garder un déphasage constant
3. ![]()
4.
L’interfrange i est la distance entre les centres de deux franges consécutives
de même nature.
5. ![]() =1,3.10-3m
=1,3.10-3m
6-1 ![]()
6-2 d = 0 est de la forme d = kl avec k = 0 Î Z donc l’interférence est constructive et la frange
est brillante
7. ![]() k=1 ϵ Z
k=1 ϵ Z
Donc l’interférence est destructive et la frange
est sombre
8.![]()
Donc la frange centrale se déplace
du côte de S2 d’une distance de 2x10-3m.
EXERCICE VI:
1.1- ![]()
x=12,6mm =>d =0,8x12,6/240=0,042 mm
1.2-d=6i=6λD/a =>λ=da/6D=12,6.10-3x0,8.10-3/2,4=4,2
μm
2.1- L’ordre d’interférence
P=d/λ=3,3/0,55=6.
Donc d=kλ
avec k=6
P est sur une frange brillante.
2.2- L’ordre d’interférence
P=d/λ=3,3/0,505=6,5.
Donc d=(k+1/2)λ
avec k+1/2=6,5.
P est sur une frange sombre.
3. Longueurs d’onde des radiations appartenant au spectre visible
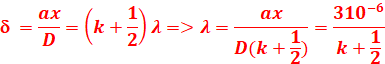
![]()
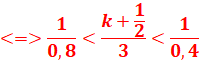
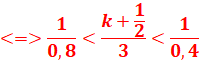
![]()
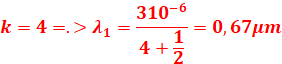
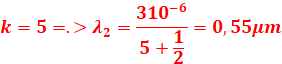
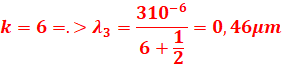
EXERCICE VII:
Il s’agit d’exploiter la fréquence de la vibration à la surface de l’eau.
Pour cela, nous allons :
• Déterminer la longueur d’onde sur la surface de l’eau ;
• Calculer la fréquence des ondes,
• Exploiter la condition de l’immobilité apparente
• conclure.
1.1. Détermination de la longueur d`onde
d=(21−1)λ⇒λ=d/20
AN : λ=20/20=1m
1.2. Détermination de la fréquence des ondes.
λ=CT⇒λ=Cf,
soit f=Cλ
AN : f=0,40,01=40Hz
1.3. Exploitation de la condition d'immobilité apparente.
fe=fk pour k=2,
on a fe=20Hz
1.3. Comparaison :
Parmi les fréquences des éclairs qui immobiliseraient les ondes à la surface de
cette eau, on a la fréquence dc 20 Hz.
Conclusion : la fréquence des éclairs peut être conforme
2. Il s'agit de calculer l’ordre d`interférence du point A :
Pour cela, il faut :
• Calculer l'interfrange.
• Calculer son ordre d`interférence
• Conclure.
1.1. Calcule de l’interfrange :
i=λha
AN : i=1,5×10−3m
1.2. Exploitation de l’expression dc la position de A pour calculer son ordre
d'interférence
OA=Pi⇒P=OAi
AN: P=99.5
P est demi-entier, donc A est sur une frange sombre
Comme les deux caractéristiques peuvent être conformes, la commande doit être
validée