ONDES STATIONNAIRES : EXPERIENCE DE MELDE
Description de l’expérience
Le
dispositif de la corde de Melde est un dispositif
classique permettant d’observer des ondes stationnaires le long d’une corde.
L’onde est ici observable à l’œil nu, puisqu’il s’agit d’un déplacement latéral
de la corde de l’ordre de quelques centimètres. Toutefois, le phénomène étant
oscillatoire et très rapide on utilise la technique de la stroboscopie pour le
ralentir en apparence et pouvoir le regarder en direct. Nous considérons une
corde tendue entre un vibreur et une poulie. Voir figure ci-dessous.

Le vibreur communique à
l’extrémité S un mouvement sinusoïdal d’amplitude a et de période T (de
pulsation ω = 2π/T, de fréquence f = 1/T). L’extrémité O est fixe, la présence de la
poulie l’empêchant de vibrer.
Observations
L’onde
incidente issu de S arrive en O, est réfléchie et retourne vers S. Lorsque la
longueur de la corde est adéquate, on observe une série de fuseaux, succession
de nœuds et de ventres.

L’onde
incidente et l’onde réfléchie se superposent et c’est cette superposition qui
donne naissance à l’onde stationnaire. L’onde est dite « stationnaire » car
l’emplacement des fuseaux est fixe. Cela s’oppose à l’onde « progressive » dans
laquelle les positions des points d’amplitude donnée varient au cours du temps.
Mise en équation du phénomène
Prenons
l’origine en O. Le point O est immobile et son immobilité résulte de la
superposition de l’onde incidente et de l’onde réfléchie. En notant yO l’élongation du point O, cela donne :
yO=asinωt
L’élongation incidente yO,i résulte de la
propagation du mouvement du vibreur de S à O. Elle est donc sinusoïdale :
En un point M quelconque de la
corde.
a) Onde incidente
L’onde incidente arrive en M avant d’arriver
en O. L’onde met un temps Δt = x/c pour se
propager de M en O. Le mouvement de M à la date t est celui que O aura x/c
secondes plus tard, c'est-à-dire à la date t + x/c. Donc :
yM,i=asinω(t+ 𝜏 )=asin(2π/Tt+2πx/cT)
![]()
b) Onde réfléchie
L’onde
réfléchie arrive en M après avoir quitté O. L’onde met un temps Δt = x/c pour se propager de O en M. Le mouvement de M
à la date t est celui que O avait x/c secondes plus tôt, c'est-à-dire à la date
t - x/c.
Donc :
yM,r=-asinω(t- 𝜏 )=-asin(2π/Tt-2πx/cT)![]() (2π/Tt-2πx/λ)
(2π/Tt-2πx/λ)
![]()
c) Superposition
Le mouvement de M résulte de
la superposition de ces deux ondes :
yM=yM,i +yM,r= ![]() (2π/Tt+2πx/λ)-
(2π/Tt+2πx/λ)- ![]() (2π/Tt-2πx/λ)
(2π/Tt-2πx/λ)
=2acos[(2π/Tt+2πx/λ)+ (2π/Tt-2πx/λ)]/2sin[(2π/Tt+2πx/λ) - (2π/Tt-2πx/λ)]/2
=2acos2π/Ttsin2πx/λ
=2asin2πx/λcosωt
Donc :
![]()
Le facteur dépendant de la
date sin(ωt) montre que le mouvement de M est
sinusoïdal de période T (de pulsation ω = 2π/T, de fréquence f =
1/T). Le terme dépendant de l’abscisse ![]() apparaît comme l’amplitude du mouvement
sinusoïdal de M.
apparaît comme l’amplitude du mouvement
sinusoïdal de M.
Conclusion : Tous
les points de la corde vibrent à la même pulsation ω mais avec des amplitudes
qui dépendent de leur position.
Etude de l’amplitude
L’amplitude est une fonction sinusoïdale de x.
En fait l’amplitude est la valeur absolue du sinus car elle est par définition
positive. Nous allons rechercher ses minima - qui correspondent aux nœuds - et
ses maximas - qui correspondent aux ventres.
·
Recherche des minima : les
nœuds La plus petite valeur de la valeur absolue d’un sinus est zéro :
![]()
![]() avec kϵZ
avec kϵZ
La distance entre deux minimas consécutifs
correspond à :
![]()
La longueur d’un fuseau est donc λ/2.
·
Recherche des maxima
:
les ventres La plus grande valeur de la valeur absolue d’un sinus est 1
(l’amplitude d’un ventre est donc 2a) :
![]()
![]()
Le premier maxima correspond à
n =0, donc à : ![]()
La distance entre deux maximas
consécutifs correspond à :
![]()
Conclusion
Dans
le cas des cordes vibrante fixées aux deux extrémités, on obtient à la
résonnance un système de fuseaux stables. La longueur utile de la corde
est :
![]()
ou n est
le nombre de fuseaux.
Cette relation peut encore
s’écrire :
![]()
-n=1 correspond à la fréquence
fondamentale.
-les fréquences harmoniques f=nf0, correspondant aux autres valeurs
de n.
Les nœuds et les ventres sont
régulièrement espacés tous les λ/4. La corde présente un nombre entier de
fuseaux :
EXERCICES
EXERCICE I
:
1) Sur une
corde de guitare, les ondes ont une célérité c = 200 m/s. La corde a une
longueur L = 50 cm. Déterminer les fréquences fi des 5 premiers modes de
vibration de cette corde.
2) Une corde
de masse m = 0.8 g est tendue entre deux chevalets distants de L = 0,5 m. Sa
tension est F = 100 N. Calculer la fréquence f1 du mode fondamental
(n = 1) et celle f3 du mode 3 (n = 3 : deuxième harmonique).
3)Une corde de
masse m = 1 g vibre en trois fuseaux entre deux chevalets distants de L = 0,5
m. Sa fréquence est de f3 = 1200 Hz.
a) Calculer la
fréquence f1 du son fondamental que peut émettre cette corde.
b) Déterminer
la tension F de la corde.
4) On accorde
un violon a une fréquence f = 440 Hz en tirant sur une corde avec la tension F
= 400 N. La corde mesure une longueur L = 0.4 m et vibre selon le mode
fondamental.
a) Déterminer
la célérité c dans ce cas.
b) On tire sur la corde avec une nouvelle
tension F' pour qu'elle émette une note à 880 Hz.
Déterminer la
nouvelle célérité c’, puis la nouvelle tension F'. Que constate-t-on?
EXERCICE
II :
On
dispose d’une corde fine en nylon. L’une des extrémités O est attachée à un
vibreur ; à l’autre extrémité, on suspend une masse m. La corde passe en E dans
la gorge d’une poulie ; E et O sont sur la même horizontale. On notera L la
distance OE. Le vibreur est une lame mince en acier. Il est soumis au champ
magnétique alternatif d’un électroaimant alimenté par un courant sinusoïdal de
fréquence 50 Hz. L’une des extrémités du vibreur est fixe. L’extrémité O vibre.
On supposera le mouvement sinusoïdal. On déplace la poulie et lorsque L = 1,20
m, la corde se met à vibrer fortement. Elle forme six fuseaux.
On
prendra :m=5kg
μ : masse linéique de la
corde :3,92.10-3 kg.m-1
g : intensité de la pesanteur :9,8
N/Kg

1) Déterminer la
longueur d’onde associée à ce mouvement.
2) La masse
linéique de la corde est μ et la masse m. Calculer la célérité de l’onde.
3) Calculer la
fréquence du mode fondamental.
EXERCICE
III :
Deux ondes
sinusoidales, de même pulsation, se propagent en sens opposés, produisent une
onde stationnaire.
1.Montrer que
la résultante de deux ondes y1=asin(2πx/λ-ωt) et y2=asin(2πx/λ + ωt),de même pulsation, de
même longueur d’onde et se propageant en sens opposes, peut être exprimée sous
la forme :y=2asin2πx/λcos
ωt
2. Soit l’onde
stationnaire : y=2asinπx/2cos 100πt, ou x et y sont exprimés en
mètres et t en secondes.
2.1-Determiner
la fréquence, la longueur d’onde des ondes composantes.
2.2-Determiner
la distance entre deux nœuds consécutifs (point d’amplitude nulle).
CORRIGES
EXERCICE I:
1) On peut exprimer les fréquences fn
de résonnance de la corde. On sait que la distance entre deux nœuds de
vibration consécutifs d’une onde stationnaire est égale à λ/2 ou λ
est la longueur d’onde.
L=nλ/2 soit λ=λn=2L/n =>fn=c/λn=nc/2L ,
n étant le nombre de fuseaux.
n=1
f1=c/2L =200/2x0,50=200 Hz
n=2
f2=2c/2L =400/2x0,5=400Hz
n=3
f3=3c/2L =3x200/2x0,5=600 Hz
n=4
f4=4c/2L =4x200/2x0,5=800 Hz
n=5
f5=5c/2L =5x200/2x0,5=1000 Hz
2) Soit μ, la masse linéique
de la corde
μ=m/l=0,8.10-3/0,5=1,6.10-3
kg/m
La fréquence est donnée par :
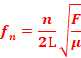
Pour le mode fondamental, n=1
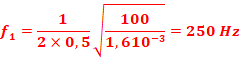
Pour la 3eme harmonique, n=3
![]()
3) f1 = f3/3
= 400 Hz ;
a-f1=n.v/2L
=>v=2Lf/n=2x0,5x1200/3=400 m/s
b-![]()
![]()
4)
a-f=c/λ=c/2L =>c=2fL=2x440x0,4=352 m/s
b-f’=2f3=c’/2L=>c’=2f’L=2x880x0,4=704
m/s
c2=F/μ
c’2=F’/μ =>F’=F(c’/c)2=400(704/352)2=1600
N
Lorsque la vitesse est multipliée par 2, la tension est multipliée
par 2 au carré.
EXERCICE II :
1.L=nλ/2 =>λ=2L/n=2x1,2/6=0,4
m
2.Tension du fil : F =mg=5x9,8=49 N
Célérité ![]()
3. f=n.c/2l =1x111,8/2.1.2=46,58 Hz
EXERCICE III :
1.y=y1+y2= asin(2πx/λ-ωt) + asin(2πx/λ + ωt)= asin(2πx/λ + ωt) - asin(ωt-2πx/λ)
=2asin[(2πx/λ + ωt) - (ωt-2πx/λ)]/2cos[ (2πx/λ + ωt) +
(ωt-2πx/λ)]/2
= 2asin2πx/λ cos(ωt)
2.1. ω=2πf
=>f=ω/2π=100π/2π=50 Hz
Par identification
2πx/λ= πx/2 =>λ=4 m
2.2.
xk= kλ/2
xk+1=(k+1)
λ/2
Δx=xk+1-
xk=(k+1) λ/2 - k λ/2=
λ/2=4/2=2 m.