LENTILLES MINCES
SPHÉRIQUES
PROPRIETES GENERALES
1-Définitions
Une lentille est un milieu transparent limité par deux calottes
sphériques ou une calotte sphérique et un plan.
Une lentille est dite mince quand son épaisseur, mesurée sur l’axe
principal, est très petite comparée aux rayons de courbure. C’est le cas des
lentilles dont le rayon de courbure est (très) grand par rapport à l’épaisseur.
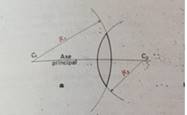
Si l’on note R1 ; R2 les rayons de courbure des
deux dioptres, C1; C2 leurs centres respectifs et e
l’épaisseur de la lentille, alors
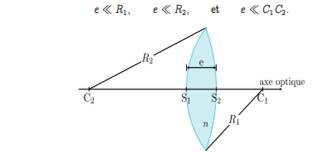
La droite passant par les centres C1 et C2 est un
axe de symétrie de révolution ; on l’appelle axe
principal de la lentille.
Par convention, on oriente l’axe optique dans le sens de propagation de
la lumière et on choisit pour origine le centre optique O.
2-Centre optique
On appelle centre optique d’une lentille le
point O ou l’axe principal perce la lentille.
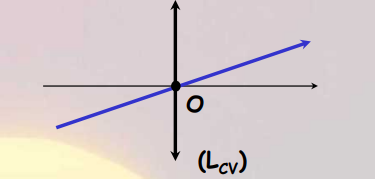
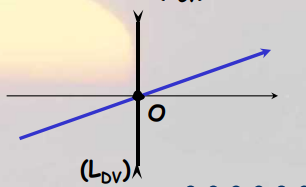
Tout rayon passant par le
centre optique d’une lentille mince traverse la lentille sans subir de
deviation.
1- Différents types de lentilles
On distingue deux familles de lentilles :
- Les lentilles à bords minces, elles sont convergentes.
-Les lentilles à bords épais, elles sont divergentes
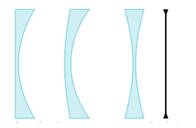

De gauche à droite : Plan concave, Ménisque divergent, Biconcave, symbole
de la lentille divergente, Biconvexe, Plan convexe, Ménisque convergent,
symbole de la lentille convergente.
LES LENTILLES MINCES CONVERGENTES
Foyers-Plans
focaux-Distances focales
a-Foyers principaux d’une lentille mince
convergente
Toute lentille mince convergente, quel que soit sa forme, possède deux
foyers principaux réels, symétriques par rapport au centre optique.
-Le foyer principal
image F’ ou la lentille fait converger les rayons parallèles
à son axe principal peut être considéré comme l’image du point A, situé à
l’infini dans la direction de l’axe principal.
-le foyer principal objet F peut être considéré comme le point objet réel dont l’image est le point
B situe à l’infini dans la direction de l’axe principal.
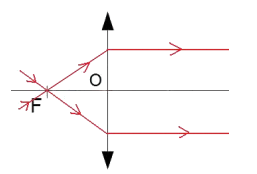
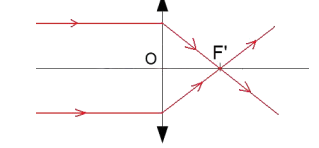
b-Plan focal image : c’est le plan
perpendiculaire à l’axe optique et contenant le foyer F’.
-Plan focal objet : c’est le plan perpendiculaire à l’axe optique et
contenant le foyer F.
c-Distance focale
On appelle distance focale d’une lentille la distance des foyers
principaux au centre optique :
f=OF=OF’
Construction géométrique des images
- tout rayon qui passe par le centre O d’une lentille n’est pas dévié (rayon de couleur verte sur le schéma)
-tout rayon incident parallèle à l’axe principal émerge de la lentille en
passant par le foyer principal image (rayon de couleur
rouge sur le schéma).
-tout rayon incident qui passe par le foyer principal objet émerge de la
lentille parallèlement à l’axe principal (rayon de couleur bleue sur le schéma).
a-L’objet est reel
Ø L’objet réel est en avant du plan focal objet
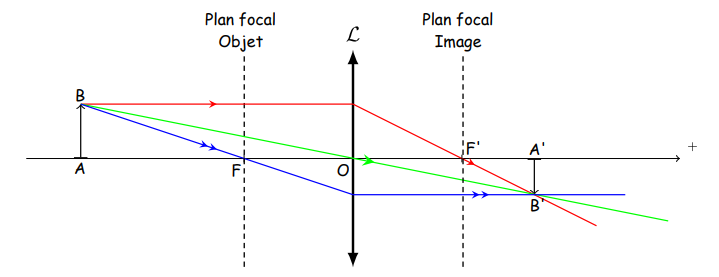
On obtient une image réelle et renversée A’B’
Ø L’objet réel est entre la lentille et le plan
focal objet
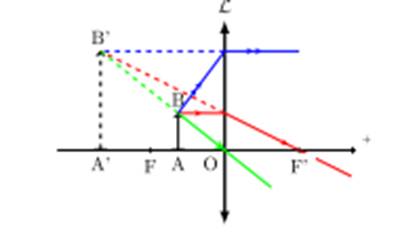
On obtient une image
A’B’ virtuelle et droit
b-L’objet est virtuel
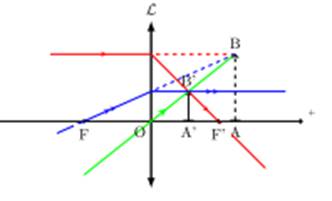
Une lentille convergente donne d’un objet virtuel une image
réelle, située dans le plan focal image, droite et plus petite que l’objet.
LENTILLES DIVERGENTES
Les foyers et les plans focaux d’une lentille
divergente sont virtuels.
Une lentille divergente a aussi deux foyers
principaux, symétriques par rapport à O : ces foyers sont virtuels
puisqu’ils se trouvent dans le prolongement des rayons lumineux.
La distance OF=OF’=f est encore appelée la distance
focale de la lentille.
Construction
géométrique des images
-tout rayon incident parallèle à l’axe principal émerge
de la lentille comme s’il venait du foyer principal image F’.
-tout rayon incident dont le support passe par le
foyer principal objet F émerge de la lentille parallèlement à l’axe principal.
a-L’objet est réel
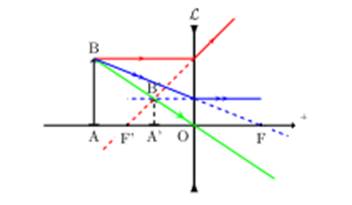
L’image obtenue est virtuelle, située entre le plan focal
image et la lentille ; droite et plus petite que l’objet.
b-l’objet est virtuel
Ø L’objet virtuel est entre la lentille et son plan
focal objet
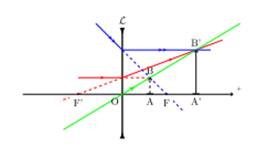
L’image est réelle, du même cote que l’objet, droite et
plus grande que l’objet.
Ø L’objet virtuel est au-delà du plan focal objet
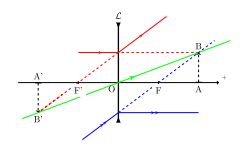
L’image est virtuelle, de l’autre cote de la lentille et
renversée. Elle peut être plus grande ou plus petite que l’objet selon que la
distance de celui-ci a la lentille est inférieure ou supérieure à 2f.
FORMULES DE CONJUGAISON
a-La relation de position

![]()
![]() .
.
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
b-La relation de grandissement

![]()
![]()
Application :
1.Un objet réel AB, de 10 cm de hauteur, perpendiculaire à l’axe
principal d’une lentille mince convergente de 20 cm de distance focale, est
place à 50 cm de la lentille ; déterminons la position, la nature, le sens
et la grandeur de l’image obtenue.
Position et Nature :
![]()
![]()
![]()
![]()
![]()
![]()
// Par
convention, on oriente l’axe optique dans le sens de propagation de la lumière
et on choisit pour origine le centre optique O.
![]()

![]()
Sens et grandeur :

Le grandissement est
négatif, l’image est renversée, sa grandeur est 0,67 fois celle de
l’objet :
Soit 10x0,67=6,7 cm
2.l’objet est virtuel et place à 10 cm d’une lentille divergente de 15 cm
de distance focale ; déterminer la nature, la position, le sens et la
grandeur relative de l’image.
Position et Nature :
![]()
L’image est réelle et
située à 30 cm de la lentille.
// ici l’objet virtuel est à droite du centre optique
donc OA>0
![]()
// lentille divergente OF’<0
![]()
// l’image est située après le centre
optique car ![]()
L’image est droite et
trois fois plus grande que l’objet.
VERGENCE DES LENTILLES MINCES
Définition
La vergence C d’une lentille est l‘inverse de la
distance focale.

Unité : la dioptrie (δ)
-les lentilles convergentes ont une convergence
positive.
-les lentilles divergentes ont une convergence
négative.
Expression de
la convergence d’une lentille mince
On démontre que :
![]()
R1,
R2 et f sont en mètre (m)
C en dioptries
Dans laquelle les rayons de courbures R1
et R2 doivent être comptés :
-positivement si la face est convexe ;
-négativement si la face est concave.
Dans le cas d’une
lentille possédant une face plane, on peut considérer celle-ci comme une
portion de sphère de rayon R2 infini d’où 1/∞=, ce qui conduit
a l’expression simple :
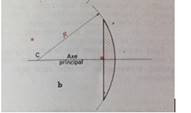
![]()
Application :
Calculons la vergence d’un ménisque divergent en
verre, d’indice de réfraction=1,5 et donc les rayons de courbure valent 25 et
30 cm.
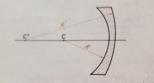
Soient R1
le rayon de la face concave et R2 le rayon de la face convexe, on
alors R1= -0,25 m et R2= +0,5m
![]()
La vergence
d’un système de lentilles minces accolées.
Considérons le cas
simple de deux lentilles convergentes L1 et L2, de
vergences C1 et C2, suffisamment minces pour que, placées
l’une contre l’autre, leurs centres optiques soient pratiquement confondus en
O.
On a :
C=C1
+ C2
Théorème des
vergences :
Un système de
lentilles minces accolées est équivalent à une lentille mince unique de même
centre optique et de vergence égale a la somme algébrique des vergences des
lentilles accolées.
EXERCICES
EXERCICE
I :
1-Sur le schéma ci-dessous,
A'B' est l'image d'un objet AB obtenue à travers une lentille mince
convergente. Donner les propriétés des 3 rayons ayant permis de construire
l'image A'B', puis décrire l'image A'B'.
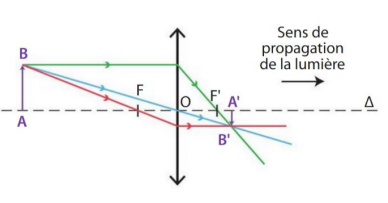
2- Un objet et une lentille mince convergente sont
placée de telle sorte que le grandissement ait pour valeur
g = - 0,80. Calculer la taille de l'image d'un objet de 5,1cm donnée par
cette lentille puis conclure.
EXERCICE II :
La vergence d’une lentille est C=5 dioptries.
1.Quelle est la nature de cette lentille ?
Quelle est sa distance focale ?
2.Où faut-il placer un objet lumineux pour que
cette lentille en donne une image quatre fois plus grande que l’objet ?
a-cas ou l’image est
virtuelle
b-cas ou l’image est
réelle.
EXERCICE III :
1°
Un objet est situé à l’infini, perpendiculaire à l’axe principal d’une lentille
convergente de vergence égale à 10δ.
1.1° Calculer la distance focale de la
lentille. Où se situe l’image
A’B’ ?
1.2° L’image A’B’ mesure 10mm. Faire la
construction géométrique traduisant l’obtention de cette image.
1.3° Calculer le diamètre apparent en radian et
en degré de l’objet AB.
2°
On accole à une lentille mince convergente de distance focale 20 cm une lentille mince convergente de 50 cm de
distance focale.
2.1° Calculer la distance focale et la vergence
du système ainsi constitué
2.2° Reprendre la question si on accolait à la
première lentille convergente une lentille mince divergente de distance focale
-25 cm. L’ensemble est-il équivalent à une lentille convergente ou
divergente ?
EXERCICE IV :
Un objet virtuel
AB, de 1 cm de hauteur, est situé sur l’axe principal d’une lentille divergente
de 5 cm de distance focale, à 3 cm du centre optique de cette lentille.
1- Préciser les propriétés de l’image par le calcul.
2-On suppose maintenant que l’objet AB, réel, est
placée à 6 cm avant le centre optique de la même lentille. Préciser les
propriétés de l’image par le calcul.
EXERCICE V :
Situation-Problème
:
MOUTAMAL le responsable d'un
laboratoire de physique a retrouvé trois lentilles dans un carton abandonné.
Sur le bordereau accompagnant ces lentilles, on peut lire : −25δ, 25δ, 40δ.
Pour identifier expérimentalement ces lentilles. MOUTAMAL a collé sur celles-ci
les index respectifs suivants : L1, L2 et L3.
Il a ensuite réparti ses élèves en deux groupes.
Le groupe 1 dispose de la lentille L1 et d'un banc
d'optique.
Expérience
réalisée.
Un objet lumineux AB est placé à 6 cm devant la lentille L1,
une image nette A’B' est obtenue sur l'écran situé à 18 cm de l'objet A.
Le groupe 2 dispose de la lentille L3
Expérience
réalisée.
La lentille L3 est utilisée comme loupe. Un élève dont
l'œil est placé au foyer image de cette lentille observe l'image A'B’ d'un
objet AB situé à 3 cm du centre optique de la loupe. La mesure de
l'angle α′ sous lequel A'B’ est vu donne α′=0,04 rad.
Après
ces trois expériences, les élèves n'arrivent pas étiqueter ces lentilles.
Donnée : AB = 1 mm.
1. En exploitant les résultats obtenus par les élèves du premier groupe et à
l’aide d'une démarche scientifique identifie la lentille L1 .
2. En exploitant les résultats obtenus par les élèves du deuxième groupe et à
l'aide d'une démarche scientifique, étiquette les trois lentilles.
CORRIGES
EXERCICE I :
1-On construit graphiquement cette image à
partir de deux rayons particuliers parmi les trois suivants :
• Le rayon issu de B passant par O n’est
pas dévié.
• Le rayon issu de B passant par le foyer
objet F émerge de la lentille parallèlement à l’axe optique.
• Le rayon issu de B parallèle à l’axe
optique émerge de la lentille en passant par le foyer image F’.
L’image A’B’ est réelle, renversée car
elle est de sens opposé à celui de l’objet et plus petite que l'objet AB.
2- Le
grandissement a pour expression :

On en
déduit la valeur de la taille de l’image : A'B' = g × AB = - 0,80 × 5,1 = - 4,1 cm L'image est renversée et plus petite que
l'objet.
EXERCICE II :
1.
C’est une lentille
convergente, C=1/f=1/5=20cm
2.
a-cas ou l’image est virtuelle
Pour avoir
une image virtuelle d’un objet réel, l’image est droite donc ![]()
![]()

![]()
L’objet est à 15 cm avant la lentille
b-cas ou
l’image est réelle.
Pour avoir
une image réelle d’un objet réel, l’mage est droite donc ![]()
![]()
![]()


L’objet est à 25 cm avant la lentille
EXERCICE III :
1°
1.1° f=1/C=1/10=10 cm.
![]()
![]()
L’image se forme dans le plan focal image.
1.2°
1.3° ![]()
2°
2.1°
![]()
![]()
C=C1+C2=7
δ
f=1/C=1/7=14,28 cm
2.2°
![]()
C=C1+C’2=5-4=1
δ
f=100cm
L’ensemble est équivalent à une lentille
convergente car C≥0.
EXERCICE
IV :
1-
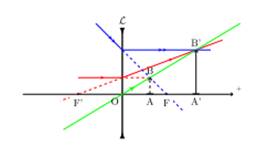
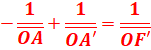
![]() < =>
< => ![]()
![]() +
+ ![]() <= >
<= > ![]()
![]()
![]()
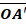
Image réelle, droite, à 7,5 cm de la lentille, haute de 2,5cm.
2-
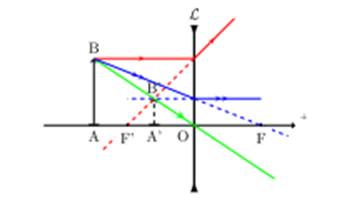
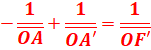
![]() < =>
< => ![]()
![]() +
+ ![]() <= >
<= > ![]()
![]()
![]()
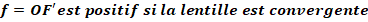
Image virtuelle, droite, à 2,73 cm avant la lentille, haute de 0,45
cm, donc plus petite que l’objet.
EXERCICE V :
Situation Problème
1. Identification de la lentille L1
Il s'agit de trouver la vergence de la lentille L1 afin de
l'identifier.
Pour cela il faut :
• Utiliser la formule de conjugaison ;
• Déterminer la distance focale de la lentille et déduire sa vergence ;
• Comparer la vergence obtenue à celles du bordereau et conclure.
![]() =>
=>![]()
![]()
Comparaison :
C1=C=25δ
Conclusion : La lentille L1 a pour vergence 25δ
2. Étiquetons les trois lentilles.
Il s'agit de trouver la vergence de la lentille L3 et exploiter les
résultats précédents pour étiqueter ces lentilles.
Pour cela il faut :
Exprimer la puissance d'un instrument optique
Utiliser la notion de puissance intrinsèque d'une loupe pour calculer la
vergence de la lentille L3
La comparer aux vergences du bordereau et conclure
Expression de la puissance d'un instrument optique
P=α′AB
Pour un œil situé au foyer principal image P=1/OF′=C
Ainsi on a: C=α′AB= 0,041×10−3=40δ
C=40δ
2. Comparaison :
C3=C=40δ
Conclusion : Il ressort que la lentille L1 a une
vergence de 25δ la lentille L2 : −25δ et
la lentille L3 : 40δ