ONDES PROGRESSIVES SINUSOIDALES
DEFINITIONS
Signal : On appelle signal une
déformation locale, souvent de courte durée.
Exemples
de signaux :
-propagation
d’un ébranlement le long d’une corde élastique.
-propagation
d’une ride circulaire a la surface de l’eau.
-propagation
d’un signal le long d’un ressort.
-propagation
d’un signal sonore.
Les
différents types de signaux mécaniques sont :
-signal
transversal : c’est un signal qui provoque une déformation dont la
direction est perpendiculaire à la direction de propagation du signal.
Exemple : cas d’une ride formée
a la surface de l’eau.
-signal
longitudinal : c’est un signal qui provoque une déformation dont la
direction est parallèle à la direction de propagation du signal.
Exemple : cas du signal se
propageant le long du ressort’
Onde : une onde est le
phénomène de propagation d’une perturbation sans transport de matière.
L’ensemble des signaux qui se propagent constitue une onde. Lorsque l’onde
nécessite la présence d’un milieu pour se propager, c’est une onde mécanique.
Onde
progressive :
L'onde progressive est le phénomène de propagation d'une perturbation, de
proche en proche, sans transport de matière mais avec transport d'énergie. La
perturbation est produite initialement par une source, comme le baffle de
haut-parleur. Cette source impose une perturbation périodique qui est
caractérisé par une double périodicité : temporelle et spatiale
Onde
progressive sinusoïdale : Une onde progressive est dite sinusoïdale si les
variations de perturbation se font en suivant la fonction mathématique sinus ou
cosinus. On peut identifier ce type de fonction à partir du graphe comportant
une alternance de vagues positives et négatives de mêmes amplitudes.
La grandeur qui la caractérise est une fonction
sinusoïdale du temps : y(t)=asin(ωt+φ)
Exemple de représentation de
la grandeur physique liée à une onde progressive périodique sinusoïdale. La
périodicité temporelle est définie par la fréquence, la périodicité spatiale
est définie par la longueur d'onde.

CARACTERISTIQUES DES ONDES MECANIQUES PERIODIQUES
Célérité d'une onde progressive sinusoïdale
La
célérité est un terme utilisé pour désigner la vitesse de propagation d’une
onde mécanique progressive.
![]()
v
est la célérité de l’onde mécanique en mètres par seconde (m/s)
d
est la distance parcourue par l’onde en mètres(m)
t
est la durée de parcourt pour franchir la distance d en seconde(s).
La célérité d'une onde périodique sinusoïdale
est constante dans le temps dans un milieu donné.Elle correspond au temps
nécessaire à un point pour parcourir la distance entre deux surfaces d'onde
identiques (amplitude maximale).
La
célérité le long d’une corde tendue dépend de la tension de la corde et de sa
masse par unité de longueur.

F
est la tension de la corde en newton (N)
![]()
Μ
est la masse par unité de longueur ou masse linéaire en kilogramme par
mètre(kg/m)
La
célérité du son dépend du milieu de propagation, elle est plus importante dans
les solides que les gaz.
Longueur d'onde
d'une onde progressive périodique
Il s'agit d'une distance qui sépare deux points
en phase consécutifs. C'est aussi une distance sur laquelle se propage une
perturbation pendant une période. Notation : λ (lambda) unité [ m ]
λ =v.T
v est la célérité en mètres par seconde(m/s)
T est la période en seconde (s)
λ est la longueur d’onde en mètres (m)
Equation de l’élongation d’onde
périodique sinusoïdale
Le retard :
On considère une onde mécanique se propage dans
un milieu unidimensionnel sans amortissement, on crée une déformation à 𝑺
l’une de extrémités d’une corde à l’instant 𝒕𝟎=𝟎.
Cette perturbation se propage avec la vitesse 𝐕 et atteint un point M1
à l’instant 𝒕𝟏, et a l’instant 𝒕𝟐 elle atteint un point 𝑴𝟐 qui répète le même mouvement de 𝑴𝟏 avec un retard 𝛕 .


Si yM1(t)=a
sinωt=asin(2π/T) t
L’onde se propageant vers la droite avec
une celerite v.
L’equation d’un point M2 situ a
une distance SM=d de S est :
yM2(t)=a
sinωt=asin2π/T t= a sinωt=asin2π/T (t-x/v)
= a sinωt=asin (2π/T t -
2πx/vT )
= asin (2π/T t - 2πx/λ )
car λ=vT
Donc :
![]()
Cette expression illustre la double periodicité d’une onde progressive sinusoidale : l’élongation du point M est une fonction du temps t et de
l’abscisse x.
-lorsque x est constant, l’élongation est une fonction sinusoidale du temps.cela traduit
le mouvement du point M du milieu de propagation : la période temporelle est T.
-lorsque t est constant, l’élongation est une fonction sinusoidale de l’abscisse x, cela
traduit l’aspect géométrique du milieu de propagation à une date t : la période
spatial est λ.
Etat vibratoire de deux points :
La différence de phase entre deux
points M et N situés respectivement à des abscisses xM et xN
est :
![]()
-Points
en phase
Deux points sont en phase lorsqu’ils ont
à chaque instant le même déplacement.
Ils
sont séparés les uns des autres par une distance égale à kλ.
Dans
le cas d’une onde sinusoïdale à
la surface d’un liquide, tous les points situés sur une même ride en phase.
Deux points M et N sont en phase
si :
![]() avec k
avec k ![]() Z
Z
-Points
en opposition de phase
Deux
points sont en opposition de phase s’ils ont à chaque instant des déplacements
opposés.
Deux points M et N sont en opposition
phase si :
![]() avec k
avec k ![]() Z
Z
SUPPERPOSITION DES ONDES PROGRESSIVES DE FAIBLE AMPLITUDE
Une des propriétés la plus basique des ondes
est la possibilité pour deux ondes de se combiner en une seule onde dont la
perturbation résultante est donnée par le principe de superposition.
Principe
de Superposition :
Quand une ou plusieurs ondes sont
simultanément présentes en un point de l’espace, à un instant donné, la
perturbation résultante du milieu, en ce point et à ce même instant, est la
somme des perturbations de chaque onde la somme des fonctions d’onde
individuelle.
Interferences mecaniques a la
surace d’un liquide
Dispositif experimental
Le dispositi experimental utilisee est une
cuve a ondes. Une fourche portant a ses extremites symetriques S1 et
S2 est adapte a un vibreur.
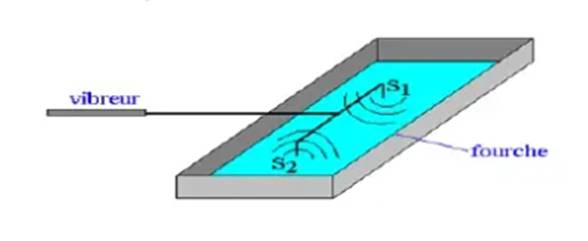
Le vibreur est la source principale, son
mouvement est transmis aux deux sources S1 et S2 qui sont
des sources secondaires engendrant des ondes progressives circulaires a la
surace du liquide.
Les sources S1 et S2 sont
animees d’un meme mouvement sinusoidal et presentent un dephasage nul, elles
sont donc :
-synchrones car elles vibrent a la meme
frequence.
-coherentes car leurs dierences de phase
est constante.
Observations
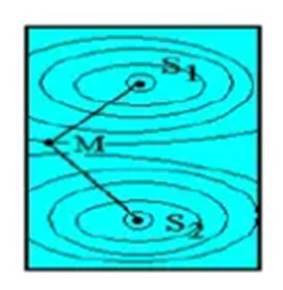
En examinant la surface de l’eau, on observe un
système de rides hyperboliques ayant leurs foyers en S1 et S2 :
ce sont des franges d’interférences. Dans certaines franges, l’eau est
animée de mouvement vibratoire verticaux très rapides avec une amplitude
maximale. Dans d’autres franges, l’eau est immobile : le mouvement
y est nul.
Les franges d’interférence n’apparaissent que
dans les régions où se superposent les rides circulaires : cette région est le champ
d’interférences.
Interprétations
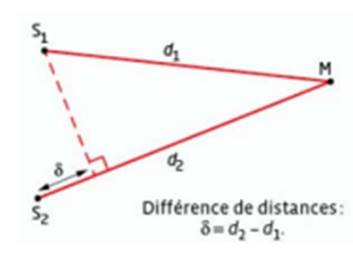
Soient
deux ondes issues des points S1 et S2. Le point M est
situé à une distance d1 de S1 et d2 de S2.
A l’instant t. le point
M subit :
·
Du
fait de l’onde issue de S1, une vibration d’amplitude : y1(M)=asin(ωt -𝜏 )= asin (2π/T t - 2πd1/λ )
·
Du
fait de l’onde issue de S2, une vibration d’amplitude : y2(M)=asinω(t- 𝜏 )= asin (2π/T t - 2πd2/λ )
On a : y(M)= y1(M)+ y2(M)=
asin (2π/T t - 2πd1/λ ) + asin
(2π/T t - 2πd2/λ )
=2asin[(2π/T t - 2πd1/λ
)+ (2π/T t - 2πd2/λ )]/2cos[[(2π/T t - 2πd1/λ
)- (2π/T t - 2πd2/λ )]/2]
=2asin[2π/T t - 2π/λ (d1
+ d2 )]cos[π/λ(d2-d1)]
=2a cos[π/λ(d2-d1)]sin[2π/T
t - 2π/λ (d1 + d2)]
=Asin(ωt+Փ)
Donc :
![]() )
)
y(M)
est une onde sinusoïdale :
-d’amplitude :
![]()
- de phase : Փ ![]()
La
différence des distances parcourues par les deux ondes δ=d2-d1 est appelée différence
de marche.
Le rapport p= δ/λ est
appelé ordre d’interférence.
-lorsque les deux ondes arrivent en phase en M,
-ces deux ondes s’ajoutent leurs effets et le
point M est sur une ligne d’amplitude maximale.
A
est maximal <=.> ![]()
![]() < =>
< => ![]()
< => ![]()
La
différence de marche est égale à un nombre entier de longueurs d’onde :
![]()
Leurs
superpositions conduit à des interférences constructives.
-lorsque
les deux ondes arrivent en opposition de phase en M, leurs effets se détruisent
et M est sur une ligne d’amplitude nulle
A=0 <=> ![]()
![]() => d2-d1=(2k+1)λ/2
=> d2-d1=(2k+1)λ/2
La
différence de marche est égale à un nombre impair de la demi-longueur
d’onde :
![]()
Leurs
effets se détruisent et M est sur une ligne d’amplitude nulle :
l’interférence est dite destructive.
On a montré que l’amplitude d’un point du champ
d’interférence, lorsque les deux sources sont en phase est :
A=2acosπ/λ(d2-d1), cette relation définit une
famille d’hyperboles et permet de retrouver les conditions expérimentales
d’existence des franges d’amplitude maximales et nulles.
EXERCICES
EXERCICE
I :
1.Une onde progressive de période T=0,05 s se propage le long d’une tendue corde à la célérité
v=10m.s-1. Calculer sa fréquence et sa longueur d’onde.
2.Une onde sonore émise par une source de fréquence 240 Hz se propage dans l’air a la célérité v=341 m.s-1. Cette onde est-elle une onde mécanique ? justifier votre réponse et calculer sa longueur d’onde.
3.Une
corde de 15 m est soumise à une tension de 20 N. une onde transversale se
propage dans la corde a la célérité v=60 m.s-1. Calculer la masse de
la corde
EXERCICE
II :
L’équation d’une onde sinusoïdale est :
y=0,15sin(0,15x-30t), x et y sont exprimés en mètres et t en secondes.
Déterminer :
1.L’amplitude
de l’onde.
2.La
pulsation.
3.La
longueur d’onde
4.La
célérité
5.Le
sens du mouvement.
EXERCICE
III :
Un vibreur est muni de deux pointes symétriques
S1 et S2 distantes de d=3,3 cm. il produit des ondes
progressives a la surface de l’eau d’une cuve à la fréquence f=20 Hz. La
célérité de ces ondes est v=0,3 m/s. Des interférences s’établissent à la
surface du liquide.
1.
Quelles conditions doivent vérifier les sources S1 et S2 ?
2.Calcler
la longueur d’onde des ondes progressives produites.
3.Donner
la condition, pour qu’en un point M de la surface du liquide, distant de d1
de S1 et de d2 de S2, il y ait :
-interférences
constructives
-interférences
destructives
4.Combien
de franges d’amplitude maximale pourront s’établir ?
EXERCICES
IV :
Deux haut-parleurs H1 et H2
sont placés face à face, à une distance d=120 cm l’un de l’autre. Ils émettent
le même son, de fréquence f=1600 Hz. Dans les conditions de l’expérience cson=336
m/s.
a-Déterminer la longueur d’onde λ du son émis.
b- Un microphone M est place en un point du segment reliant
les haut-parleurs, à la distance x de H1. Exprimer les distances H1M
et H2M et la différence de marche d =H2M-H1M
en fonction de x et d.
c.
A quelle condition le son capté par le microphone a-t-il une amplitude minimale
(interférence destructive) ? Maximale (interférence constructive) ?
CORRIGES
EXERCICE I :
1. Calcul de la fréquence :f=1/T=1/0,05=20 Hz
Calcul de la longueur
d’onde : λ=cT=10x0,05=0,5 m
2.Une onde sonore émise par une source est une onde mécanique car
elle nécessite la présence d’un milieu pour se propager, ici l’air.
Sa longueur d’onde est λ=cT=c/f=341/240=1,42 m
3. Calcul de la mass linéaire de la corde :
![]()
![]()
EXERCICE II :
L’équation d’une onde sinusoïdale
est : y=0,15sin(0,15x-30t) =-0,15sin(30t-0,2x) =
asin(ωt-2πx/λ). Par identification :
1.Amplitude de l’onde : -0,15 m
2.La pulsation : ω=30 rad/s
3. Longueur d’onde :
- 2πx/λ=-0,2x=>- 2π/λ= -0,2 =>λ=2x3,14/0,2=31,4
m
4 la célérité : λ=cT=>c=λ/T=30λ/2π=150
m/s
4.Le sens du mouvement : vers la gauche.
EXERCICE III :
1. Conditions :
-synchrones car elles vibrent a
la meme frequence.
-coherentes car leurs
differences de phase est constante.
2.La longueur d’onde :λ=cT=c/f=0,3/20=0,015
m
3.
-interférences constructives : d =d2-d1=kλ=0,015k
-interférences destructives : d=d2-d1=(2k+1)λ/2 =0,0075(2k+1)
4.La condition de vibration maximale est d2-d1=kλ
L’inegalite |d2-d1|<S1S2
implique -S1S2<kλ<S1S2 <=>-S1S2/λ<k<S1S2/λ
<=>-3,3/1,5<k<3,3/1,5<=>-2,2<k<2,2
k=-2;-1;0;1
et 2 donc 5 franges d’amplitude maximale.
EXERCICE IV :
a-λ=v/f=336/1600=21 cm
b-On a H1M=x et H2M=d-x donc d=d -x=d-2x
c-Les interférences sont constructives si : d=kλ=0,21k (avec k entier
relatif).
Les interférences sont destructives si : d=(k+1/2)λ=0,21(k+1/2) (avec k
entier relatif).
d-
Pour x=39 cm, on calcule d=0,42 m=0,21k
avec k=2 qui est entier. On est dans le cas d’interférence constructives et le
signal est donc a une amplitude maximale.
Pour x=86,25 cm, d=-0,525
m=0,21k avec k=-2,5 qui est demi-entier, il y a interférences destructives.
Pour x-63,5 cm, d=-0,07
m=0,21k avec k=-0,33 qui n’est ni entier, ni demi-entier, il n’y a ni
interférences destructives, ni interférences constructives.
Pour x=107 cm, d=-0.94
m=0,21k avec k=-4,5 qui est demi-entier, il y a interférences (presque)
destructive