LE PRISME

- .

Définition, description et rôle.

Définition et description.

Un prisme est un milieu transparent limité par deux plans non parallèles appelées faces du prisme.

Les faces d’un prisme font entre elles un angle A appelé angle du prisme, leur intersection est l’arrête du prisme.

Rôle du prisme.

· Expériences :

1) Effet du prisme sur une source monochromatique (une seule couleur)

Sur une face principale d’un prisme, envoyons une source de lumière monochromatique, un écran étant placé en arrière du prisme.

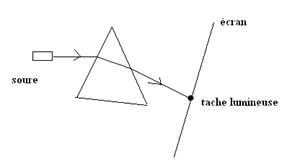
On constate que la lumière est déviée vers le bas du prisme et forme une tache lumineuse sur l’écran.

2) Effet du prisme sur une source polychromatique.

Envoyons maintenant sur notre prisme une source de lumière polychromatique (cas de la lumière blanche), l’écran étant toujours placé derrière le prisme.

On constate une fois de plus qu’il y’a déviation vers le bas mais aussi, la lumière est décomposée en plusieurs radiations à déviation croissante du rouge au le violet.

· Conclusion.

L’expérience montre donc que le prisme :

- Dévie vers la base tout faisceau lumineux qui le traverse.

- Décompose la lumière blanche en plusieurs couleurs (rouge orange jaune, vert, bleue, indigo, violet).

Marche d’un rayon lumineux et formules d’un prisme.

Considérons un prisme d’indice de réfraction n, d’angle A sur lequel on envoie une lumière monochromatique qui tombe au point I. Ce rayon traverse le prisme et y sort en I’, après avoir été dévié d’un angle D tel que :

i= angle d’incidence

r=angle de réfraction

r’=angle d’incidence

i’=angle de réfraction

D=déviation totale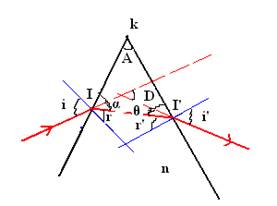

· Formules du prisme :

En appliquant la deuxième loi de Descartes en I et en I’, on a :

En I : sini = nsinr (1). En I’ : nsinr’ = sini’(2).

Relation entre A, r et r’ : dans le triangle kII’, A + α + θ = 180↔ A = 180-α-θ, or r+α =90°, α=90-r et

r’+θ = 90°, θ = 90-r’, d’où A =180- (90-r) - (90-r’) = r + r’, A =r + r’ (3).

Déviation totale: Elle est égale à la somme des déviations sur chaque face du prisme. D = D₁+ D₂, or

D₁ = i-r et D₂ = i’-r’, d’où D =( i-r)+( i’-r’) = (i+I’)-(r+r’) = (i+I’)-A car A = r+r’. D = (i+I’)-A (4).

Les formules du prisme sont donc:

sini = nsinr (1)

nsinr’ = sini’ (2)

A =r + r’ (3)

D = (i+i’)-A (4)

Remarque :

- Pour que le rayon émerge du prisme, il faut que r’≤λ (λ étant l’angle de réfraction limite) tel que sinλ = n₁/n₂.

- Lorsque les angles sont petits, sini≈i, sinr≈r, les formules du prisme deviennent.

i = nr (1)

nr’ = i’ (2)

A =r + r’ (3)

D = (i+i’)-A =nr+nr’-A= n(r+r’)-A=nA-A = A(n-1)(4)

Ø Les conditions d’émergence

-condition à imposer à l’angle du prisme

A l’entrée du prisme (milieu plus réfringent que l’air), la réfraction a toujours lieu et l’on a nécessairement r≤ λ . La condition d’émergence sur l’autre ace est r’≤ λ. En aoutant membre a membre on a :

A ≤2 λ

Pour que certains rayons puissent traverser le prisme, il faut que l’angle du prisme soit inferieur ou au plus égal au double de l’angle limite.

-condition à imposer à l’angle d’incidence

La valeur de l’angle d’incidence en dessous de laquelle les rayons ne traversent pas le prime est i0 telle que :

sini₀ = nsin(A- λ)

Ø Influence de l’angle d’incidence sur la déviation.

L’expérience montre que la déviation dépend de l’angle du prisme, de l’angle d’incidence et de l’indice du prisme. Elle varie avec l’un des paramètres lorsque les autres sont constants.

La déviation passe par un minimum D_m, au minimum de déviation,

i=i’↔r=r’ alors D_m = 2i-A↔

i = (D_m +A)/2.

A = r+r’ or r=r’↔A = 2r↔r = A/2. On sait que sini = nsinr↔

Le phénomène d’arc-en-ciel.

Le phénomène d’arc-en-ciel résulte de la décomposition de la lumière du soleil par des gouttelettes d’eau présentes dans l’atmosphère. Cette décomposition donne toutes les couleurs du spectre visible de la lumière blanche.

EXERCICES

EXERCICE I :

Un prisme possède un angle au sommet de 60° et l’indice de son verre est n = 1,51. Un rayon lumineux sort en J de ce prisme en émergence rasante, c’est à dire que l’angle de réfraction i₂ en ce point est pratiquement égal à 90°.

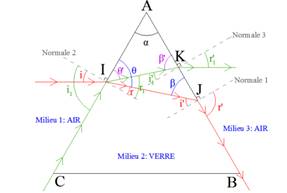
1. Déterminer l’angle d’incidence i’ en J.

2. Calculer l’angle de réfraction r en i point d’entrée du rayon.

3. Calculer l’angle d’incidence i₃ en I.

4. Calcul de l’angle d’émergence i₁ ≈ 90°

EXERCICE II :

Soit un prisme d’angle au sommet 60° et d’indice de réfraction n = 1,5. Donner les valeurs des angles d’incidence, d’émergence et de l’angle de déviation dans les cas suivants :

-incidence rasante,

-incidence normale,

-émergence rasante,

-émergence normale.

EXERCICE III :

Un prisme d’angle A et d’incidence n= 1,5, reçoit une lumière sous une incidence de 45°.

1° Pour A=60°

1.1° Calculer les valeurs de r et r’.

1.2° Calculer l’angle limite de réfraction λ et vérifier la condition d’émergence.

1.3° Calculer l’angle d’émergence i’.

1.4 Tracer la marche d’un rayon lumineux

2° Répondre aux mêmes questions pour A=90°

3° Montrer dans le cas général, que le rayon ne sortira du prisme que si A≤2λ, λ étant l’angle limite de réfraction.

EXERCICE IV :

Avec un prisme de verre (ici le verre flint) d’indice n et d’angle A=60°, on mesure la déviation minimale (Dm) subie par un rayon de lumière de couleur donnée. Pour trois couleurs : rouge, jaune et bleu, les résultats sont regroupés dans le tableau suivant :

Couleur de la lumière	Rouge	Jaune	Bleu
Dm	47,414°	48,290°	53,336°
n

1.Recopier et compléter ce tableau en calculant la valeur de n pour chaque couleur, sachant que :

2.Que peut-on dire de l’indice n ? Quel phénomène observerait-on si l’on envoyait un faisceau de lumière composée des trois couleurs ci-dessus (Rouge, Jaune et bleu) sur l’une des faces du prisme ?

CORRIGES

EXERCICE I :

1. angle d’incidence i’ en J (tracé rouge).

n₂ . sin i’ = n₃ . sin r’ => sin i’ = n₃/n₁ x sin i’ = 1/1,51 . sin 90° = 0,66 D’où: i’ ≈ 41,47

i’ ≈ 41,5° Le rayon d’incidence i’ a donc une valeur d’environ 41,5°

2. angle de réfraction r en I point d’entrée du rayon.

A=r+i’ =>r=A-i’=60-41,5=18,5

3. Calculer l’angle d’incidence i en I.

n₁ . sin i = n₂ . sin r =>sini=n₂/n xsinr=1,51/1 x sin18,5=0,479 D’où i ≈ 28,67 ≈ 28,7°
Le rayon d’incidence i a une valeur de 28,7° environ.

4. Calcul de l’angle d’émergence i₂ pour i₃ ≈ 90°(tracé vert).

n₁ . sin i₁ = n₂ . sin r₁ => sin r₁ = n₁/n₂ sin i₁ = 1,00/ 1,51 ≈ 0,662 d’ou r₁=41,47

A=r+i’₁ =>i’1=60-41,47=18,5

n2 . sin i’1 = n3 . sin r’1 =>sin r’₁ ≈ 1,51/1 . sin 18,5° =>sin r’1 ≈ 0,479 D’où: r’1 ≈ 28,7°

Si le rayon d’incidence i est en incidence rasante, le rayon qui ressort du prisme aura une valeur de 28,7°

On peut donc remarquer que si la lumière parcours un trajet dans un sens, elle subira le même trajet dans l’autre sens

EXERCICE II :

Incidence rasante :

-Angle incidence: i=90°

-Angle d’émergence :

sini=nsinr =>sinr=sini/n=1/1,5=0,667 => r=42° //ici r= λ, angle limite de réfraction.

nsinr’=sini’ <= >sini’=nsin(A-r)=1,5sin(60-42)= 0,467 => i’=28°

-Deviation: D = (i+i’)-A= (90+28)-30=58

Incidence normale : λ=42

-Angle incidence: i=0 => r=0, r’=A

-Angle emergence:

A=r+r’=r’=60 => r’=60 >λ => il n’y a pas émergence, le rayon ne sort pas du prisme. On dit qu’l y a réflexion totale

//on ne peut pas trouver i’ tel que sini’ > λ

Émergence rasante :

-Angle d’émergence : i’=90°

nsinr’ = sini’=sin90=1 =>sinr’=1/n=0,667 => r’=42°

-Angle incidence : sini=nsinr=nsin(A-r’)=nsin(60-42)=0,46 =>i=28°

Angle de déviation : D = (i+i’)-A= (28+90)-60=58°

Emergence normale :

-Angle incidence: i’=0

-Angle émergence : i’=0 =>r’=0

A=r’+r=60 => r=60 >42(λ) => il n’y a pas émergence, mais réflexion totale

//l’angle maximum pour lequel on peut avoir une émergence est 42°

EXERCICE III :

1° Pour A=60°

1.1° sini=nsinr =>sinr=(sin45)/1,5=0,47 => r=28°

A=r+r’ =>r’=A-r=60-28=32°

1.2°

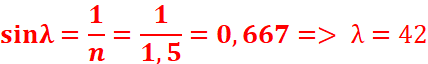
Condition d’émergence : 2 λ=84 et on a 60≤84 => A≤2 λ

1.3° angle d’émergence i’. nsinr’ = sini’ =>sini’=1,5sin(32)=0,794 =>i’=52,6°

2° A=90°

2.1° sin=nsinr =>sinr =sin45/1,5=0,47 => r=28°

A=r+r’ =>r’=A-r=90-28=62

1.2°

2.3° 2 λ=84 or A=90 est supérieur a 2 λ=84 donc il y a réflexion totale

3°

r≤ λ

r’≤ λ =>r+r’≤2 λ =>A≤2 λ

EXERCICE IV :

1.

Couleur de la lumière	Rouge	Jaune	Bleu
Dm	47,414°	48,290°	53,336°
n	1,612	1,621	1,671

2.

n varie avec la déviation.

On observerait le phénomène de dispersion de la lumière.

Avez-vous un exercice à proposer ? Cliquez-ici