OSCILLATEUR
ELECTRIQUE : CIRCUIT RLC
LES OSCILLATIONS ELECTRIQUES
LIBRES
Montage expérimental
On considère le
montage schématisé ci-dessous :
-générateur de tension continu
-condensateur de capacite C
-bobine montée en série avec un résistor R
-On place
l'interrupteur sur la position 1 de façon à charger le condensateur.
- A une date
choisie comme origine des temps (t=0), on bascule l'interrupteur sur la
position 2. Le condensateur se décharge alors dans le dipôle RL.
L’énergie électrique emmagasinée par le condensateur chargé, est
progressivement convertie en énergie magnétique par la bobine et inversement.
Ces conversions alternatives d’une forme d’énergie en une autre justifie les
oscillations électriques dont le circuit RLC est siège ces oscillations sont
dites libres car l’évolution du système ne dépend pas d’un acteur extérieur.
Etude
théorique d’un oscillateur électrique libre
Oscillations
libres avec amortissement
On s'intéresse à la décharge du
condensateur dans le dipôle RL. La loi d'additivité des tensions appliquée au
circuit s’écrit :
uC + uR +uL
=0
La charge q du condensateur est
proportionnelle à la tension uC à ses bornes : q =C.uC
Soit encore :
C’est l’équation différentielle qui
régit la variation, dans le temps, de la charge du condensateur.
Oscillations libres sans amortissement : cas limite du dipôle
LC
Le circuit LC est un cas limite
de circuit idéal dont la résistance serait nulle (R=0). L'équation
différentielle du circuit LC s’écrit :
La solution
de cette équation différentielle est de la forme :
q(t)=Qmcos(ω0t+φ)
Dans cette
relation, Qm, w0 et j sont des constantes à déterminer.
- Qm est l'amplitude q(t). Elle s'exprime en
coulombs (C).
- ω0 est la pulsation propre des oscillations électriques. C'est une grandeur
qui s'exprime en radian par seconde (rad.s-1)
- φ
est la phase à l'origine. C'est une grandeur qui s'exprime en radian
(rad).
L’expression donnant
est :
On
définit la période propre T0 des oscillations électriques libres par
la relation :
LES OSCILLATIONS ELECTRIQUES
FORCEES
Lorsqu’on
branche un générateur basse fréquence (GBF) délivrant une tension sinusoïdale
de fréquence réglable, en série avec un résistor R ,un condensateur de capacité
C et une bobine d’inductance L, le circuit RLC ainsi formé est le siège d’oscillation forcées car sa fréquence est imposée par un dispositif
extérieur.
Etude
théorique d’un dipôle RLC
Soit i(t)=Imcosωt , alors u(t)=e(t)=Umcos(ωt
+φ),
La loi d’additivité des tensions appliquée à la figure ci-dessus
donne : -e(t) +uL+uR+uC=0 => u(t)=e(t) =uL+uR+uC
Soit : 
En tenant compte des expressions :
Ri=RImcos ωt
On a :
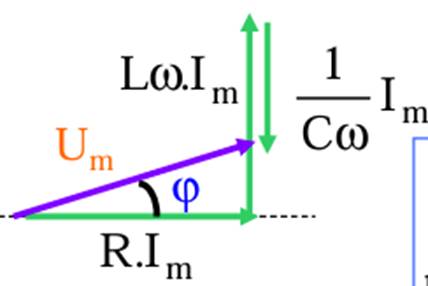
Construction
de Fresnel
La tension u(t), somme de trois tensions sinusoidales de même fréquence est donnée
par : u(t)=Umcos(ωt
+φ), La fonction sinusoïdale u(t) = Um.cos(ωt+
φ) est représentée par un vecteur (dit de Fresnel)
- de longueur Um
- faisant par rapport à l ’axe horizontal à instant
t=0 un angle
• à instant
t=0 un angle φ
• à instant t un angle (ωt+ φ)
-tournant dans le sens trigonométrique à la vitesse
angulaire ω
La construction de Fresnel donne :
Caractéristiques
du dipôle série RLC
·
Impédance :
L’impédance d’un
circuit RLC est donnée par :
·
Déphasage :
Deux relations
permettent d’établir le déphasage φ de la tension par rapport au
courant :
-si 
la tension
est en avance de phase sur le courant(φ>0) l’effet inductif est plus important que l’effet
capacitif,
- si 
la tension
est en retard de phase sur le courant(φ<0) l’effet capacitif est plus important que l’effet
inductif,
- si 
la tension
est en phase avec le courant(φ=0) les effet inductif et capacitif se compensent. Ce
cas survient à la résonnance d’intensité.
Résonnance d’un circuit RLC
Il y a résonnance d’intensité
quand la fréquence du générateur est égale à la fréquence propre du
dipôle :
La
condition de résonnance 
implique :
-
-
-
Dans un circuit RLC série, à la
résonnance d’intensité, l’impédance est minimale et égale à la résistance,
l’intensité efficace du courant est maximale, et la tension et le courant sont
en phase.
Bande
passante a trois décibels
La bande passante à trois décibels d’un dipôle RLC
est l’intervalle de fréquence pour lequel la puissance P transmise au dipôle
est supérieure ou égale à la moitié de sa valeur PR a la résonnance.
Aux limites de la bande passante :
La puissance étant proportionnelle au carré de
l’intensité, les limites de la bande passante sont telles que :
La bande passante à -3dB correspond donc aux valeurs des fréquences pour
lesquelles I(t) est supérieure ou égales à 
Les fréquences limites sont telles que :
En utilisant l’expression de Z, on obtient les
équations :
Les pulsations limites ω1 et ω2
sont les solutions positives de ces deux équations :
La largeur de la bande passante est donc
l’intervalle :
Elle est d’autant plus grande que R est grand
(résonnance floue)
Facteur de
qualité et surtension a la résonnance
Le facteur de qualité note Q d’un dipôle RLC est le
rapport :
C’est un nombre sans dimension qui rend donc compte
de l’acuité de résonnance (caractère plus ou moins sélectif) d’un
circuit : plus le facteur de qualité est grand, plus la résonance est
aigue. Cette grandeur s’exprime aussi en fonction des caractéristiques du
dipôle RLC :
A la résonance, le rapport des tensions aux bornes
du condensateur (et de la bobine), a celui de la tension appliquée aux bornes
du dipôle est
:
Soit :
Les tensions efficaces
aux bornes du condensateur et de la bobine peuvent donc être beaucoup plus
grandes que celle appliquée aux bornes du circuit RLC. Ce phénomène est appelé
surtension a la résonance et le facteur de qualité Q encore appelé acteur de
surtension.
PUISSANCE
ELECTRIQUE EN REGIME SINUSOÏDAL FORCE
Puissance
instantanée
I=IѴ2cosωt et u=UѴ2 cos(ωt+ φ)
P=ui=2UI cosωt cos(ωt+ φ)=UIcos φ +UIcos(2ωt+
φ) // cosacosb=1/2[cos(a+b) +cos(a-b)]
Puissance
moyenne
La puissance moyenne P est la valeur moyenne de la
puissance instantanée sur une période
U est en volts(V)
I en ampères (A)
P en watts (W)
C’est aussi la puissance active. La puissance active correspond à l'énergie par unité
de temps réellement consommée.
Le rapport entre la puissance active et la puissance
apparente est appelé facteur de puissance.
Puissance apparente
La puissance
apparente se note S et a pour définition :
S = U x I
S - s'exprime en voltampères (VA).
Si Z est
l'impédance du circuit envisagé, on peut remplacer I par le rapport U/Z. La
puissance apparente s'exprime alors par la relation : S = U2/ Z
Puissance
réactive
La puissance réactive se note Q et a pour définition
: Q = U x
I x sin φ = S x
sin φ
Q - s'exprime en voltampères réactifs (VAR).
Si X est la réactance équivalente du circuit
envisagé (selfique ou capacitif),
Elle s'exprime encore par l'expression :
Q = U2/
X
La puissance réactive correspond à de l'énergie
alternativement fournie et restituée.
Puissance
consommée par un dipôle RLC série
cos φ=R/Z et U=ZI => P=RI2
Tout l’énergie électrique consommée dans un dipôle
RLC série est absorbée par effet joule dans le résistor.
Importance du
facteur de puissance
Dans une installation électrique demandant une
puissance P sous une tension U imposée par le distributeur. L’intensité du
courant appelé est :
Et la puissance perdue par eet oule le long d’une
ligne distributrice de résistance r est :
La résistance r de la ligne étant fixée, de même que
la tension d’alimentation U et la puissance P à fournir, les pertes sont
inversement proportionnelles a 
Elles sont d’autant plus grandes que le facteur de
puissance est petit. Or le déphasage dans une installation dépend de
l’utilisateur. C’est pourquoi les sociétés distributrices d’énergie pénalisent
les installations industrielles de moyenne puissance dont le facteur de
puissance est inferieur a une certaine limite (très souvent 0,93) et qui sont
responsables d’un surcroit d’énergie non facturable dans les lignes
distributrices.
Pour relever le facteur de puissance, on utilise des
condensateurs que l’on branche en parallèle avec l’installation.
Entretien des
oscillations d'un circuit RLC série
Pour entretenir les
oscillations, il faut ajouter au circuit RLC un dispositif qui restitue à
chaque instant l'énergie perdue par effet Joule. Toutefois, il faut savoir que c'est un
dispositif à "résistance négative" qui apporte à chaque instant au
circuit RLC une puissance R.i2. Le bilan de puissance sera ainsi
nul.
dE /dt =-R.i2
+ R.i2 = 0
On aura ainsi une
énergie constante (E = Cte). Les oscillations sont entretenues de période T
égale à la période propre T0.
EXERCICES
EXERCICE
I:
On
réalise le montage ci-dessus dans lequel le condensateur est initialement déchargé
et la bobine d’inductance L et de résistance r.
Données :L=40
mH ;C=100nF ;R=100Ω ; E=10 V.
1-Etude du régime continu
L’interrupteur étant fermé et la bobine
supposée de résistance nulle (bobine idéale).
1.1-Exprimer la tension UC aux
bornes du condensateur et déduire la charge q du condensateur.
1.2-Determiner
les intensités dans chacune des branches du circuit.
2.
Etude du régime transitoire
On
ouvre l’interrupteur a l’instant t=0
21-Etablir
l’équation différentielle
22-Sachant
qu’a t=0, le condensateur est déchargé et que i=i0=-0,10 A.
déterminer les expressions instantanées de q(t)
et i(t).
On
précisera les valeurs numériques de l’amplitude, de la pulsation et de la phase
dans les deux cas.
3-On
suppose maintenant r=10 Ω expliquer physiquement ce qui se passe dans le
circuit
.
EXERCICE
II :
Entre
deux points A et B, on établit une tension sinusoïdale u = Umsinωt de
fréquence f = 50 Hz.
1°
Un appareil purement thermique, de résistance R = 100Ω, branché entre A et
B est traversé par un courant d’intensité efficace 1,2A. En déduire la valeur
numérique de Um, ainsi que l’expression numérique de u(t).
2° Une bobine de
résistance négligeable, placée seule entre A et B, laisse passer également un
courant de 1,2 A.
2 .1 Déterminer
l’inductance de la bobine.
2.2 Donner l’expression
i(t) de l’intensité du courant dans la bobine.
3° On monte en série entre A et B
l’appareil thermique ( voir 1°), la bobine ( voir 2°), et un condensateur de
capacité C = 10 μF. Calculer :
3.1 L’intensité du
courant efficace dans le circuit.
3.2 La ddp aux bornes
de chaque appareil.
3.3 Construire le
diagramme vectoriel des tensions.
3.4 Calculer la
puissance consommée par le circuit.
3°5 Déterminer la
capacité du condensateur qu’il aurait fallu utiliser pour obtenir l’intensité
maximale. Quelle est dans ce cas, la valeur en fonction du temps de l’intensité
instantanée i(t) ?
EXERCICE III :
On place en série, entre deux points A
et B, une bobine d’inductance L et de résistance interne négligeable, un
résistor de résistance R=80 Ω et un condensateur de capacite C. L’ensemble
est soumis à une tension sinusoïdale u(t)=UѴ2cos(ωt+φ) avec
U=100V.
L’intensité efficace du courant est
0,5A. Un voltmètre place entre les bornes du condensateur indique 120V.
1.Calculer l’impédance du circuit RLC
2.Sachant que l’impédance du
condensateur est supérieure a celle de la bobine, calculer la phase φ de
la tension par rapport au courant.
3.Representer sur un diagramme de
Fresnel les tensions UR, UL ,UC et U. en
déduire la tension efficace UL aux bornes de la bobine.
EXERCICE
IV :
On
établit aux bornes d’un circuit RLC série une tension sinusoïdale de valeur
efficace U=200 V
On
fait varier la fréquence N. A chaque valeur de N correspond une intensité
efficace I.
On
obtient le tableau :
|
N(Hz) |
400 |
500 |
600 |
700 |
780 |
800 |
900 |
1000 |
|
I(A) |
0,75 |
1,5 |
2,8 |
4 |
2,8 |
2,5 |
0,75 |
0,5 |
1.Tracer
la courbe de l’intensité I=f(I)
2.En
déduire le facteur de qualité.
3.Calculer
les valeurs de R, L et C.
EXERCICE V:
Situation
problème :
Un vendeur de composant électronique reçoit très souvent les plaintes de ses
clients sur la qualité des pièces et décide de vérifier les caractéristiques
des pièces restantes dans le magasin
(Document)
Il fait appel à sa fille Angélique élève en classe de terminale C pour l'aider
à faire ce travail. Une fois au laboratoire de l'établissement l'élève réalise
les expériences suivantes :
Document : Composants disponibles dans le magasin.
Résistor (R=85Ω ), bobine (1,2 H ; 15Ω); condensateur
(C=6μF)
Expérience
1
Elle monte le résistor aux bornes d'un générateur de tension constante U= 6 V,
l'intensité du courant est alors I = 0,0706 A.
Expérience
2
Elle monte la bobine et le résistor en série. Ce circuit est alimenté par un
générateur de tension constante U= 6 V. l'intensité du courant est alors I =
0,06 A.
Expérience
3
Elle monte le condensateur initialement déchargé en série avec le résister. Ce
circuit est alimenté par un générateur de tension constante. Un dispositif
approprié a permis de constater que la constante de temps du dipôle
est τ=0,5 ms.
Expérience
4
Le résistor, la bobine et le condensateur sont montés en série et alimentés par
un générateur basse fréquence (GBF) qui délivre une tension sinusoïdale. Un
oscillographe est branché et permet de suivre les variations des deux tensions.
On fait varier la fréquence délivrée par le GBF dans le circuit, les deux
courbes obtenues sur l’oscillographe sont en phase. L'intensité du courant dans
le circuit est de la forme : i(t)=Im cos(136πt)
En exploitant les informations ci-dessus et partir d'un raisonnement logique,
propose à Angélique la réponse qu'elle doit donner à son père.
Baccalauréat
C 2021
CORRIGES
EXERCICE I :
1-Regime continu
1.1-Tension aux bornes du condensateur
En continu, le condensateur de capacite C ne laisse pas passer le
courant, la bobine idéale se comporte comme un court-circuit, r étant nul dans
un premier temps =>UC=0
UC=Cq=0 => q=0
1.2- IC=0
IL=E/R=10/100=0,1
A
2. Régime transitoire
2.1-Lorsqu’on ouvre l’interrupteur, le condensateur se décharge dans
la bobine supposée idéale.
uC + uR +uL
=0
La charge q du condensateur est
proportionnelle à la tension uC à ses bornes : q =C.uC
uC + uR +uL
=0 <= >
Soit encore :
On trouve une équation différentielle de second ordre sans second
membre.
La solution est de la forme q(t)=Qmsin(ωt +φ).
Qm=CUC=CIC /Cω0=E/R
ω0=10/100x0,0158x106 =6,329.10-6 C
A t=0, q=0 <= > Qmsin(0 +φ)=0
=>sinφ=0 =>φ=0 ou π
Comme i=i0=-0,1<0 donc cosφ<0 alors φ=π
=> q(t)= -6,329.10-6sin1,58.104t en C
i(t)=dq(t)/dt= -6,329.10-6x1,58x104 cos1,58.104t=
-0,1cos1,58.104t en A
3. L’énergie électrique
emmagasinée par le condensateur chargé, est progressivement convertie en
énergie magnétique par la bobine et inversement. Ces conversions alternatives
d’une forme d’énergie en une autre justifie les oscillations électriques dont
le circuit RLC est siège ces oscillations sont dites libres car l’évolution du
système ne dépend pas d’un acteur extérieur
EXERCICE II :
1° u=Ri < =>
Umsinωt=RIѴ2sinωt <=>Um=RIѴ2=100x1,2xѴ2=169,2
V
u(t)=
169,2sin314t
2°
2 .1-
inductance de la bobine.
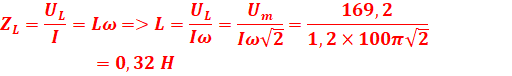
2.2 
i= IѴ2sin(ωt+φ)=1,2xѴ2xsin(100πt-π/2)
=1,69sin(314t
-π /2)
3°
3.1
L’intensité du courant efficace dans le circuit.
Um=UѴ2=>U=Um/Ѵ2=169,2x1,41
= 120V
ω=100x3,14=314
ZR=R=100
ZL=Lω=0,32x314=100,48
ZC=1/Cω=1/10.10-6x314=318,47
Ω
3.2 La ddp
aux bornes de chaque appareil.
UR=RI=100x0,5=50V
UL=LωI=0,32x314x0,5=50,24V
UC=I/Cω=0,5/10.10-6.314-=0,5/0,00318.10-5=159
V
3.3-
3.4-
Puissance consommée par le circuit.
P=UIcosφ=UIR/Z=120x0,5x100/239,83=25W
3°5
C’est la
résonnance d’intensité
LCω02=1 => C=1/Lω02=1/0,32x(314)2=3,17.10-5
F=0,32μF.
I=1,69sin314t
car φ=0 a la résonance
EXERCICE III :
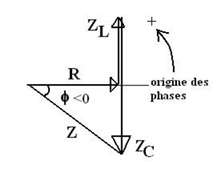
1-L’impédance Z du circuit :
Z=U/I=100/0,5=200 Ω
2-Appelons ZL l’impédance de la
bobine sans résistance ZC >ZL, comme le montre le
diagramme de Fresnel en impédance (ci-dessous), la tension u aux bornes de RLC
est en retard sur i et donc : φ < 0
3- Le diagramme de Fresnel en tension a
même allure que celui en impédance :
EXERCICE IV:
1.Traçons le graphe I=f(N): Nous obtenons la courbe de réponse en
intensité du circuit RLC Pour N=No=700Hz, I=Imax=4A, c’est la résonance
d’intensité.
Reportons sur le graphe les
abscisses des points d’ordonnée :
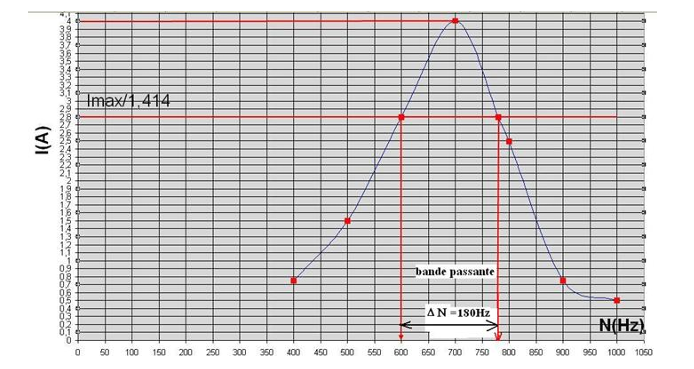
Nous obtenons la courbe de réponse en intensité du circuit RLC
2.Pour N=No=700Hz, I=Imax=4A, c’est la résonance d’intensité.
Soit N1=600Hz et N2=780 Hz
La largeur de la bande passante à 3dB est ΔN=780-600=180 Hz
Le facteur de qualité est :
Q=N/ΔN=700/180=3.9
3.R=U/Imax=200/4=50W
EXERCICE V:
Avis sur les caractéristiques
des composants électroniques
Il s'agit de déterminer les caractéristiques réelles des pièces afin
d'apprécier leur qualité.
Pour cela, nous allons 2
• Exploiter les résultats des expériences pour déterminer :
La résistance du résister ;
La résistance de la bobine ;
La capacité du condensateur :
L’inductance de la bobine.
• Comparer aux valeurs inscrites ct conclue.
l. Exploitation de l'expérience l.
Détermination de la résistance (R) du résistor
D'après la loi d'Ohm. R=UI =85Ω
2. Exploitation de l'expérience 2.
Détermination de la résistance (r) de la bobine.
U=(R+r)I ⇒r=U/I− R=15 Ω
3. Exploitation de l'expérience 3.
Détermination de la capacité (C) du condensateur.
Le dipôle constitué en série d'un résister et d'un condensateur, alimenté par
une tension constante, donne lieu à un régime transitoire de constante de temps
τ=RC⇒C =τ/R=6× 10−6 F
4. Exploitation de l'expérience 4.
Détermination de l’inductance (L) de la bobine.
• Le dipôle RLC ainsi constitué est en oscillations forcées.
•
Comme les tensions u et uR sont en phase, il
s’agit d'une résonance d’intensité.
• Condition de résonance :
LCω20=1 ⇒L= 1/Cω20=0,91
H
5. Comparaison:
|
Composant |
Caractéristiques |
Observation |
|
|
|
Inscrites |
obtenus expéri mentalement |
|
|
Résistor |
R = 85 Ω |
Rexp=85Ω |
Valeurs identiques |
|
Bobine |
r=15Ω |
rexp=15Ω |
Même valeur de la
résistance, mais les valeurs de l’inductance sont différentes |
|
Condensateur |
C=6F |
Cexp=6F |
Valeurs identiques |
Conclusion :
• Au regard des caractéristiques des composants vendus :
le résistor et le condensateur sont de bonne qualité ;
la bobine n'est pas de bonne qualité