LA REFRACTION DE LA LUMIERE

La réfraction de la lumière.

Mise en évidence.

Si nous faisons tomber un faisceau lumineux étroit d’un laser dans l’eau d’une cuve, on constate qu’au contact de la surface de l’eau :

- Une partie est renvoyée dans l’air (réflexion),

- Une autre partie pénètre dans l’eau avec changement de direction(réfraction) :

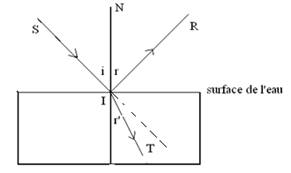
- SI est le rayon incident.

- IR est le rayon réfléchi.

- IT est le rayon réfracté.

- î est l’angle d’incidence.

- r est le rayon réfléchi

- r’ est le rayon réfracté.

- IN est la normale à la surface de l’eau.

Définitions.

On appelle réfraction le brusque changement de direction que subit la lumière à la traversée de la surface de séparation entre deux milieux transparents.

Un dioptre est la surface de séparation entre deux milieux transparents. Il est dit plan (dioptre plan) lorsque cette surface est plane.

Énoncé des lois de Descartes sur la réfraction.

Ø Faits observés.

En faisant varier l’angle d’incidence, on constate que :

- Le rayon réfracté reste dans le plan d’incidence.

- L’angle de réfraction varie dans le même sens que l’angle d’incidence.

Complétons la troisième ligne du tableau :

i(°)	0	10	20	30	40	50	60
r’(°)	0	7,5	15	22	29	35	40,30
Sini/sinr’

- Les rapports des sinus des angles d’incidence et de réfraction sont constants.

Énoncé des lois.

1^ère loi : les rayons incidents et réfractés sont dans le même plan d’incidence.

2^ème loi : pour deux milieux transparents, le rapport du sinus de l’angle d’incidence au sinus de l’angle de réfraction est constant.

Indice de réfraction d’un milieu transparent.

Indice absolue

L’indice absolu de réfraction d’un milieu est le rapport de la vitesse de propagation de la lumière dans le vide par la vitesse de propagation de la lumière dans le milieu considéré tel que :

c est la célérité de la lumière dans le vide

c = 3x10⁸m/s.

L’indice de réfraction absolu est un nombre sans unité, il est toujours supérieur ou égal à 1 exemple :

Pour l’eau, n = 4/3 = 1,33. Pour l’air, n = 1. Pour le verre, n = 1,5.

Indice relatif de deux milieux.

Par définition, l’indice relatif d’un milieu 2 par rapport à un milieu 1 est le rapport de l’indice absolu n₂ du milieu2 à l’indice absolue n₁ dumilieu1 :

En tenant compte de l’indice de réfraction, la 2^ème loi de Descartes sur la réfraction s’écrit :

n₁sini = n₂sinr’

n₁ indice du milieu d’incidence, n₂ indice du milieu de réfraction, l’angle d’incidence et r l’angle de réfraction.

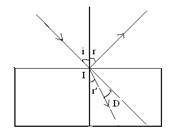
Notion de déviation :

La déviation est l’angle entre la direction du rayon incident en l’absence de tout autre milieu et sa direction dans un milieu donné, on a :

i = r’ + D alors D = i – r’.

Construction des rayons lumineux.

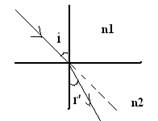
Lorsqu’un rayon lumineux passe d’un milieu d’indice inférieur n₁ vers un milieu d’indice supérieur n₂ (n₁<n₂), le rayon réfracté se rapproche de la normale.

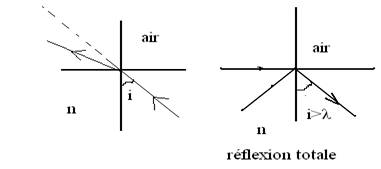
Réfraction limite

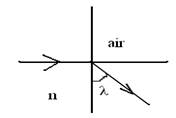
Lorsque l’angle d’incidence est i =90°, on parle d’incidence rasante et l’angle de réfraction est à sa valeur maximale qu’on appelle angle de réfraction limite ou angle critique noté λ tel que :

Réflexion totale.

Lorsqu’un rayon lumineux passe d’un milieu d’indice n₁ vers un milieu d’indice n₂ (n₁>n₂), le rayon réfracté s’écarte de la normale et si l’angle d’incidence i>λ, on observe le phénomène de réflexion totale.

Construction de l’image d’un objet donné par un dioptre plan.

Construisons l’image d’un objet A donné par un dioptre plan.

- On observe un rayon issu du point A et perpendiculaire au dioptre plan, il n’est pas dévié.

- Un rayon issu du même point A et faiblement incliné.

L’image A’ est le point de contour des rayons réfractés, l’image A’ est virtuelle.

Exemple : Un poisson dans l’eau nous semble être proche alors qu’il n’en ait rien.

Application de la réfraction.

La réfraction et surtout le phénomène de réflexion totale qui l’accompagne est très utilisé dans la confection :

- Des fontaines lumineuses.

Dans ce système, le rayon lumineux subit une succession de réflexion totale le long du jet d’eau

- Des fibres optiques.

Une fibre optique est constituée du cœur de la gaine et de l’habillage de protection. Le cœur et la gaine sont faits de verre pur d’indice de réfraction voisins avec n_C>n_g. Un rayon lumineux atteignant tangentiellement le dioptre cœur-gaine subit une succession de réflexion totales jusqu’à sa sortie.

- La réfraction permet la décomposition de la lumière blanche et de la fabrication de l’arc-en-ciel et des mirages.

EXERCICES

EXERCICE I :

1-Qu’est-ce que la réfraction ?

2-Un rayon lumineux passe de l’air à l’eau, sous une incidence i₁=45°. L’indice de réfraction de l’eau par rapport à l’air est n=1.33

-Tracer le trajet du rayon lumineux.

-Déterminer l’angle de réfraction i₂.

EXERCICE II :

1-Énoncer les lois de Descartes sur la réfraction de la lumière.

2-Un rayon lumineux passe de l’air vers un liquide d’indice n. Les angles d’incidence et de réfraction sont respectivement i=27° et r=17.5°

Calculer :

a) l’indice n de ce liquide.

b) déduire la déviation.

EXERCICE III:

L’un des rayons d’un faisceau de lumière, se propageant dans l’air, et arrivant sur une surface plane de verre.

Données : indice de réfraction du verre n verre = 1,52.

1. Schématiser la situation illustrant le phénomène de réfraction.

2. Calculer la valeur de l’angle d’incidence permettant d’obtenir un angle de réfraction de 20 °.

EXERCICE IV:

Un rayon lumineux issu d’une source laser se propage dans l’air et vient frapper la surface de polycarbonate. Le polycarbonate est un verre organique permettant d’obtenir des verres de lunette d’une extrême légèreté. L’angle de réfraction observé dans le matériau a pour valeur 21 °.

1. Représenter sur le schéma le trajet de la lumière dans ce matériau

2. Exprimer l’indice n₂ du matériau et en déduire sa valeur.

EXERCICE V:

Un pinceau lumineux cylindrique arrive sur une surface réfringente plane, séparant l’air d’un autre milieu transparent, sous une incidence de 60 ; que devrait valoir l’indice de réfraction de ce milieu pour que la déviation du pinceau réfracté soit :

a) de 15

b) de 30

EXERCICE VI:

Un prisme rectangle isocèle est immergé dans l’eau ; quelle valeur devrait avoir au moins l’indice de réfraction de sa substance pour qu’un rayon normal a une petite surface subisse la réflexion totale sur la face de l’hypoténuse ?

EXERCICE VII:

Un cube de verre d’indice N et de plan de section principale ABCD est surmonté d’une cuve contenant un liquide d’indice N’ (N>N’). Un rayon IO tombant sur la face BC se réfracte en O sur le dioptre BC. Le rayon réfracté OO’ tombant sur la face AB peut soit subir une nouvelle réfraction, soit être totalement réfléchi.

1. A partir de quelle valeur λ₀ observe-t-on le phénomène de réflexion totale ?

2. A cette valeur λ₀ correspond un angle d’incidence i₀ ? Exprimer i₀ en fonction de N et de λ₀.

3. Démontrer que ce dispositif permet, connaissant i₀ et N, de calculer N’. Exprimer N’en fonction de N et i₀. AN : N = 1,51 et i₀ = 30°.

EXERCICE VII:

Un cube de verre est immergé dans l’eau ; un rayon SI, situe dans le plan perpendiculaire aux arrêtes ABCD, aborde la face AB sous une incidence i ; quelle doit être au maximum la valeur i pour que le rayon subisse la réflexion totale en J (indice de réfraction du verre :1,5).

CORRIGES

EXERCICE I:

1- On appelle réfraction le brusque changement de direction que subit la lumière à la traversée de la surface de séparation entre deux milieux transparents.