OSCILLATEUR ELECTRIQUE : CIRCUIT RC
GENERALITES
On appelle dipôle RC un dipôle formé par l’association en série d’un condensateur de capacite
C et d’un résistor de résistance R.
q étant la valeur absolue
de la charge des armatures du condensateur de capacite C,
Pour rappel, le condensateur est formé de deux plaques métalliques planes
(de surface S) en regard et distantes de e, épaisseur du diélectrique. L’espace
entre les deux plaques est rempli par le diélectrique. Lorsqu’on alimente le
condensateur par une tension U, il se charge.
La charge q acquise par l’armature
supérieure est :
q = CU
C est la capacité du condensateur
plan (exprimée en Farad, F, ou mieux, en µF ou nF) :
ε0
: permittivité du vide
εr : permittivité relative du diélectrique
MISE EN EVIDENCE DES REGIMES TRANSITOIRES
Dispositif expérimental
On réalise un circuit électrique comprenant :
-Un générateur basse fréquence (GBF) délivrant une tension en créneaux
dont les valeurs sont successivement 0V et 6V et dont la fréquence est réglée à
la valeur f=100 Hz
-Un condensateur de capacité C
-Un résistor de résistance R.
:
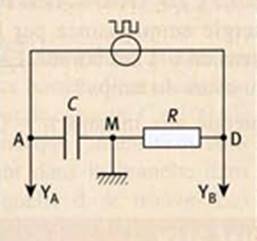
-Lorsque le
générateur délivre une tension positive u, la tension uC aux bornes
du condensateur augmente jusqu’à la valeur maximale uCmax=E : on dit que le condensateur se charge.
-Pendant les phases ou le générateur délivre une
tension nulle, la tension uC décroît, puis s’annule : le condensateur se décharge.
Le régime est transitoire
tant que la tension aux bornes du condensateur
varie. Lorsque cette tension devient
constante, le régime permanent est atteint.
Energie
électrique emmagasinée par un condensateur
L’énergie d’un
condensateur de capacité C chargé sous la tension U est donnée par la
relation :
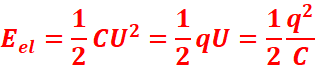
Q en coulombs (C)
C en farads (F)
U en volts (V)
Eel en joules(J)
Equation
différentielle d’évolution du circuit
u(t) = uC + uR
Cette équation différentielle
de premier ordre en uC traduit l’évolution de la tension aux bornes
du condensateur
-pendant la charge :
Les solutions sont de
la forme : 
-
-
Évolution de la
tension en fonction du temps pendant la charge.
-Pendant la décharge
Les solutions sont de la forme :
est la constante de temps du circuit (RC), elle
donne l’ordre de grandeur de la durée de charge du condensateur
Évolution de la
tension en fonction du temps pendant la decharge.
ETUDE DU
CIRCUIT RC EN REGIME SINUSOÏDAL
Soit le circuit suivant :
L'ensemble est
alimenté par une tension sinusoïdale, u(t)=e(t)=Umcos(ωt
+φ), de valeur efficace U et de fréquence 50 Hz.
Cette tension se décompose en deux tensions
partielles UR et Uc. La résistance et le condensateur sont en série
; ils sont donc traversés par le même courant d'intensité efficace I (indiqué
sur le schéma).
IR = IC = I
Définition de l’impédance
Lorsqu'une portion de circuit,
alimentée par une tension alternative, se compose exclusivement de résistances,
des condensateurs et des bobines le courant est impérativement alternatif. On
appelle alors impédance le rapport U/I. Cette nouvelle grandeur est
généralement notée Z.
U est la valeur efficace de la tension aux bornes de
la portion de circuit en volts ;
I est l'intensité efficace du courant total qui
circule dans cette portion de circuit en ampères(A)
Z est l’impédance en ohms (Ω).
Remarques :
- L'impédance, comme la résistance et la réactance,
a pour effet de s'opposer au passage du courant électrique et de le limiter.
- La relation U = Z x I traduit la généralisation de
la loi d'Ohm en alternatif.
Tension
instantanée aux bornes d’un dipôle RC
Dans un dipôle RC, la tension et l’intensité sont des
fonctions sinusoïdales de même fréquence et présentant un déphasage φ.
Soit i(t)=Imcosωt
, alors u(t)=e(t)=Umcos(ωt
+φ),
La loi d’additivité des tensions appliquée à la
figure ci-dessus donne :
u(t)=e(t) =uR+uC
Soit :
En tenant compte des expressions :
Ri=RImcos ωt
On a :
Construction de Fresnel
Le courant
étant commun aux deux éléments, on le choisit comme origine des phases.
Le vecteur 
, de longueur proportionnelle à la
résistance R, est porté par la direction de I (en phase).
Le vecteur 
, de longueur proportionnelle à la réactance Xc=1/Cω, est perpendiculaire
à la direction de I (déphasé de –π/2).
Le vecteur, résultante des deux tensions partielles, représente la
tension appliquée U. Cette résultante est ici l'hypoténuse du triangle
rectangle. Sa longueur est proportionnelle à l'impédance Z.
- La tension aux bornes de la résistance R est en phase avec le courant
et UR = R x I.
- La tension aux bornes du condensateur C est déphasée de –π/2 avec
le courant (retard de T/4) et Uc = I/Cω.
- Les deux tensions partielles sont donc en quadrature.
Caractéristiques du dipôle série RC
·
Impédance
D’après le théorème de Pythagore,
=>
·
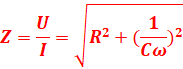
Déphasage
de la tension appliquée par rapport au courant.
L’angle φ est négatif :la tension
appliquée est donc en retard sur le courant.
Cet angle est tel que :
Ou encore :
Puissance moyenne consommée par le
dipôle RC
La tension étant en quadrature retard sur le
courant, : φ=-π/2 donc cos φ=0.
La
puissance moyenne P=0
EXERCICES
EXERCICE I :
On
envisage le circuit suivant constitué d'un conducteur ohmique de résistance R
et d'un condensateur de capacité C.
À
l’instant t = 0, le condensateur est chargé sous la tension U0 = 10
V.
On
notera :
•
uC la tension aux bornes du condensateur à l'instant t, et l'on a uc(0) = U0
•
uR la tension aux bornes du conducteur ohmique à l'instant t,
•
i l'intensité du courant à l'instant t. Cette intensité a été comptée
positivement au cours de la charge du condensateur,
• qA la charge de l'armature A du
condensateur à l'instant t.
1. Quelle relation lie uR et uC ?
2. Rappeler la relation qui lie la charge qA de
l'armature A à la tension uc.
3 .Établir la relation liant l'intensité i du courant à la
tension uc.
4. Montrer que l'équation différentielle régissant
l'évolution de uc peut s'écrire :
où a est
une constante non nulle. Donner alors l'expression de a en fonction de R et C.
.5 Une solution de cette equation est de la orme 
, A etant une constante strictement positive
En utilisant
l'équation différentielle, montrer que b = 1 /RC .
EXERCICE
II :
On réalise le circuit série du document 1 formé
d'un conducteur ohmique de résistance R = 1 kΩ, d'un condensateur
initialement neutre de capacité C, d'un générateur
idéal de force électromotrice E et d'un interrupteur K. On ferme K à la date t0
= 0.
1)
Nommer le phénomène physique qui a lieu dans le circuit.
2)
Établir l'équation différentielle qui décrit l'évolution de la tension uBD = uC
aux bornes du condensateur.
3)
La solution de cette équation différentielle est :
Déterminer
les expressions des constantes A, B et τ en fonction de E, R et C.
On
suppose qu’a t=0, uc(0)=0.
4) La courbe du document 2 représente l'évolution de uC avec le temps.
4.1) En
se référant au document 2, indiquer la valeur de E.
4.2) En utilisant le document 2, déterminer la
constante de temps τ du circuit.
4.3)
Déduire la valeur de C. 4.4) En utilisant le document 2, déterminer l'énergie
électrique emmagasinée dans le condensateur à t =1,4 ms.
4.5) Déduire la puissance électrique moyenne
consommée le condensateur entre t = 0 et t =1,4 ms.
EXERCICE
III :
Le
circuit électrique se compose d'un condensateur C en série avec une ampoule A,
tel que représenté ci-dessous.
Données
:
Valeur
du condensateur : C = 8,2 µF.
Caractéristiques
de l'ampoule lues sur son embase : UA = 130 V;
P = 60 W; d'où I =0,46 A et la résistance à chaud RA
= 282 Ω.
La
tension appliquée U est égale à 230 V - 50 Hz.
1
- Calculer la tension Uc aux bornes du condensateur.
2
- Vérifier que la tension appliquée U n'est pas égale à la somme arithmétique
des tensions partielles Uc et UA.
3
- Calculer l'impédance Z du circuit en effectuant le rapport U/I.
4
- Recalculer la valeur de Z en appliquant une autre relation
5
- Comment peut-on justifier la légère différence entre les deux valeurs de
l'impédance Z obtenues ?
6
- Calculer le déphasage ϕ de la tension appliquée par rapport au courant.
7
- Donner en millisecondes la valeur Δt du retard de la tension appliquée
par rapport au courant.
EXERCICE
IV :
Situation problème :
Jean propriétaire d'un immeuble de dix niveaux constate qu'il fait très sombre
dans les escaliers lors des coupures du courant. Il décide d’achète un kit
solaire pour alimenter les lampes installées pour éclairer les escaliers
pendant une durée donnée après coupure de courant.
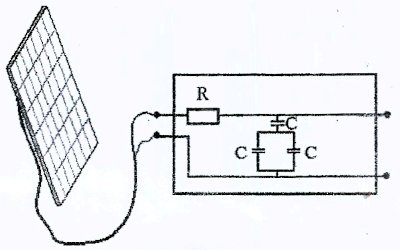
1. Le kit ( schéma ci-dessus) est constitué :
•
d'une plaque solaire comprenant 20 cellules photoémissives identiques et
montées en parallèle (les caractéristiques d'une cellule sont données sur le
document) ;
• d'un système d'accumulation d'énergie électrique comprenant un résistor et
une association de trois condensateurs identiques ( voir
ci-dessous). L'association de condensateurs correspond à un condensateur
équivalent dont la courbe de charge est représentée en annexe.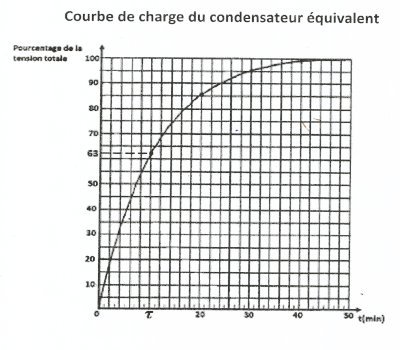
Compte tenu de la taille de la plaque,
Jean se demande si elle pourra générer une intensité de courant de 5,0 A
nécessaire pour fournir la tension convenable de charge du système
d'accumulation.
Pendant l'installation, le technicien constate qu'un condensateur est
défectueux dans le système d'accumulation.
l Document : Caractéristiques d'une
cellule
• Puissance lumineuse reçue par une cellule P=1,0W
• Rendement quantique Rd=0,575
Autres informations
Rd=nN avec N le nombre de photons incidents par unité de temps
et n le nombre d'électrons émis par la cathode par unité de temps.
L’intensité de courant générée par la plaque correspond à l'intensité de
saturation des cellules.
Données : λsoliel=0,54μm ; e=1,6×10−19C ; h=6,62×10−34J.s ; c=3,0×108m/s ; R=6,0×108Ω et 1μm=10−6m
En exploitant les informations ci-dessus et en utilisant un raisonnement
logique :
1. Examine l'inquiétude de Jean.
2. Propose au technicien la caractéristique du condensateur défectueux.
CORRIGES
EXERCICE I :
1 Relation qui lie uR et uC : uC + uR = 0.
2 Relation qui lie la charge qA de l'armature A à la
tension uc : qA = C.uC
3.Relation liant l'intensité i du courant à la tension uc.
4 Equation différentielle
régissant l'évolution de uc :
uC + uR
= 0.< => 
= >
=0
en posant 
= >
=0
5. 
Remplaçons l’expression obtenue dans l’équation
différentielle :
uC + uR
= 0 < => 
=
< => 
< => 
=>
car l’énoncé précise que A est une constante
strictement positive
EXERCICE II :
1.Le condensateur se charge.
2) équation différentielle qui décrit l'évolution de la tension uBD
= uC aux bornes du condensateur.
u(t) = uC+uR
Pendant la charge :
=Ri=Rdq/dt=RCdu/dt donc u(t) = uC+ RCduc/dt
3) La solution de cette équation différentielle est :
D’où 
avec 
4)
4.1) valeur de E.
E=12 V
4.2) constante de temps τ du
circuit.
A t=2,5 s, uc=11 V
11=12(1-e-2,5/ τ) => τ=1
4.3) valeur de C.
Τ=1/RC =>C=1/ τ
r=1/1000=10-3 F
4.4) 'énergie électrique emmagasinée
dans le condensateur à t =1,4 ms.
4.5) puissance électrique moyenne
consommée le condensateur entre t = 0 et t =1,4 ms.
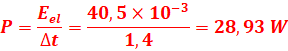
EXERCICE III :
U = 230 V - 50 Hz; Condensateur : C = 8,2 µF;
Ampoule : UA = 130 V; P = 60 W; I = 0,46 A; Résistance à chaud RA=
282 Ω.
1 - Calcul de la tension Uc
aux bornes du condensateur :
2 - Somme arithmétique des tensions
partielles Uc et UA :
Uc + UA = 180 + 130 = 310 V
Cette tension est très différente de la tension U qui vaut 230 V. Les tensions
partielles ne s'ajoutent pas arithmétiquement !!!
3 - Premier calcul de l'impédance du circuit :
4 - Deuxième calcul de l'impédance : Calcul de la réactance du
condensateur :
5 - La légère différence (4%) entre les deux valeurs de l'impédance
Z obtenues est due surtout au manque de précision sur la valeur de I.
6 - Calcul du déphasage ϕ de la tension par rapport au courant
:
7 - Calcul du retard Δt de la tension appliquée par rapport au
courant.
EXERCICE IV :
1. Il s'agit de trouver l’intensité du courant débité par cette plaque solaire
afin d'apprécier l’inquiétude de Jean.
Pour cela, nous allons :
Exploiter l'expression du rendement quantique de la cellule pour déterminer
l’intensité du courant de saturation pour une cellule.
Utiliser la loi d’additivité des courants pour déterminer l’intensité du
courant débité par la plaque;
La comparer à la valeur de l’intensité que Jean souhaite obtenir et conclure.
1.1. Exploitation de l’expression du rendement quantique et de celle de la
puissance lumineuse :
Détermination du courant de saturation d'une cellule
Rd=nN, ne=IS⇒n=ISe et P=N.h.ν⇒ N=Ph.ν
Rd=ISePh.ν= h.C.ISeλP⇒IS= eλPRdhC
AN : IS=0,25A
1.2. Exploitation de l’additivité des courants.
Détermination de l’intensité du courant débite.
I=20IS=5A
1.3. Comparaison:
I=Ijean=5A
Conclusion: Cette plaque peut bien débiter l’intensité de courant voulu par
Jean
2)- Proposons au technicien la caractéristique du condensateur défectueux :
ll s'agît de trouver la capacité du condensateur défectueux.
Pour cela, nous allons : 1 pt
• Exploiter le graphe pour déterminer la constante de temps;
• Exploiter l'expression de la constante de temps pour déterminer la capacité
du condensateur équivalent,
• Utiliser la relation de la capacité équivalente dans ce montage mixte pour
déduire la capacité d’un seul condensateur du système ;
• Conclure.
1.1. Exploitation du graphe de l’annexe
Détermination de la constante de temps τ
τ correspond au temps de chargement du condensateur jusqu'à 63% de sa
capacité totale d'accumulation.
τ=10min
1.2. Exploitation de l’expression de τ pour déterminer Céq.
Détermination de l’intensité du courant débité.
τ=RCeq⇒Ceq=τ/R
AN : Ceq=1μF
1.3. Détermination de la capacité des condensateurs
1Ceq=1C+1C+C =32 C⇒C=23Ceq
AN : C=1,5μF
Conclusion : Le technicien doit utiliser une capacité de rechange de (1,5\mu
F\)