PROPAGATION RECTILIGNE DE LA LUMIERE
DEFINITIONS
Les sources
de lumière
Les
sources de lumière sont des objets qui produisent la lumière ou qui renvoient
la lumière reçue.
On distingue deux types de sources
lumineuses :
-
Les sources de lumière primaires : Elles émettent la lumière
produite par elle-même
Exemple :
Le soleil, la bougie, la lampe tempête, les étoiles etc.
-
Les sources de lumière secondaires : Elles diffusent ou revoient la
lumière reçue.
Exemple : la lune.
Une source de lumière
est ponctuelle si ses dimensions sont très faibles par rapport à la
distance de la source à l’observateur. Dans le cas contraire on parle de source
étendue.
Les
récepteurs de lumière
Les
récepteurs de lumière sont des dispositifs sensibles à la lumière qu’ils
reçoivent.
Exemple : l’œil, les pellicules photographiques,
les plantes vertes, les photos calqueurs, etc.
Rayon lumineux, faisceau
lumineux
Un rayon lumineux est le trajet
rectiligne suivit par la lumière, il se représente par une flèche :
Un faisceau
lumineux est un ensemble de rayons lumineux, on distingue trois types de
faisceau lumineux :
-
Le faisceau convergent :
-
-
Le
faisceau divergent :
Notion d’année-lumière
Une
année-lumière (a.l) est la distance parcourue par la lumière, dans le vide, en
un an.
Les distances
astronomiques sont évaluées en année-lumière.
Exemple :
Evaluons
approximativement une année-lumière en milliards de kilomètres sachant
que :
1 an=365 jours
1 jour=24
heures
1 heure=3600
secondes
d=ct=3.108x365x24x3600=9460
milliards de km environ
1
a.l=9460 milliards de km
LA PROPAGATION DE LA LUMIERE.
On
montre expérimentalement que « dans
le vide et dans tous les milieux transparents et homogènes, la lumière se
propage en ligne droite ».
Les milieux
de propagation de la lumière.
·
Certains
milieux se laissent traverser facilement par la lumière, ils sont dits transparents.
Exemple : L’air, l’eau, du vide
NB : dans le vide, la vitesse de
propagation encore appelée la célérité est égal à :c= 3x108m/s.
·
D’autres
par contre arrêtent totalement la lumière, ils sont dits opaques.
Exemple : la terre, du bois, etc.
·
D’autres
encore empêche l’œil d’identifier l’objet lumineux : Ils sont dits translucides.
Exemple : le papier huileux, le verre dépoli, la
porcelaine.
Application
de la propagation rectiligne de
la lumière.
La
visée
Lors
de la mesure des terrains, on utilise un théodolite (appareil de mesure des
topographes) pour une meilleure mesure.
L’ombre
et la pénombre.
Ø Cas d’une source
ponctuelle.
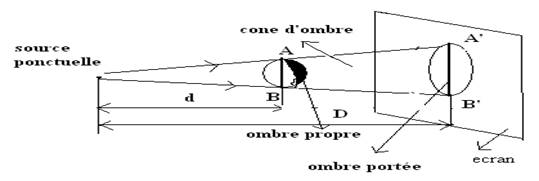
Les dimensions
A’B’ de l’ombre portée se déduisent de celles de l’objet AB par la
relation :
AB/d = A’B’/D. AB(m), A’B’ (m), d
distance source-objet (m), D distance source-écran (m).
Ø Cas d’une source
étendue
Ø L’éclipse du soleil et
de la lune.
On parle d’éclipse du soleil lorsque la terre
se retrouve dans le cône d’ombre de la lune, il y’a éclipse de la lune quand
celle-ci passe dans le cône d’ombre de la terre.
La chambre noire.
Elle donne d’un
objet AB, une image A’B’ réduite et renversée.
Les
dimensions A’B’ de l’image se déduisent de celles AB de l’objet par la
relation : AB/d = A’B’/D. Étant
la profondeur de la chambre.
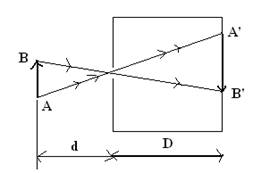
Le diamètre apparent d’un objet.
Pour qu’on objet soit vu, il faut qu’il
envoie un faisceau de rayon vers la pupille de l’observateur.
L’angle θ
sous lequel l’objet AB est vu, est appelé diamètre apparent.
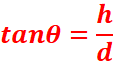
θ étant
généralement faible, tanθ ≈θ≈h/d.
EXERCICES
EXERCICE
I :
Un
disque opaque de 10 cm de diamètre est placé entre une source de lumière
ponctuelle et un écran parallèle à ce disque, a 1 m de la source et de
l’écran ; calculer le diamètre de l’ombre portée sur l’écran.
EXERCICE
II :
Calculer
la hauteur d’un poteau télégraphique sachant que son ombre mesure 5 mètres au
moment où l’ombre d’une règle verticale de 1 mètre mesure 0,62 m.
EXERCICE
III :
Dans
la reproduction d’un objet dans une chambre noire, l’objet a 15 cm de
hauteur ; l’ouverture de la chambre noire est à 80 cm de l’objet et la
profondeur de cette chambre est de 20 cm ; calculer la hauteur de la
reproduction observée sur le verre dépoli.
EXERCICE
IV :
On veut obtenir d’un édifice une reproduction
par le dispositif de la chambre noire. L’édifice à 40m de hauteur, il est situé
à 80 m de l’ouverture de la chambre. Quelle doit être la profondeur de celle-ci
pour que la reproduction ait 10 cm de hauteur ?
EXERCICES
V :
Le
centre d’un disque de diamètre d = 2cm est placé à l = 0,5 m d’une source
ponctuelle de lumière S, un écran E est placé à L = 3m de la source.
1. Quelle
est la dimension de l’ombre portée sur l’écran ?
2. Calculer
l’angle α au sommet du cône d’ombre.
EXERCICE VI :
1. L’étoile la
plus proche de nous en dehors du soleil est la Proxima du Centaure. Elle est
visible dans l’hémisphère sud. La lumière qu’elle envoie met quatre années
environ pour nous parvenir. Quelle est, en année-lumière la distance qui sépare
cette étoile de la terre ?
2. Calculer le
temps que met la lumière pour nous parvenir de la lune sachant que la distance
de la terre a la lune vaut 60 fois le rayon de la terre. (On admet que le mètre
est la dix-millionième partie du quart de la circonférence d’un grand cercle de
la sphère terrestre).
3. les ondes TV
se propage à la vitesse de la lumière
Calculer le temps mis par l’onde TV pour aller
de l’émetteur a une antenne située à 600 km.
EXERCICE VII :
En 1969, les
astronautes Neil Armstrong et Edwin Aldin ont déposé sur la lune, un réflecteur
pour rayons lasers. Ainsi, lorsqu’on émet de la terre un rayon laser vers ce
réflecteur, la lumière revient 2,6 secondes plus tard.
1.
Calculer
la distance parcourue par la lumière pour faire cet aller-retour
2.
En
déduire la distance Terre-lune.
CORRIGES
EXERCICE
I :
AB/d = A’B’/D
=>A’B’=ABxD/d
Or D=2d
donc A’B’=2AB=2x10=20 cm
EXERCICE
II :
Règle :
A’1B’1=A1B1.D/d avec A’1B’1=0,62
m et A1B1=1 m
Poteau :
A’2B’2=A2B2.D/d avec A’2B’2=
5 m
En faisant
le rapport des deux relations, on tire A2B2= A1B1x
A’2B’2/ A’1B’1=1x5/0,62=8,02m
EXERCICE
III :.
AB/d = A’B’/D. =>
A’B’=AB.D/d=15x20/80=3,75 m.
EXERCICE
IV :
AB/d = A’B’/D.
=>
D=A’B’xd /AB=0,1x80/40=0,2 m
EXERCICES
V :
1.
AB/l
= A’B’/L =>A’B’=AB.L/l=0,02x3/0,5=12cm
2.
3.
4. EXERCICE VI :
5. 1. 4 a.l
6. 2. c=d/t =>t=d/c
7.
Circonférence de la terre : πDT=2πRT
8. Dix-millionième partie du
quart de la circonférence : 2πRT x ¼.10-7= 1m
=>RT=2.107/π
9. Distance Terre-lune :
d=60RT=60x2.107/π
10. t=d/c=60x2.107/π.3.108=1,27
s.
11. 3. Calcul du temps mis par
l’onde TV pour aller de l’émetteur a une antenne située à 600 km.
12. t=600 :300000=0,002 s
13.
14. EXERCICE VII :
15. 1. d=2,6x300000=780000km
16. 2. 780000 :2=390000km