PENDULE PESANT

Description d’un pendule pesant

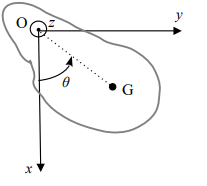
Un pendule pesant est un solide de masse m de forme quelconque mobile dans le champ de pesanteur terrestre autour d’un axe horizontal fixe ne passant pas par son centre d’inertie G. On note Oz l’axe de rotation orienté du solide et J_Δ son moment d’inertie par rapport à l’axe Oz. On suppose que la liaison entre le solide et l’axe de rotation est une liaison pivot parfaite. On néglige les frottements dus à l’air. On repère la position du solide par l’angle θ que fait la droite (OG) avec la verticale descendante (Ox).

Etude dynamique du pendule pesant

Dans le référentiel terrestre, le solide de forme quelconque est soumis à son poids P et à la réaction R du support. On suppose négligeables la résistance de l’air et les frottements au niveau de l’axe.

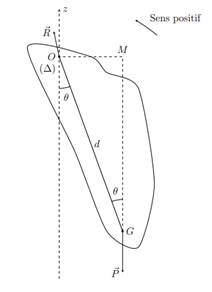
Système étudié : (S)

Bilan des forces extérieures exercées sur (S)

· Poids du système :

· Réaction de l’axe :

Application de la relation fondamentale de la dynamique en rotation :

<= >

La droite d’action de coupe l’axe (Δ) donc

On pose a=OG ou G est le centre d’inertie d système. Dans ce cas, nous avons :

<=>

<=>

C’est l’equation differentielle du pendule pesant

Pour des oscillations de faible amplitude (θ < 0,026 rad), on peut écrire en première approximation

sinθ ≈ θ en radian.

L’équation différentielle devient alors :

On pose :

On obtient :

C’est l’équation différentielle de second ordre sans second membre, les solutions sont de la forme :

Θ=θ_msin(ω₀t +φ)

Les oscillations de faible amplitude d’un pendule pesant sont donc sinusoïdales.

De pulsation propre 

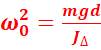
Et de période propre :

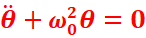
Etude énergétique du pendule pesant

a) Energie mécanique de l’oscillateur

On sait que l’énergie mécanique totale (Em) du pendule pesant à chaque instant est égale à son énergie potentielle (Ep) plus son énergie cinétique (Ec) :

Em=Ep +Ec

En négligeant les frottements,

· Au point G, position d’amplitude maximale : v=0 => Ec=0

Ep=mgz avec z=d-OG₀

=d-dcosθ=d(1-cosθ)

Ep=mgd(1-cosθ) =>

Em= mgd(1-cosθ) + 0

On suppose que le plan horizontal passant par G₀ à l’équilibre, comme état de référence de l’énergie potentielle de pesanteur, Ep = 0

· Au point G₀, position d’équilibre du pendule : z=0 , Ep=0

· Pour une position M quelconque,

Cas des oscillations de faible amplitude

Dans le cas des oscillations de faible amplitude, cosθ≈1-θ²/2

//car cosθ≈1-θ²/2 =>1-cosθ≈θ²/2

// on remplace Θ par θ_msin(ω₀t +φ) , et

//cos²x +sin²x=1

L’énergie mécanique d’un pendule pesant de faible amplitude d’oscillation est donc proportionnelle au carré de son amplitude.

Conclusion : L’énergie mécanique d’un pendule pesant non amorti est donc constante.

b) Etablissement de l’équation différentielle à partir de la conservation de l’énergie mécanique totale

^{Les frottements sont négligeables donc, il y a conservation de l’énergie mécanique.}

En dérivant les deux termes de l’expression par rapport au temps, on a :

)

//(cosu)’=u’sinu

On retrouve l’équation différentielle du mouvement du pendule pesant.

EXERCICES

EXERCICE I :

Un pendule pesant est constitué d’’une tige homogène OA de masse m, de centre d’inertie G et de longueur L pouvant effectuer un mouvement de rotation dans un plan vertical autour d’un axe horizontal (Δ) passant par son extrémité O. Soit J_Δ le moment d’inertie du pendule par rapport à l’axe (Δ).

On étudie le mouvement du pendule dans un repère lié à un référentiel terrestre suppose galiléen. On écarte la tige OA de sa position d’équilibre stable d’un angle θ_m=10 rad, dans le sens des élongations positives, puis on le l’abandonne sans vitesse initiale à l’instant t=0.

On repère la position du pendule à un instant t quelconque par l’abscisse angulaire θ. Le centre G est confondu avec G₀ quand le pendule passe par la position d’équilibre stable.

On néglige tous les frottements et on choisit le plan horizontal passant par G₀ comme état de référence de l’énergie potentielle de pesanteur (Epp=0).

Données :

Masse de la tige :m=100g ; longueur de la tige : L=0,53m

Expression du moment d’inertie de la tige par rapport à l’axe (Δ) : JΔ=1/3mL²

g=10 usi

Pour les petits angles : cosθ≈1-θ²/2 ou θ est exprimé en radians.

1. Trouver l’expression de l’energie potentielle de pesanteur du pendule pesant a un instant t, dans le cas des oscillations de faible amplitude, en fonction de θ, L, m et g( intensite de la pesanteur).

2.Par etude energetique, motrer que l’equation differentielle du mouvement s’ecrit :

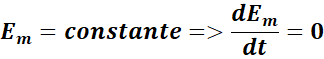
3. Calculer l’énergie mécanique totale.

EXERCICE II :

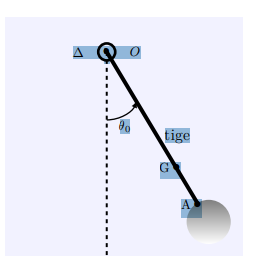
Un pendule pesant est constitué d’une boule homogène de rayon r=2,5 cm et de masse m = 200g et d’une tige homogène de même masse que la boule et de longueur L = 10r, l’une des extrémités est soudée à la boule au point A . Le système (Tige+boule ) peut tourner autour d’un axe fixe (∆) passant par le point O de l’autre extrémité de la tige . On néglige tous les frottements et on prend g = 10m/s² Le moment d’inertie du système par rapport à l’axe ∆ est J∆ = 10⁻²kg.m² . On écarte le système de sa position d’équilibre stable d’un angle de θm = 10◦ puis on le lâche sans vitesse initiale à la date t=0.

1. En appliquant la relation fondamentale de la dynamique au système, montrer que l’équation différentielle du mouvement du système s’écrit sous la forme suivante :

2. Quelle est la nature du mouvement du système ?

3. Calculer la période propre du mouvement ;

4. Déterminer l’équation horaire du mouvement de système

EXERCICE III :

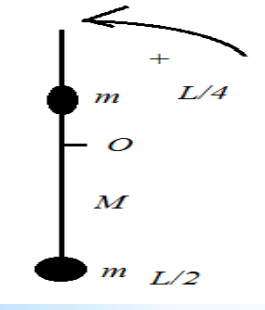
Une tige homogène de longueur L et de masse M est mobile autour d’un axe horizontale perpendiculaire à la tige passant par son centre O. Deux particules, chacune de masse 𝑚, sont fixées à la tige de part et d’autre de l’axe O, l’une à 𝐿 /2, et l’autre à 𝐿/ 4, de O. On écarte le pendule, ainsi constitué, de 𝜃𝑚 = 0.1 𝑟a𝑑 à partir de sa position d’équilibre et on l’abandonne sans vitesse initiale à l’instant 𝑡₀ = 0. Le pendule commence à osciller. Pendant le mouvement, à un instant t, il est à 𝜃 de sa position d’équilibre et il possède la vitesse angulaire 𝜃 ′ = 𝑑𝜃/ 𝑑𝑡. Le moment d’inertie de la tige par rapport à l’axe O est : J_O = 𝑀𝐿 ² /12. On donne :M=2Kg ; m=0.1 kg ; L=2m

1. Calculer le moment d’inertie du système ainsi constitué.

2. Déterminer l’expression de l’énergie mécanique du système, et établir l’équation différentielle du mouvement du centre de masse G du pendule.

3. Déterminer l’équation horaire du mouvement du système.

CORRIGES

EXERCICE I :

1. Ep=mgz=mgOG(1-cosθ) OG=L/2 et 1-cosθ≈θ²/2

2.=

^{Les frottements sont négligeables donc, Em est conservée.}

En dérivant les deux termes de l’expression par rapport au temps, on a :

)

//(cosu)’=u’sinu

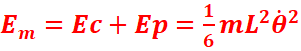
3.

=

EXERCICE II :

1.

a est la distance OG,

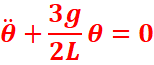
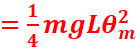
Pour des oscillations de faible amplitude, sinθ≈θ

=>

2.

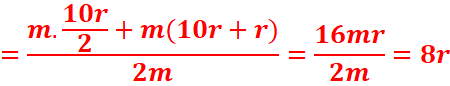
3,d=8r=20cm

.

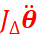
4. La solution de cette équation différentielle est de la forme Θ=θ_msin(ω₀t +φ)

A t=0, Θ=θ_m <=> θ_m =θ_msin(φ) => sin(φ)=1 => φ=π/2

Θ=10sin(6,32t + π/2) t en seconde et θ en radians

EXERCICE III :

1. J_Δ=J_O+m(L/4)² +m(L/2)²=ML²/12+mL²/16+mL²/4

=J_O+ml²/2= (4ML²+15mL²)/48

AN: J_Δ=(4x2+15x0,1)2²/48=0,79 kg.m².

2.Em=Ec + Epp=1/2 J +m’gL(1-cosθ)

= 1/2 J +m’ga

m’ est la masse totale de la tige + particules m’=M+m+m=2+0,1+0,1=2,2kg

En l’absence des frottements, Em est constant => dEm/dt=0

=>

C’est une équation différentielle de second ordre sans second membre de la forme : 

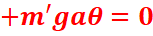
3.La solution de cette équation différentielle est de la forme Θ=θ_msin(ω₀t +φ)

A t=0, Θ=θ_m <=> θ_m =θ_msin(φ) => sin(φ)=1 => φ=π/2

Θ=0,1sin(0,79t + π/2) t en seconde et θ en radians