FORCES
GRAVITATIONNELLES
Un objet de
masse M exerce une force de gravitation attractive sur un autre objet de masse
m situé à une distance r telle que :

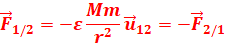
Où ![]() est un vecteur unitaire.
est un vecteur unitaire.
Loi d’attraction
universelle :
L’interaction
gravitationnelle entre deux corps A et B, de masses respectives M
et m, dont les centres de gravité sont séparés d’une distance r,
est modélisée par des forces d’attraction gravitationnelle et dont les
caractéristiques sont les suivantes :
- Point d’application : Le centre de
gravité qui subit la force.
- Direction : la droite (AB) passant par les centres de gravité.
- Sens : vers le centre attracteur.
- Intensité :
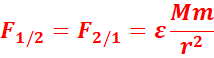
Les forces s’expriment en newton (N), les masses en kilogramme (kg) et la
distance r en mètre (m).
![]() est la constante universelle de gravitation et vaut :
est la constante universelle de gravitation et vaut :
![]() = 6,67.10-11 Nm2.kg-2
= 6,67.10-11 Nm2.kg-2
Champ de gravitation
On dit qu’il existe un champ de gravitation en un pont
de l’espace si une masse placée en ce point est soumise à une force de
gravitation.
Ce champ est caractérisé par un vecteur champ
gravitationnel noté![]() tel que :
tel que :
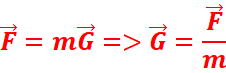
![]() en newton(N),
en newton(N),
m en kilogramme(Kg),
Le champ de gravitation ![]() s’exprime en newton par kilogramme (N.Kg-1)
s’exprime en newton par kilogramme (N.Kg-1)
Un cas particulier : le champ de pesanteur ou champ de gravitation
terrestre
L’interaction gravitationnelle que la terre
exerce sur un objet place en un point est pratiquement confondue avec le poids
de ce corps.
Le poids ![]() est donc la force de
gravitation que la terre exerce sur tous les objets qui l’entourent.
est donc la force de
gravitation que la terre exerce sur tous les objets qui l’entourent.
![]()
![]() en newton(N),
en newton(N),
m en kilogramme(Kg),
Le champ de gravitation ![]() s’exprime en newton par kilogramme (N.Kg-1)
s’exprime en newton par kilogramme (N.Kg-1)
NB : ![]() est aussi appelé accélération de la
pesanteur, elle s’exprime dans ce cas en mètre par seconde carre (m.s-2)
est aussi appelé accélération de la
pesanteur, elle s’exprime dans ce cas en mètre par seconde carre (m.s-2)
Variation du champ de pesanteur avec l’altitude
Un point A situé à une altitude h
au-dessus de la surface de la terre est à une distance r = RT + h du
centre de la terre.
L’intensité de la pesanteur (pratiquement
confondu avec le camp gravitationnel) au point A est :
![]()
En un point de la surface de
la terre, l’intensité de la pesanteur est :
![]()
Le rapport des deux
relations permet d’écrire :
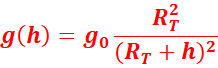
Sur la terre, g0~9,80
ms-2
Sur la lune, gL ~1,62ms-2
EXERCICES
EXERCICE
I :
On étudie la force exercée par la Terre sur la Lune.
1) Cette force est-elle : attractive ou répulsive ?
A distance ou de contact ?
2) Calcule la force gravitationnelle exercée par la
Terre sur la Lune.
3) Comment peut-on qualifier cette force ? (Sens,
direction, point d’application, intensité)
4) Schématise cette force sur un schéma sans
échelle.
5) La Lune exerce-t-elle une force sur la Terre ? Si
oui, schématise-la.
6) Peut-on parler d’interaction entre la Terre et le
Lune ?
EXERCICE II :
1.Quelle est la force
d’attraction universelle entre un proton et un électron distant de 10-10
m (atome d’hydrogène).
Masse du proton :
1,67x10-27 kg
Masse de
l’électron : 9,11x10-31 kg
2.a) Quelle est la force d’attraction entre la
lune et une personne qui se trouve sur la terre.
Masse de lune :
7,34x1022 kg
Masse de la
personne : 70 kg
Distance
Terre-Lune : 3,84x108 m
b) La personne se trouve dans un lieu ou g=10 N/kg, comparer cette force
a son poids.
EXERCICE
III :
La planète Terre est une sphère de diamètre D=12800km.
La lune est une planète de masse M=7,34x1022kg et de rayon
R=16,97x105m.
1.
Calculer
la masse de la terre sachant que l’intensité de la pesanteur au voisinage du
sol est g=9,78N/kg.
2.
Quelle
est l’intensité du champ de gravitation à la surface de la lune ?
3.
Quel
serait le poids d’un homme de masse 75kg à la surface de la lune.
EXERCICE
IV :
Deux
solides ponctuelles A et B de masses respectives mA=200kg et mB=500kg sont distants de 40 cm. Un troisième
solide C de masse mC=50kg est placé entre eux.
1.
Déterminer l’intensité de l’interaction gravitationnelle attribuable aux
solides A et B sur le solide C, lorsque ce dernier est placé au milieu du
segment AB.
2.
Quelle est la position de C pour que la force résultante soit nulle ?
EXERCICE V:
La valeur de la force
gravitationnelle exercée par le soleil sur Jupiter a pour valeur FS/J =
4,14.1023 N.
Données :
Ø Distance entre le soleil et Jupiter : d = 7,79.108 km
Ø Masse du soleil : mS
= 1,98.1030 kg
Ø Constante de gravitation universelle : 𝞮 = 6,67.10-11
SI
1. Calculer la masse mJ
de Jupiter
2. Que peut-on dire de la valeur
de la force FJ/S exercée par Jupiter sur le Soleil ?
3. Quelle relation vectorielle
existe-t-il entre ces deux forces ?
4. Représenter, sur le schéma
ci-dessous, ces deux forces en choisissant une échelle adaptée.
CORRIGES
EXERCICE I :
1) Force attractive et à distance
2) Soit mT, la masse de la terre et mL ,
la masse de la lune, FTL la force d’attraction.
𝐹𝑇𝐿 = 𝞮 × 𝑚𝑇×𝑚𝐿 /𝑑2𝑇𝐿
𝑑𝑇𝑒𝑟𝑟𝑒−𝐿𝑢𝑛𝑒 = 384 400 km = 384 400 000 𝑚 = 3,844 × 108𝑚
𝐹𝑇𝐿 = 6,67 × 10−11 × 5,972 × 1024× 7,3477×1022
(3,844 ×108)
𝐹𝑇𝐿 = 1,98 × 1020 𝑁
3) La force exercée par la Terre sur la Lune :
- Direction : sur la droite qui
passe par le centre de la Terre et le centre de la Lune
- Sens : de la Lune vers la Terre
- Point d’application : Le centre de la Lune
- Intensité : 𝐹𝑇𝐿 = 1,98 × 1020 𝑁
(calcul fait à la question 2)
4) En bleu, la réponse à la
question 4. En rouge, la réponse à la question 5.
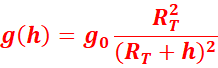
5) La Lune exerce aussi une force
sur la Terre. Elle aura la même direction et la même intensité que la force
exercée par la Terre sur la Lune. Le sens sera inversé (de la Terre vers la
Lune) et le point d’application sera le centre de la Terre.
6) La Terre agit sur la Lune et la Lune agit sur la Terre du fait de leur
masse. On parle d’interaction gravitationnelle.
EXERCICE II :
1.Calculons la force d’attraction
Soit m1, la masse du proton, m2, la masse de
l’électron
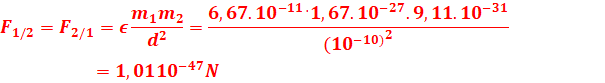
2. Soit mT la masse de la terre ,
mL la masse de la lune
![]()
b) P=mg=70x10=700N
P/F=700/2,32.10-3=308.103
La force est faible
devant le poids de la personne.
EXERCICE III :
1. Calcul
de la masse de la terre
![]()
Pour h=0, niveau de la mer,
![]() .
.![]()
2.A la surface de la lune,
![]() .
.
3. PL= mgL=75x1,7=127,5N
EXERCICE IV :
1. Intensité de l’interaction
gravitationnelle
r=d/2=20cm
![]() .
.
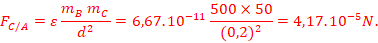
La résultante F= FC/B -
FC/A =4,17.10-5 -1,67.10-5=2,5N
2. Position de C pour que la force résultante
soit nulle
Soit x la distance AC
La distance CB sera d-x
![]()
![]()
La résultante F= FC/B -
FC/A
![]()
![]()
![]()
![]()
![]()
On trouve x=15,5 cm, la solution négative étant rejetée.
C doit être à 15,5 cm de A pour que la résultante soit nulle.
EXERCICE V :
1. Calcul de la masse mJ de
Jupiter
D’après la loi de gravitation universelle : FS/J = 𝞮 x mS
x mJ/ d 2
D’où : mJ
= F x d 2 /G x mS
A.N : mJ = 4,14.1023
x (7,79.1011) 2 /6,67.10-11 x 1,98.1030 =
1,90.1027 kg
2. La force exercée par Jupiter sur le Soleil a la même valeur que
la force exercée par le soleil sur Jupiter :
FJ/S = FS/J
3. Ces deux forces sont opposées : Elles possèdent la même valeur,
la même direction, mais ont des sens opposés :
FJ/S = - FS/J
4. Représentation des deux forces :
FJ/S = FS/J = 4,14.1023 N.
Echelle choisie : 1 cm pour
2.1023 N Soit : 4,14.1023 /2.1023 » 2,1 cm
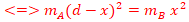
Avez-vous
un exercice à proposer ?Cliquez-ici
Merci de votre visite
Laissez un commentaire