CALCULS DANS IR

ENSEMBLE IR DES RÉELS
ℕ désigne l’ensemble des nombres entiers naturels exemple :0 ;1 ;2 …
ℤ désigne l’ensemble des nombres entiers relatifs : ce sont des nombres entiers naturels précédés ou pas
du signe + ou -. Exemples : -1000 ; -1 ; 0 ; 1 ; 14
𝔻 désigne l’ensemble des nombres décimaux. Un nombre décimal relatif est un nombre décimal précédé du signe moins ( ) ou du signe ( ). Lorsque le nombre est précédé du signe moins, il est dit négatif. Le nombre est positif lorsqu’il est précédé du signe plus.
ℚ désigne l’ensemble des nombres rationnels. Un nombre rationnel est un nombre pouvant se mettre sous
la forme où 𝑎 𝑒𝑡 𝑏 sont des nombres entiers relatifs.
Certains nombres ne sont pas des nombres rationnels ils sont dits irrationnels

Exemples : √2; √7; √27; 𝜋

L’ensemble ℝ des nombres réels est l’ensemble constitué des nombres rationnels et des nombres irrationnels.
Remarque : ℕ ⊂ ℤ ⊂ 𝔻 ⊂ ℚ ⊂ ℝ

FRACTIONS

Opérations sur les fractions

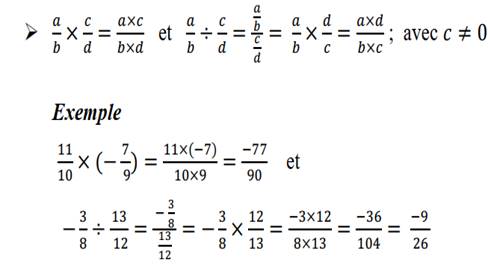
Propriété: Pour tout réels a, b, c et d avec b et d différents de zéro

a/b =c/d alors  ad=bc

Règles de priorités

Dans une suite d’opérations, l’ordre de priorité est le suivant :
- Les parenthèses : elles indiquent les calculs à effectuer en premier. On commence les calculs par ceux qui sont dans les parenthèses les plus intérieures.

-Les puissances.
-La multiplication et la division.
-L’addition et la soustraction.

PUISSANCE

v Soient a et b deux nombres réels, m et n deux nombres entiers. On a : 𝑎⁰ = 1 𝑎𝑣𝑒𝑐 𝑎 ≠ 0;

· 𝑎^𝑛 = 𝑎 × 𝑎 × 𝑎 × … × 𝑎 (𝑛 𝑓𝑎𝑐𝑡𝑒𝑢𝑟𝑠);

· 𝑎^-𝑛 = . ( ≠ 0).

· 𝑎^𝑛 × 𝑎^𝑚 = 𝑎 ^𝑛+𝑚;

· (𝑎^𝑛)^𝑚 = 𝑎 ^𝑛×𝑚 ;

· (𝑎 × 𝑏)^𝑛 = 𝑎^𝑛 × 𝑏^𝑛

· (-a)ⁿ=aⁿ si n est pair ou –aⁿ si n est impair

· ()ⁿ =

VALEUR ABSOLUE

Soit a un nombre réel quelconque, le plus grand des deux nombres réels –a et +a est appelé valeur absolue de a.

On note : │a│

On lit : « valeur absolue de a»

Exemples : │-7│=+7 et │+7│=+7

│Ѵ7. - 2│ =Ѵ7 -2

et │2-Ѵ7│=Ѵ7-2

Propriétés :

· │a│

· │a│=0 <=> a=0

· │a│=│-a│

· │a│= -a si a<0. ou a si a>0

· │a│=│b│ <=> a=b ou a=-b

· │axb│=│a│x│b│

· Si b est #0, │ │=

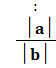
· Si b est #0, │ │=

· │a+b│ │a│+│a│

· │a│ -r a +r

NOTIONS D’INTERVALLES

Un intervalle est un ensemble de tous les nombres réels compris entre deux valeurs a et b appelées bornes de l’intervalle.

a et b pouvant être moins l’infini (←) ou plus infini (→)

Un intervalle s’écrit entre deux crochets.

Exemples :

· Intervalle ouverte :]a,b[

<= > a < x < b

· Intervalle fermée :[a,b]

<= > a≤x < b

· Intervalle semi-ouverte ou semi-fermée :

]a,b] < = > a <x ≤b

[a,b[ <= > a ≤ x < b

L’amplitude de l’intervalle est : (b-a)/2

RACINES CARRÉES

v Soient a et b deux nombres réels strictement positif. On a :

Ø

Ø

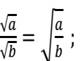
Ø

Ø

Ø

Ø

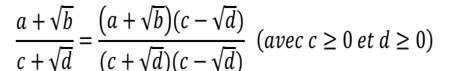
Remarque : généralement, pour tous nombres réels positifs 𝑎 𝑒𝑡 b ,

Ѵa+b ≠ √𝑎 + √𝑏

COMPARAISONS

Propriétés sur la Comparaison
P1 : Soient a , b et c des nombres rationnels,
𝑎 – 𝑏 = 0 signifie 𝑎 = 𝑏 ; 𝑎 – 𝑏 < 0 signifie 𝑎 < 𝑏 ; 𝑎 – 𝑏 > 0 signifie 𝑎 > 𝑏
𝑎 < 𝑏 signifie 𝑎 + 𝑐 < 𝑏 + 𝑐
Si 𝑎 < 𝑏 𝑒𝑡 𝑐 > 0 𝑎𝑙𝑜𝑟𝑠 𝑎 × 𝑐 < 𝑏 × 𝑐 ; 𝑆𝑖 𝑎 < 𝑏 𝑒𝑡 𝑐 < 0 𝑎𝑙𝑜𝑟𝑠 𝑎 × 𝑐 > 𝑏 × 𝑐

NOTIONS DE VALEUR APPROCHÉE

Soient x et y deux réels et l un réel positif,

y est la valeur approchée de x à l près signifie que la valeur │x-y│≤ l

On note : x ~ y à l près.

Le nombre l’ est appelé incertitude de cette valeur approchée.

Exemple : Faisons un encadrement de à 10^-3 près

On sait que : 1,166≤7/6≤,166

1,166 est la valeur approchée de 7/6 par défaut a 10^-3 près

1,167 est la valeur approchée de 7/6 par excès a 10^-3 près

Remarque :

La connaissance d’un encadrement de x permet de calculer sa valeur approchée.

Si x est compris entre a et b (a≤a≤b) alors (b+a)/2 est la valeur approchée de x à (b-a)/2 près.

Exemple : Calculer la valeur approchée de 7/6 à 10^-4 près sachant que 1,166≤x ≤1,167 à 10^-3 près

V_a =(1,166+1,167)/2 =1,1665 à (1,167-1,166)/2 = 0,0005 = 5.10^-4 près.

1,1665 est la valeur approchée de 7/6 à 10^-4 près

NOTATION SCIENTIFIQUE

Un nombre réel A est exprimé en notation scientifique lorsqu’il peut s’écrire sous la forme A=a.10^p

avec (a ϵ R et p ε Z) et 1≤│a│≤10

Exemple : 0,0005=5.10^-4

Remarque :

Lorsqu’on déplace la virgule vers la gauche l’exposant augmente : 9,3.10^-5=0,93.10^-4=0,093.10^-3…
Lorsqu’on déplace la virgule vers la droite l’exposant diminue : 0,093.10^-3=0,93.10^-4=9,3.10^-5….

EXERCICES

EXERCICE I :

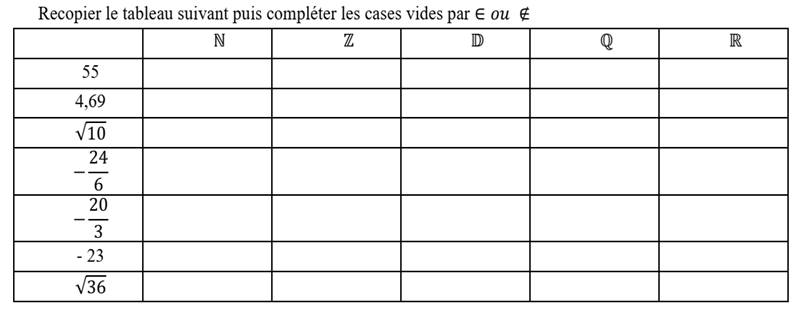
EXERCICE II :

EXERCICE III :

1. Ecrire sous la forme a+

R = (Ѵ3+Ѵ2)² - (Ѵ3-Ѵ2)²

S =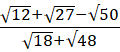

2. On pose A = +

Calculer A²

EXERCICE IV :

1. Calculer pour a=-3 ; b=10 et c=4 le nombre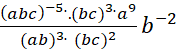

2. On pose : a=

b=

Calculer ab^-1

EXERCICE V :

On donne :

A= - . (a # 0 et a#-1)

B=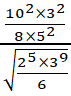

C=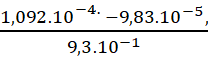

1-Ecrire A sous forme de quotient

2-Simplifier B et l’écrire sous forme de fraction irréductible

3-Donner l’écriture scientifique de C

4-Sachant que 2,645 ≤Ѵ7≤ 2,646

Donner un encadrement à 10^-4 près de (4-Ѵ7)/7

EXERCICE VI :

1.Ecrire sous forme d’intervalle

a) -5 ≤ x <7

b) 4≤x≤18

c) 3<x≤8

d) -12≤x<15

e) x>1

f) x< -33

2. Ecrire sous forme d’inégalité

a) x ∈[-2,1]

b) x ∈ ]4,8]

c) x

d) x ∈ [-6,1[

e) x ∈ [-6,→[

f) x ∈ ]←,1]

EXERCICE VII 

EXERCICE VIII :

1-Soit 3,144 ≤ x ≤ 3,145, Donner la valeur approchée de x à 10^-3 près.

2-Traduire par un encadrement chacun des informations suivantes :

a) 0,818 est une valeur approchée de 9/11 à 10^-3 près.

b) 2,351 est une valeur approchée de A à 2.10^-4 près

3-Exprimer en notation scientifique :

a). 16000x350

b).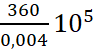

CORRIGES :

EXERCICE II :

1)

2)

3)

P=

4)

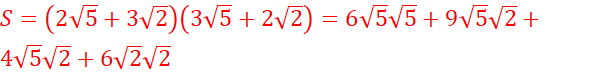
EXERCICE III:

1.

=

=

=

=4

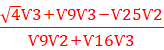
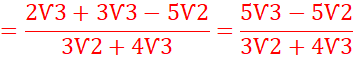
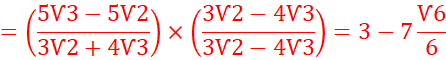
2.

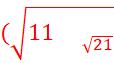
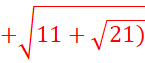
11 -

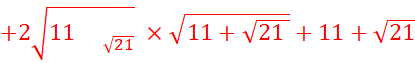
EXERCICE IV :

1.

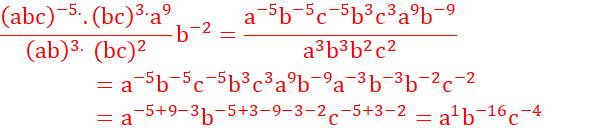
2.

. =

=

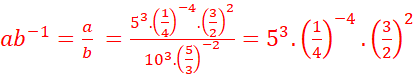EXERCICE V :

1. 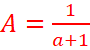- . = - = x= - ==

2.

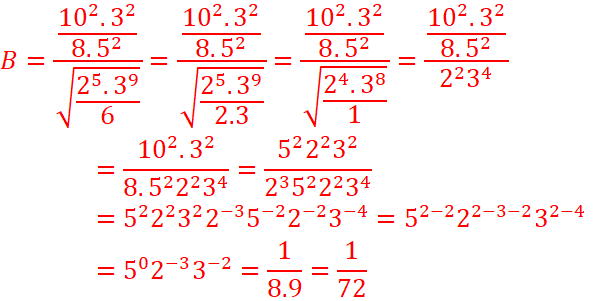
3.

..

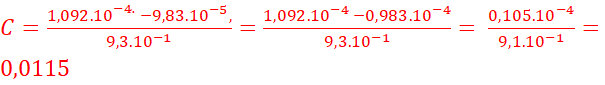4.

<=>

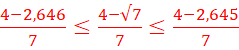
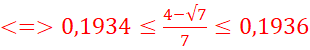
EXERCICE VI :

1.

a) -5 ≤ x <7 <= >x ∈ [-5,7[

b)4≤x≤18. <= >x ∈ [4,18]

c)3<x≤8. <= >x ∈ ]3,8]

d)-12<x<15 <= >x ∈ ]-12,15[

e) x>1<= >x ∈ ]1, →[

f) x< -33<= >x ∈ ]←,33[

2.

a) x ∈ [-2,1] <= > -2≤x≤1

b) x ∈ ]4,8]<= > 4<x≤8

c) x ∈ ]0,10[ <= > 0<x<10

d) x ∈ [-6,1[ <= > -6≤x<1

e) x ∈ [-6,→[ <= > x≥-6

f) x ∈ ]←,1] <= > x≤1

Avez-vous un exercice à proposer ?Cliquez-ici

Merci de votre visite
Laissez un commentaire