PENDULE SIMPLE
Description du pendule simple
Le pendule simple est formé par :
•
un fil inextensible de masse négligeable et de longueur l ;
•
une bille de masse m accrochée à l'extrémité du fil.
Etude dynamique du pendule simple
Si on écarte le pendule d'un angle θm
par rapport à la verticale et qu'on lâche le pendule, celui-ci se met à
osciller dans le plan vertical.

·
Le
référentiel du laboratoire est supposé galiléen ;
·
On
assimile la bille à un point matériel M qui ne subit que deux forces :
·
Bilan
des forces :
-le poids ![]()
-
la tension du fil ![]() .
.
Le
principe fondamental de la dynamique appliqué à la bille s’écrit :
![]()
Projetons
maintenant le Principe Fondamental de la Dynamique dans la base de Frenet ![]() :
:
![]()
![]()
car ![]()
![]()
![]()
![]()
![]()
L’équation
(1) nous permet d’écrire :
![]()
![]()
![]()
![]()
![]() (3)
(3)
C’est
l’équation différentielle d’un pendule simple non amorti. Ces solutions ne sont
pas sinusoïdales.
Pour des oscillations de faible amplitude
(θ < 0,026 rad), on peut écrire en première approximation sinθ ≈
θ en radian.
L’équation
différentielle devient alors :
![]()
On pose :
![]()
![]() (4)
(4)
Les
solutions sont de la forme :
Θ=θmsin(ω0t +φ)
Les
oscillations de faible amplitude d’un pendule simple sont donc sinusoïdales.
La
pulsation propre d’un pendule simple est :
![]()
Sa
période propre est :
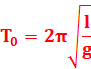
T0
en s
L
en m
g
en m.s-2
Etude énergétique du pendule simple
a) Energie mécanique de l’oscillateur
Lorsque le pendule oscille
d’une position extrême A vers sa position d’équilibre, l’énergie potentielle se
convertit en énergie cinétique et inversement. A chaque instant, on
a : Em = Ep +Ec
En
négligeant les frottements,
·
Au point A. point d’amplitude maximale :
Ep=mgz
Ec=0
(car v=0)
z=h=OC-OP=a(1-cosθ) =>
Ep=mga(1-cosθ)
Donc
Em(A)= Ep
On
suppose que le plan horizontal passant par C à l’équilibre, comme état de
référence de l’énergie potentielle de pesanteur, Ep = 0 en C.
·
Au point C, position d’équilibre :
Ep=0 (z=0
car C est le niveau de référence de l’énergie potentielle)
Ec=1/2
mv2
=> Em(C) = Ec
·
Pour une position M quelconque, Em=Ec + Ep =1/2
mv2 + mga(1- cosθ)
![]()
Cas des oscillations de
faible amplitude
Dans le cas des
oscillations de faible amplitude, cosθ≈1-θ2/2
![]()
//car cosθm≈1-θm2/2 =>1-cosθ≈θ2/2
![]()
![]()
// on remplace Θ par θmsin(ω0t
+φ) , ![]()
![]() et
et
![]()
![]()
![]()
![]()
//cos2x +sin2x=1
![]()
![]()
Conclusion : L’énergie mécanique d’un pendule simple
non amorti est donc constante.
Les
frottements sont négligeables donc, Em est conservée.
![]()
En
dérivant les deux termes de l’expression par rapport au temps, on a :
![]()
![]()
![]()
![]()
On retrouve l’équation déférentielle du mouvement du
pendule simple.
EXERCICES
EXERCICE
I :
Un pendule simple est constitué d’un fil de
longueur 50 cm, fixé, par l’une des extrémités, à un support et un solide (S)
de masse M=200 g, accroché à l’autre extrémité. On écarte le pendule de sa
position d’équilibre et on le lâche.
1.
Décrire le mouvement du pendule.
2.
Dans quel plan oscille le pendule ?
3.
Donner l’expression de la période des oscillations et la calculer
EXERCICE II :
On
écarte un pendule simple de masse m = 10g d’un angle Ѳm = 8° et
l’abandonne sans vitesse initiale. Il oscille librement. La longueur du pendule
est l = 0,8m et
g = 9,8 m.s-2. L’origine des
énergies potentielles est le plan horizontal contenant le solide suspendu à la
position d’équilibre.
1. Ecrire l’équation
différentielle du mouvement (faire le schéma).
2. Donner l’équation
horaire de l’abscisse angulaire Ѳ sachant qu’à t = 0, le pendule passe
par la position d’équilibre allant dans le sens des élongations décroissantes.
3. Calculer la période
propre T0 de l’oscillateur.
4. Calculer l’énergie
mécanique du système Terre-pendule.
5. Lorsque le pendule
passe par la position d’équilibre, le fil heurte sur une butée en un point A
tel que OA = 40cm. De quel angle Ѳ’m va-t-il s’élever de
l’autre côté ?
EXERCICE
III:
Un enfant se balance à l’aide d’une balançoire
constituée d’une barre qu’il utilise comme siège, suspendue par deux cordes
fixées à un support fixe. On modélise le système {enfant + balançoire} par un
pendule simple composé d’un fil, inextensible de masse négligeable et de
longueur L , et un corps (S) de masse m . Le système peut tourner autour d’un
axe fixe horizontal (Δ) perpendiculaire au plan vertical. Le moment
d’inertie du pendule par rapport à l’axe (Δ) est JΔ = m.L2
Données :
Intensité de la pesanteur : g = 9,8 m.s-2
; longueur du fil : L = 3 m ; masse du corps (S) : m = 18 kg. O prend
dans le cas de petites oscillations : sinθ ≈ θ et cosθ ≈
1 - θ2 /2 (rad). On néglige les dimensions du corps (S) par
rapport à la longueur du fil et tous les frottements.
1. Étude dynamique du pendule : On écarte le
pendule de sa position d’équilibre stable d’un angle θm= π /20 dans
le sens positif et le libère sans vitesse initiale à l’instant t = 0 . On
repère la position du pendule à un instant t par l’abscisse angulaire θ
défini entre le pendule et la verticale passant par le point O tel que θ =
(OMo,OM)

1-1-Montrer en utilisant la relation
fondamentale de la dynamique de rotation autour d’un axe fixe, que l’équation
différentielle du mouvement du pendule dans un référentiel galiléen lié à la
Terre s’écrit :
![]()
1-2-
Calculer la période propre To du pendule.
1-3-Écrire l’équation horaire du mouvement du
pendule.
1-4-
En appliquant la deuxième loi de Newton dans la base de Frenet, trouver
l’expression de la tension du fil T à un instant t en fonction de m, g, θ,
L et v la vitesse linéaire du pendule simple. Calculer la valeur de T à
l’instant t = To/ 4.
2Étude énergétique :
On fournit au pendule qui est immobile dans sa
position d’équilibre stable une énergie cinétique de valeur EC =
264,6 J, et il tourne dans le sens positif
2-1-On choisit le plan horizontal passant par
le point Mo comme référence de l’énergie potentielle de pesanteur (voire
figure). Écrire l’expression de l’énergie potentielle de pesanteur EP
du pendule à l’instant t en fonction de θ, m, L et g.
2-2-En
se basant sur l’étude énergétique, déterminer la valeur maximale θmax
de l’abscisse angulaire.
CORRIGES
EXERCICE I :
1. En vertu du principe
fondamental de la dynamique, on a :
![]() (1)
(1)
Dans la base de Frenet ![]() formée d’un
vecteur tangentiel
formée d’un
vecteur tangentiel ![]() dirigé dans le sens du mouvement et d’un
vecteur normal
dirigé dans le sens du mouvement et d’un
vecteur normal ![]() dirigé vers
le point de suspension du pendule, projetons le Principe Fondamental de la
Dynamique :
dirigé vers
le point de suspension du pendule, projetons le Principe Fondamental de la
Dynamique :
sur ![]() :
: ![]() (2)
(2)
sur ![]() :
: ![]() (3)
(3)
L’équation (3) nous permet
d’obtenir la tension du fil, tandis que l’équation (2) nous donne l’équation
différentielle du mouvement :
![]()
![]()
![]()
![]() (4)
(4)
Le terme en sinθ, rend
cette équation différentielle non linéaire
Pour de petites oscillations, on peut assimiler sin θ à θ
en radian. L’équation différentielle devient alors
![]()
On
pose :
![]()
![]() (4)
(4)
Les solutions sont de la forme :
θ=θmsin(ω0t +φ)
Les oscillations de faible amplitude d’un pendule simple sont donc
sinusoïdales.
2. Le pendule oscille dans le plan vertical.
3.La pulsation propre d’un pendule simple est : ![]()
Sa période propre est : 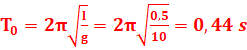
EXERCICE II :
1.
![]()
2. Θ=θmsin(ω0t +φ)
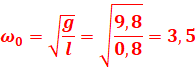
A t=0, Θ=0=θmsin(φ) => sin(φ) =0 => φ=0 ou φ=π
![]()
A t=0, ![]() => φ=π
=> φ=π
θ=8sin(3,5t +π)
θ=-8sin(3,5t)
3.
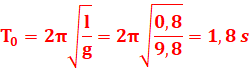
4. θₘ = 8° = 0,14 rad
![]()
5. Collision avec une butée à OA = 40 cm
Lorsque le pendule heurte la butée en A sa longueur effective devient
l’=0,8-0,04=0,76 m
L’énergie mécanique se conserve (on néglige les pertes).
A la position d’équilibre Em=Ec+Ep (Ep=0)
A la nouvelle position extrême, Em=Ep’=mgl’(1-cosθ’m)
Donc , mgl(1-cosθm)= mgl’(1-cosθ’m)
0,8(1-cos8)= 0,76(1-cosθ’m)
θ’m=8,2![]()
EXERCICE III
1-1
1-2
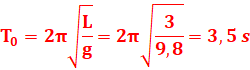
1-3. θ=θmsin(ω0t +φ)
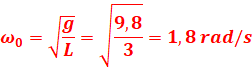
A t=0, Θ=θm=θmsin(φ) => sin(φ) =1 => φ=π/2
Θ=π/20sin(1,8t + π/2)
1-4 ![]()
![]()
![]()
![]()
![]()
![]()
Θ=π/20sin(1,8t + π/2)
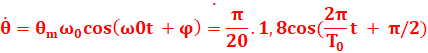
t = To/ 4
![]()
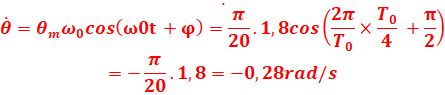
![]()
![]()
=18x9,8cos0 -18x3x(-0,28)2=176,4 - 4,23=172,2N
2.
2,1-Expression de l’énergie potentielle
Ep=mgL(1-cosθ)=1/2mgLθm2
2.2-En absence des frottements, il y a conservation de l’énergie
mécanique totale :
Em(M0)=Em(M)
<=>Ec=Ep
<=>![]()
