ACTION D’UNE INDUCTION MAGNETIQUE SUR UN COURANT

Loi de la place

F

N

S

Expérience : Deux tiges de cuivre constituent deux rails conducteurs sur lesquels peut rouler une barre cylindrique légère qui ferme le circuit. Un aimant en U crée une induction magnétique, perpendiculaire au plan horizontal.

Lorsqu’on fait passer un courant I dans le circuit, on constate que la barre se déplace.

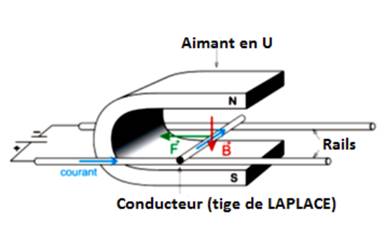
Interprétation : L’induction magnétique créée par l’aimant exerce sur l’élément de courant situé dans le champ une force , appelée force électromagnétique.

Enoncé de la loi de Laplace :

Un conducteur rectiligne de longueur parcouru par un courant d’intensité i, placé dans un champ magnétique uniforme d’intensité B, est soumis à une force électromagnétique dite force de Laplace.

Caractéristique de  :

· Point d’application : milieu du conducteur.

· Direction : Elle est perpendiculaire au plan formé par le conducteur et l’induction.

· Sens Donnée par la règle de la main droite.

· Son intensité :

= i ∧ ,

Règle des trois doigts de la main droite :

Application :

- Moteur électrique

- Roue de Barlow

- Balance de Cotton

Travail des forces électromagnétiques 

Notion de flux

I

Soit un élément de circuit fermé placé dans un champ magnétique uniforme .le flux d’induction coupee par un element de courant est, par definition, le produit de la surface S que balaie l’élément de courant par la composante Bcosθ, du vecteur induction normale a cette surface.

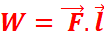
Ø = BSCos (, ) = BSCos𝜃

Unité du flux: le weber (Wb)

S en m² et B en T

Remarque :

Si 𝜃 = O ↣ Ø = BC

Si 𝜃 = ↣ Ø = 0

Si 𝜃 = ↣ Ø = BS

Le flux est une valeur algébrique

Travail des forces électromagnétique

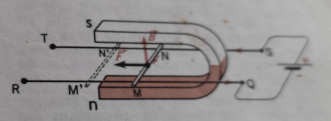
Le travail exercé par la force pour se déplacer de M à M’ est W = F.MM’

Or d’après la loi de Laplace : F = BIl

W = BIl.MM’ = BI.MN.MM’ = BIS

W = BIS

Cas où n’est plus perpendiculaire au plan des rails.

W = BIS cos𝜃

𝜃 = angle de l’induction

B et de la normale au plan des rails

Ø : Flux d’induction coupé ou balayé par un élément du circuit qui se déplace.

- En fonction du flux coupé sachant que Ø = BS Cos 𝜃

On a : W = ØI

En fonction de la variation du flux : W = I (Ø₂ – Ø₁)

Loi de Maxwell : Lorsqu’un circuit se déplace dans un champ magnétique, le travail des forces électromagnétiques qui s’exercent sur lui est égal au produit de l’intensité du courant par la variation du flux d’induction qui le traverse

ΔØ > 0 travail moteur

ΔØ < 0 travail résistant

Règle du flux maximal :

Un circuit plan parcouru par un courant et libre de se mouvoir, placé dans un champ magnétique est en équilibre stable quand le flux qui le traverse est maximal.

Les électro-aimants

On appelle électro-aimant tout dispositif comprenant du fer autour duquel s’enroule des spires conductrices où l’on peut faire passer un courant électrique. Un électro-aimant est un aimant temporaire. On appelle force portante d’un électro-aimant la force qu’on doit exercer sur l’armature pour la séparer du noyau.

Application : Des objets lourds 

Le galvanomètre

Un galvanomètre a cadre mobile est un appareil utilisant l’action d’un champ magnétique sur un courant pour mesurer ou seulement déceler des courants de faible intensité.

a- Le courant passe dans un cadre, c.-à-d. dans une bobine rectangulaire comprenant quelques centaines de spires d’un fil en cuire recouvert de vernis isolant.

b- Le champ magnétique agissant sur le courant qui parcourt le cadre est créé par un aimant en U muni de deux pièces polaires de fer doux.

Si le cadre comprend N spires identiques, l’ensemble des N couples équivaut à un couple électromagnétique de moment M=INBS. Ce couple électromagnétique fait tourner le cadre. Il en résulte une torsion des fils de suspension dont le moment a pour expression M’=Cα, C étant la constante de torsion.

De l’égalité de ces deux moments, on l’expression de la déviation α qui correspond au courant d’intensité I.

M=M’ <= >Cα=INBS =>

Un galvanomètre est d’autant plus sensible qu’a une déviation α donnée correspond une intensité I plus faible.

On mesure la déviation du cadre par la méthode de Poggendorff, fondé sur le fait que lorsqu’un miroir tourne d’un angle 𝜶, le rayon réfléchi tourne d’un angle 2𝜶 dans le même sens.

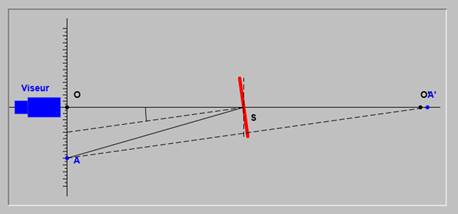
Un miroir plan parallèle à l'axe de rotation est fixé sur le dispositif dont on veut mesurer la rotation.
Un viseur permet d'observer l'image d'une règle graduée donnée par le miroir. Si l'équipage mobile est au repos le dispositif est réglé pour que le zéro de la graduation (point O) donne une image O'.
Quand le miroir tourne, l'observateur voit défiler dans le viseur l'image A' des graduations A de la règle. Si la frontale du viseur est suffisante, l'image des graduations reste nette.
Si le miroir tourne de l'angle α le rayon SO réfléchi par le miroir est fixe. Le rayon incident AS fait un angle 2α avec SO.

On pose OA=d et OS=D, alors :

.

EXERCICES

EXERCICE I :

Un conducteur rectiligne de 0,4m de longueur et parcouru par un courant constant d’intensité 12A est placé dans un espace où règne un champ magnétique uniforme 𝐵⃗⃗⃗ de valeur B=0,25T. Déterminer la valeur de la force magnétique qui s’exerce sur le conducteur quand il fait avec les lignes de champ un angle de 30° puis de 45°.

EXERCICE II :
Un conducteur rectiligne de 0,4m de longueur et parcouru par un courant constant d’intensité 12A est placé dans un espace où règne un champ magnétique uniforme d’intensité 0,25T. On constate que le conducteur se déplace.

1. Identifier la force qui fait déplacer le conducteur.

2. Calculer l’intensité de cette force.

a) Lorsque le conducteur est perpendiculaire au vecteur champ magnétique.

b) Déterminer la valeur de la force magnétique qui s’exerce sur le conducteur quand il fait avec les lignes de champ un angle de 30°.

EXERCICE III :

Les électrons pénètrent dans un champ magnétique perpendiculaire avec une vitesse.

1. Identifier la force qui agit sur cet électron.

2. Calculer l’intensité de la force de Lorentz lorsque v=2.10⁵ m.s^-1 et B=200 mT.

3. Comparer intensité de cette force au poids de l’électron sur terre.

EXERCICE IV :

Les deux tiges des rails de la figure ci-dessous sont écartées de 20 cm et la barre cylindrique MN leur est perpendiculaire. Le tout est dans un champ uniforme dont l’induction est normal au plan des rails et a pour intensité B=0,5 T. Les extrémités Q et S sont reliées aux bornes d’un générateur de fem E=6V et la résistance totale du circuit ainsi réalisé est R=2 Ώ.

1. Calculer l’intensité de la force électromagnétique qui s’exerce sur MN.

2. Calculer le travail que cette force effectue au cours d’un déplacement MM’=10 cm

EXERCICE V :

1.La sensibilité d’un galvanomètre est de 0,5 x 10³ rad/A. le galvanomètre est formé d’un cadre carré de 5 cm de côté et comporte 200 spires. La constante de torsion du fil de suspension est C = 4.10^-8 Nm/rad. Déduire de ces données la valeur moyenne du champ magnétique dans l’entrefer de l’aimant.

2.La sensibilité d’un galvanomètre est de T = 5.10⁴ rad/A. Quelle est la plus petite intensité décelable par cet appareil lorsqu’on mesure la déviation d’un spot sur une règle graduée en millimètres et placé à un mètre du galvanomètre ?

CORRIGES

EXERCICE I :

L'expression de la force de Laplace est 𝐹 =I𝑙 L𝐵⃗

En norme, on a F=IlBsin(I𝑙 ,𝐵⃗ )=IlBsina

A.N. Si a=30° F=0.6N Si a=45° F=0.86N

EXERCICE II :

2.Ʌ

< => F=qvBsin90=evB=1,6.10^-19.2.10⁵.200.10^-3=640.10^-17 C

3. =.

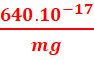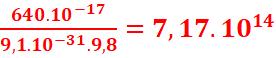EXERCICE III :

L'expression de la force de Laplace est

En norme, on a F=IlBsin(I𝑙,𝐵⃗ )=IlBsina
A.N. Si a=30° F=0.6N
Si a=45° F=0.86N

EXERCICE IV :

1.

F=IlBsinα =E/RrlBsin90 =.0,2.0,5.1 =0,3 N.

2.

=> W=F.l=0,3x0,1=0,03J.

EXERCICE V:

2.Pour mesurer l’angle de déviation du cadre, on utilise la méthode de Poggendorff, fondé sur le fait que lorsqu’un miroir tourne d’un angle 𝜶, le rayon réfléchi tourne d’un angle 2𝜶 dans le même sens.

d: Déplacement du spot

D: Distance miroir règle.

⇒I=10^-3/2x1x5x10⁴=10^-8A

Avez-vous un exercice à proposer ? Cliquez-ici