PENDULE DE TORSION

Description du pendule de torsion

Un pendule de torsion est composé d’un solide suspendu a un fil de torsion dont l’extrémité supérieure est fixée à un support. Lorsqu’on tourne le solide d’un angle θ. Le fil tordu exerce un couple de rappel : le couple de torsion, qui tend à ramener le solide a sa position d’équilibre, Le pendule ainsi forme effectue alors des oscillations.

Etude dynamique du pendule de torsion

On étudie le mouvement du système dans un référentielle terrestre supposé Galiléen.

On repère les positions de la tige à chaque instant par l’abscisse angulaire θ(t) mesuré à partir de la direction de la tige à l’équilibre. (Direction de référence)

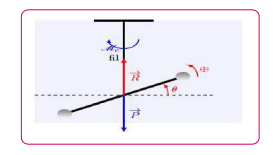
La tige est soumise à des forces suivantes :

* le poids :

* la réaction exercée par le fil :

Le moment du couple de torsion qu’exerce un fil tordu est indépendant de l’axe de rotation, il a pour expression : M_C=−C.θ

On applique la relation fondamentale de la dynamique de rotation au système :

+ +

Les droites d’action de et sont confondues avec l’axe, donc :

La relation devient :

C’est l’équation différentielle du mouvement du pendule.

C : la constante de torsion du fil (N.m/rad)

θ : angle de torsion (rad)

On pose :

L’expression devient :

C’est une équation différentielle de second ordre sans second membre, la solution est de la forme :

Θ=θ_msin(ω₀t +φ)

Remarques :

* Le signe négatif signifie que le couple de torsion est un couple de rappel ;

* La constante de torsion du fil dépend de la longueur du fil, de la section et de sa nature.

· Sa pulsation propre est :

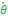
· La fréquence propre de l’oscillateur est :

· Sa période propre est :

Etude énergétique du pendule de torsion

a) Energie mécanique de l’oscillateur

Lorsque le pendule de torsion oscille, l’énergie mécanique apparait sous deux formes :

Energie potentielle élastique de torsion :

Energie cinétique du solide en rotation :

En prenant comme niveau de référence de l’énergie potentielle de pesanteur le plan horizontal contenant le centre d’inertie du pendule, celle-ci est nulle pendant le mouvement. En l’absence des forces dissipatives l’énergie mécanique du système est :

//On remplace Θ par θ_msin(ω₀t +φ) et par ω₀θ_mcos(ω₀t +φ)

On sait que : //car

//car sin²x +cos²x=1

et donc

L’énergie mécanique d’un pendule de torsion non amorti reste constante au cours des oscillations. Elle est proportionnelle au carré de l’amplitude.

b) Etablissement de l’équation différentielle à partir de la conservation de l’énergie mécanique totale

On peut retrouver l’équation différentielle du mouvement à partir de l’énergie mécanique

En l’absence des frottements. Il y a conservation de l’énergie mécanique totale.

Em =constante =>

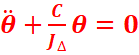
On retrouve l’équation déférentielle du mouvement du pendule de torsion.

EXERCICES

EXERCICE I :

Une barre est suspendue en son milieu a un fil de torsion verticale de constante de torsion (C). En exerçant perpendiculairement à la barre, à une extrémité de la barre mesurant 10 cm , une force horizontale de 0,16 N, on fait effectuer au système, une rotation de 45.

1.Calculer la constante de torsion du fil.

2.Calculer l’énergie potentielle du système fil-barre.

3.A cette position, on abandonne le système sans vitesse initiale. On prendra pour origine l’instant ou l’angle de rotation est maximal.

On donne J=0,01 kg.m². Les frottements sont négligeables.

a-Montrer qu’il effectue un mouvement oscillatoire.

b-Ecrire l’équation de ce mouvement

EXERCICE II :

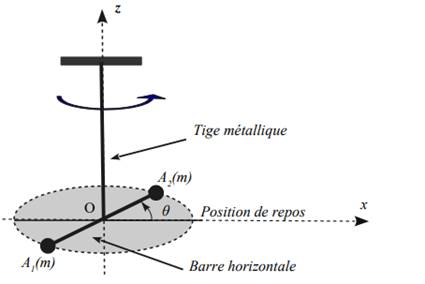
Le pendule de torsion est constitué par une barre horizontale de longueur 2d suspendue en son centre O à l'extrémité inférieure d'un fil métallique dont l'extrémité supérieure est reliée à un support fixe. La barre peut tourner autour de l'axe Oz vertical ascendant matérialisé par le fil. Le fil métallique exerce sur la barre une action mécanique de rappel dont le moment par rapport à l'axe Oz est ΓOz=−Cθ où θ est l'angle que fait la barre par rapport à sa position d'équilibre et C la constante de torsion du fil. Aux extrémités de la barre horizontale repérées par les points A1 et A2 sont fixées deux masse m identiques.

On note J =2 md² le moment d'inertie du système (S) constitué par la barre horizontale et les deux masses m par rapport à l'axe Oz. Le référentiel terrestre de repère d'espace R(O ,u⃗x , u⃗y ,u⃗z ) est considéré comme galiléen. On écarte légèrement la barre d'un angle θ₀ par rapport à sa position d'équilibre et on la lâche sans vitesse initiale. Le système se met à osciller sans frottement à la période T₀ autour de l'axe (Oz).

1. Justifier l'expression du moment d'inertie du système (S).

2. En appliquant le théorème du moment cinétique par rapport à l'axe (Oz) au système (S), établir l'équation différentielle du mouvement en θ du système (S) puis la résoudre.

3. En déduire la constante de torsion (C ) du fil de torsion en fonction de m, d et T0.

4. A partir de l'équation différentielle du mouvement établir l'intégrale première de l'énergie, en déduire l'énergie potentielle dont dérivent les actions de rappel.

EXERCICE III :

On dispose d'un pendule de torsion (P) formé de :

· Une tige homogène et uniforme AB suspendue en son centre de masse O à un fil de torsion vertical, dont l'extrémité supérieure est fixée en un point O' ;

· Deux objets identiques (S1) et (S2), assimilés à des particules, de même masse m = 200 g. Ces deux particules sont fixées sur la tige à la même distance réglable « x » de part et d'autre de O. (Doc. 1) Le fil de torsion OO', de masse négligeable, a une constante de torsion( C) et la tige AB possède un moment d'inertie I₀ par rapport à un axe (D) confondu avec (OO').

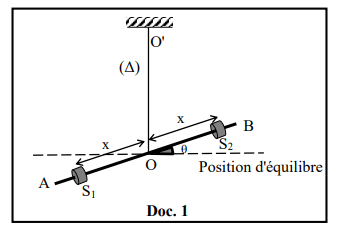
On écarte la tige de sa position d'équilibre d'un angle qm dans le plan horizontal puis on la lâche sans vitesse initiale. La tige se met à osciller, sans frottement, dans un plan horizontal autour de (D). À la date t, l'abscisse angulaire de la tige est q et sa vitesse angulaire est q' = dt /dq . Le plan horizontal contenant la tige est pris comme niveau de référence de l'énergie potentielle de pesanteur. Prendre p² = 10