STATISTIQUES

GENERALITES

Rangement en classe

Pour réaliser l’étude statistique d’un caractère quantitatif pouvant prendre toutes les valeurs sur un intervalle, on regroupe parfois ces valeurs en classe.

Effectif d’une classe

 L’effectif d’une classe est le nombre d’individus dont les modalités appartiennent à cette classe.

Exemple : On a regroupé dans le tableau ci-dessous le nombre d’avocatiers d’une pépinière en fonction de leur taille en cm. La série statistique obtenue est regroupée en classes.

30 avocatiers ont une taille comprise entre 0 et 5 cm

12 avocatiers ont une taille comprise entre 10 et 15 cm

…

Amplitude

 · L’amplitude d’une classe [a,b[ est le nombre b-a

Pour la classe [ 10,15[,

L’amplitude est 15-10=5

Centre

· Le centre est le nombre (a+b) /2

Exemple : le centre la classe [10,15[ est (10+15) /2=12,5

Densité d’une classe

C’est le quotient de l’effectif par l’amplitude de la classe.

Fréquence

 La fréquence en pourcentage d’une classe est donnée par la formule :

 Fréquence de la classe [ a,b[ est :

Exemple : la fréquence de la classe [5,10 [   est :

 Remarque : la somme de toutes les fréquences en pourcentage est toujours égale à 100.

Effectifs et fréquences cumulés

-On appelle effectif cumulé croissant (ECC) d’une modalité le nombre d’individu dont l’effectif est inférieur ou égal à cette modalité.

-On appelle effectif cumulé décroissant (ECD) d’une modalité le nombre d’individu dont l’effectif est supérieur ou égal à cette modalité.

-On appelle fréquence cumulé décroissant (FCC) d’une modalité le rapport de ECC par l’effectif total.

 

Quartiles, écart interquartile

Le premier quartile est la plus petite valeur de la série telle qu'au moins 25 % des autres valeurs de la série sont inférieures ou égales à cette valeur. Le troisième quartile est la plus petite valeur de la série telle qu'au moins 75 % des autres valeurs de la série sont inférieures ou égales à cette valeur.
L'écart interquartile d'une série statistique de premier quartile Q1 et de troisième quartile Q3 est égal à la différence Q3 - Q1.

 

Remarque :

 L'écart interquartile d'une série mesure la dispersion autour de la médiane. Il contient au moins 50% des valeurs de la série. L'écart interquartile n'est pas influencé par les valeurs extrêmes de la série.

 

CARACTERISTIQUES DE POSITION

Classe modale et mode

·         La classe modale est la classe ayant le plus grand effectif.

·         Le mode est le centre de la classe modale.

Exemple : Dans l’exemple ci-dessus, la classe modale est [5 ; 10[.

                                                             Le mode est (5 + 10)/2.

NB: Étant donné que les modalités sont des variables discrètes, les modes et les classes modales seront définis à partir des effectifs et non des densités.

 

Moyenne :

La moyenne d’une série statistique est le réel :

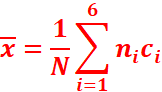
 , où ni est l’effectif de centre ci.

Médiane

            On appelle médiane d’une série statistique la modalité qui correspond à la moitié de l’effectif total. La classe médiane est la classe qui contient la médiane.si N est l’effectif totale, la médiane Me est telle que le nombre d’individus de modalité supérieur a Me et le nombre d’individus de modalité inférieur à Me soit N/2.

 

Détermination d’une médiane par interpolation linéaire :

Me  étant la médiane, N/2 la moitié de l’effectif, soit le point M(Me,N/2) compris entre les points A(xA,yA) et le point B(xB,yB), la médiane est donnée par la relation :

 

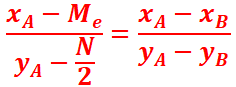
Exemple : soit la série statistique suivante :

classes

[2,5[

[4,6[

[6,8[

[8,10[

Total

Effectif

7

9

21

13

50

ECC

7

16

37

50

 

 

La moitié de l’effectif est N/2=25

25 est compris entre les classes [4,6 [  et   [6,8[, donc Me est compris entre 6 et 8.

6           →      16

Me        →       25

8           →       37

Par interpolation linéaire :

  =>Me=6,3

 

CARACTERISTIQUES DE DISPERSION

Variance

La variance d’une série statistique est le réel positif :

.

 

La formule de KEONIG :

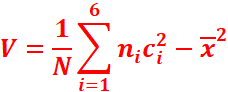
 permet de calculer plus facilement la variance.

Ecart-type

L’écart type d’une série statistique est le réel positif :

 

Ecart moyen

 L’écart moyen d’une série statistique est le réel positif :

 

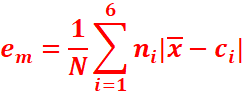
L’écart-moyen permet de mesurer la dispersion d’une série.

Intervalle moyen

 L’intervalle est appelé intervalle moyen. Le pourcentage d’observations contenues dans cet intervalle donne une mesure de la concentration des observations autour de la moyenne.

Exemple : soit la série statistique suivante :

Classe

[ 0,5[

[ 5,7[

[ 7,9[

[ 9,15[

Total

Effectif

15

78

36

21

150

ECC

15

93

129

150

 

ECD

150

135

57

21

 

Fréquence

10

52

24

14

100

Centre :ci

2,5

6

8

12

 

nici

37,5

468

288

252

1045,5

ni(ci)2

93,75

28,08

23,04

3024

8229,75

 

Moyenne :

Variance :

Ecart-type :

 

REPRESENTATION GRAPHIQUE

Histogramme

 Un histogramme d’une série statistique est un graphique composé de rectangles juxtaposés dont les bases sont les amplitudes des classes et les hauteurs sont proportionnelles aux densités de ces classes.

 

Cas des classes de même amplitude

Ø  Si les classes ont toutes la même amplitude, alors la hauteur d’un rectangle est proportionnelle à l’effectif (ou à la fréquence) de la classe qu’elle représente.

Exemple : Construisons l’historique de la série ci-dessous 

 

:

Cas des classes d’amplitudes différentes

 

Ø  Si les classes ont des amplitudes différentes, alors la hauteur d’un rectangle est proportionnelle à la densité de la classe qu’elle représente, la classe modale ici est celle qui a la plus forte densité.

·         La largeur de chaque rectangle est proportionnelle à l’amplitude de la classe qu’elle représente, on choisira de multiplier ou diviser l’amplitude par le nombre qui convient pour obtenir une mesure que l’on peut construire.

·         Les aires des rectangles doivent être proportionnelles aux effectifs des classes, on calculera dont les aires des rectangles à partir des effectifs et d’un coefficient de proportionnalité que l’on choisit à sa convenance.

·         On déduit les hauteurs des rectangles en divisant les aires par les largeurs.

 

Dépenses

[0,500[

[500,750[

[750,1000[

[1000,1500[

[1500,3000[

Effectifs

440

320

400

480

300

Amplitude

500

250

250

500

1500

Largeur

2

1

1

2

6

Aire

11

8

10

12

9

Hauteur

5,5

8

10

6

1,5

 

Polygone des effectifs

            Le polygone des effectifs est une ligne brisée obtenue en joignant les milieux des segments supérieurs de chaque rectangle de l’histogramme.

 Le polygone des effectifs cumulés croissants (resp décroissants) est une ligne brisée joignant les points ayant pour abscisse la borne supérieure ( esp la borne inférieure ) de la classe et pour ordonnée l’effectif cumulé de la classe.

               

Construction des EEC :

1-Placer en ordonnées les EEC.

- Placer en abscisse les valeurs supérieures des classes. Pour éviter de mettre tous les éléments, on place souvent un double trait signifiant que l’on coupe l’axe.

2.On place les points du tableau, ensuite on relie ces points.

NB : les ECD sont des nombres qui sont de plus en plus petits, on prend les valeurs inferieures des classes.

Exemple : Soit la distribution suivante :

xi

[0,5[

[5,7[

[7,10[

[10,12[

[12,14[

[14,16[

total

ni

6

8

10

3

1

1

29

 

Pour construire les polygones des ECC et ECD, on complète le tableau

xi

[0,5[

[5,7[

[7,10[

[10,12[

[12,14[

[14,16[

total

ni

6

8

10

3

1

1

29

ECC

6

14

24

27

28

29

 

ECD

29

23

15

5

2

1

 

 

                       

 

Dans un repère cartésien, on place les ECC (ou ECD) en ordonnées et les classes e abscisses

 

 

 

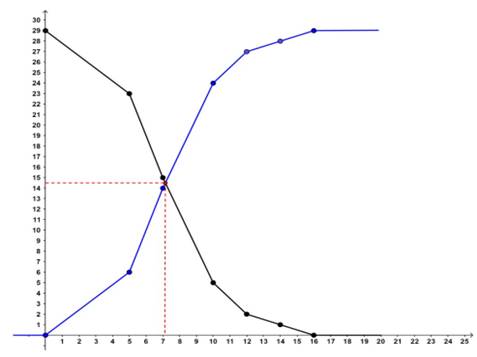
  A l’aide du polygone des ECC (en bleu) où des ECD (en noir), on détermine la médiane d’une série statistique. En effet la médiane est l’abscisse du point de l’effectif cumulé croissant où décroissant dont l’ordonnée est la moitié de l’effectif total N/ 2.

 

 

EXERCICES

EXERCICE I: Une enquête a été réalisée et a donné les tailles exprimées en cm de 51 élèves d’une classe.

1.Completer le tableau

Classes

[150,160[

[160,165[

[165,170[

[170,178[

total

Effectif

12

20

11

8

51

ECC

 

 

 

 

 

ECD

 

 

 

 

 

 

2. Déduire le nombre d’élèves qui ont une taille inférieure à 165

3. Déduire le nombre d’élèves qui ont une taille supérieure ou égal à 160

4. Déterminer moyenne, la variance, l’écart-type et la médiane de cette série statistique.

 

EXERCICE II: soit la série statistique suivante :

classes

[0,4[

[4,8[

[8,12[

[12,14[

14,16[

[16,20[

total

Effectif

38

50

32

24

26

30

200

 

1.Completer

classes

[0,4[

[4,8[

[8,12[

[12,14[

14,16[

[16,20[

total

Effectif

38

50

32

24

26

30

200

ECC

 

 

 

 

 

 

 

ECD

 

 

 

 

 

 

 

 

2.Calculer la moyenne, variance et l’écart-type

3.Construire les polygones des ECC et ECD

4.En déduire la médiane par la méthode graphique.

 

CORRIGES

EXERCICE I:

Classes

[150,160[

[160,165[

[165,170[

[170,178[

total

Effectif

12

20

11

8

51

ECC

12

32

43

51

 

ECD

51

39

19

8

 

ci

155

162,5

167,5

174

 

nici

1860

3250

1842,5

1392

8344,5

ni(ci)2

288300

528125

308618,75

242208

1367251,75

 

2.   32 représente le nombre d’élèves qui ont une taille inférieure à 165 cm

3.   39 représente le nombre d’élèves qui ont une taille supérieure ou égal à 160 cm

4. 

Moyenne= :

 Variance :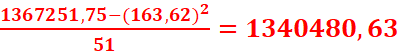

 L’écart-type :

  La médiane :

La moitié de l’effectif est N/2=25,5

25,5 est compris entre les classes [150,160[et   [160,165[ donc Me est compris entre 6 et 8.

160           →      12

Me        →       25,5

165       →       32

Par interpolation linéaire :

  =>Me=156,63

 

EXERCICE II :

classes

[0,4[

[4,8[

[8,12[

[12,14[

14,16[

[16,20[

total

Effectif

38

50

32

24

26

30

200

ECC

33

88

120

144

170

200

 

ECD

200

162

112

80

56

30

 

ci

2

6

10

13

15

18

 

nici

76

300

320

312

390

540

1938

ni(ci)2

152

1800

3200

1656

5850

9720

22378

 

2.

Moyenne :

 Variance :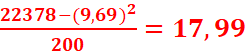

 L’écart-type :

3.  ECC en rouge et ECD en noir.

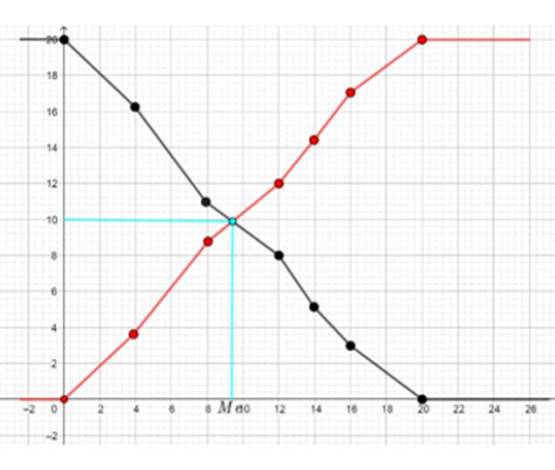
L’abscisse du point de rencontre des deux polygones est la médiane de la série statistique.

Me = 9,5

On peut verifier par le calcul :

La moitié de l’effectif est N/2=100

25,5 est compris entre les classes [4,8[  et   [8,12[ donc Me est compris entre 8 et 12.

8          →      88

Me        →       100

12      →       120

Par interpolation linéaire :

  =>Me=9,5