PENDULE ELASTIQUE

Description

Un pendule élastique, ou système solide-ressort, est constitué d'un solide, de masse m , fixé à un ressort ,de longueur initiale ℓ₀ et de raideur K, dont l'autre extrémité est attachée à un point fixe.

Le solide, écarté de sa position initiale, puis abandonné à lui-même, effectue un mouvement oscillatoire linéaire autour de sa position d’équilibre. Le système solide-ressort constitue un oscillateur mécanique encore appelé pendule élastique (horizontal dans ce cas).

On distingue :

-le pendule élastique horizontal

-le pendule élastique vertical

-le pendule élastique oblique.

Cas du pendule élastique horizontal

Sur un plan lisse on attache à l’extrémité d’un ressort de spires non jointives et de masse négligeable, un corps (S) de masse m, on l’écarte de sa position d’équilibre, et on le lâche sans vitesse initiale, le solide effectue donc un mouvement rectiligne oscillatoire.

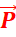
Equation déférentielle du mouvement

Étudions ce système dynamiquement :

Le système étudié : (S)

Bilan des forces :

: Le poids du corps

: La réaction du plan

: La tension du ressort

Dans le référentiel terrestre supposée galiléen on associe le repère (Ox), On applique la deuxième loi de Newton :

Projectons cette relation sur l’axe des x

Donc

On pose :

L’équation devient :

C’est une équation différentielle linéaire du second ordre car elle relie la variable x et sa dérivée seconde.

Sa solution s’écrit sous forme :

x_m est l’amplitude maximale en mètres(m)

ω₀ est la pulsation en radian par seconde(rad.s-1)

φ est la phase a l’origine en radian(rad)

x_m, w₀ et φ sont des constantes caractéristiques du mouvement.

Pulsation, amplitude et phase initiale

· Sa pulsation propre est :

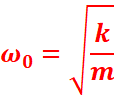
k en newton (N)

m en kilogramme (k)g

w₀ en radians par seconde(rad.s^-1)

· La fréquence propre de l’oscillateur est :

soit

· Sa période propre est :

soit

ne dépendent que des paramètres caractérisant l’oscillateur (la masse m et la constante de raideur k) : c’est pourquoi ces grandeurs sont dites propres. Tout oscillateur possède une fréquence propre et une période propre.

· L’amplitude x_m des oscillations et la phase initiale φ sont déterminées à partir des conditions initiales.

Cas du pendule élastique vertical

À l’extrémité libre d’un ressort de spires non jointives et de masse négligeable, on attache un corps (S) de masse m, le ressort s’allonge d’une distance ∆l₀.

Pour la déterminer on étudie le système en équilibre :

A l’equilibre,

avec

Lorsqu’on ecarte la masse de sa position d’equilibre, la tension du ressort a un instant donnee est differente de sa valeur a l’equilibre :

avec

En allongeant le corps (S) vers le bas, il effectue un mouvement oscillatoire, on suppose que l’air n’a aucun effet sur le mouvement de (S) :

d’apres le TCI :

P - T= ma <=>mg -T=ma

<=>mg – [kx +k(leq-l₀)]=ma

<=>mg – kx - k(leq-l₀)=ma

Or d’apres la condition d’equilibre : mg= k(leq-l₀)

Il s’en suit :

<=> – kx =ma

Sachant que :

On a :

On trouve une équation analogue a celle d’un pendule élastique horizontal.

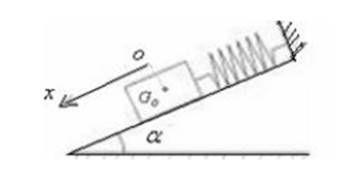
Cas du pendule élastique oblique

Dans un plan lisse incliné d’un angle α, on attache à l’extrémité d’un ressort de spires non jointives et de masse négligeables, un corps (S) de masse m, le ressort s’allonge donc d’une distance ∆l0, on la détermine en étudiant le système à l’équilibre :

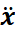
A l’équilibre,

En projectant suivant l’axe des x :

Psinα-T=0

Or T=kΔl₀, Δl₀ étant l’allongement du ressort

mgsinα=k Δl₀

Maintenant on écarte le corps et on le lâche sans vitesse initiale, il effectue un mouvement oscillatoire.

Dans le repère (Gx), on applique le TCI :

Psinα-T=m

Psinα-k(Δl₀ + x )=m

Psinα-k(Δl₀) -kx =m

-kx =m

Que le pendule soit horizontal, vertical ou oblique, la période des oscillations ne dépend que de la masse m du solide et de la raideur du ressort.

Etude énergétique d’un pendule élastique

E=constante

k en Nm-1

Xm en m

m en kg

E en joule

L’énergie mécanique d’un pendule élastique non amorti reste constante au cours des oscillations. Elle est proportionnelle au carré de l’amplitude.

EXERCICES

EXERCICE I :

Un pendule élastique est constitué d’un solide de masse m=200 g fixé à l’extrémité mobile d’un ressort de raideur k=5 N.m^-1. Il oscille autour de sa position d’équilibre avec a une amplitude de 5 cm.

A l’équilibre des dates, le centre d’inertie du solide occupe la position d’élongation maximale.

1.Calculer la pulsation propre ω₀ du système oscillant, puis déduire la période propre et la fréquence propre se son mouvement.

2.Donner les équations horaires de la position et de la vitesse du centre d’inertie du solide.

3.Determiner la vitesse maximale du centre d’inertie du solide.

EXERCICE II :

On considère un pendule élastique vertical constitué d'un ressort de constante de raideur k=20N/m et d'un corps solide de masse m=200g . On écarte le corps S verticalement vers le bas à partir de sa position d'équilibre d'une distance égale à 3cm et on le lâche sans vitesse initiale. A l'instant t=0 le corps passe de la position d'équilibre stable Go dans le sens positif.

1) Déterminer l'allongement du ressort à l'équilibre Δlo

2) Déterminer l'équation différentielle du mouvement.

3) Donner l'équation horaire du mouvement.

4) Déterminer la période propre du mouvement. On donne g=10N/kg.

EXERCICE III :

Un pendule élastique est placé sur un plan incliné d'un angle a = 30o par rapport au plan horizontal. Le pendule élastique est constitué d'un ressort maintenue par un support fixe à l'une de ses extrémités alors que l'autre extrémité est liée à un corps solide de masse de masse m=200g . (voir schéma). Sachant que l'allongement du ressort à l'équilibre est : Δlo = 8cm

1)Déterminer l'allongement de ressort à l’équilibre.

2) On écarte le corps de sa position d'équilibre de 2cm selon la ligne de la grande pente vers le bas et on le lâche sans vitesse initiale.

a- Déterminer l'équation différentielle du mouvement.

b-Sachant que le corps passe à t=0 du point d’abscisse x=+1cm dans le sens positif. Déterminer l'équation horaire du mouvement. On donne : g=10N/kg

EXERCICE IV :

Un ressort à spires non jointives, parfaitement élastique et de masse négligeable est suspendu verticalement. L’une de ses extrémités est fixe. A l’autre est attache un solide (S) de masse m=500 g et de centre d’inertie G. la raideur du ressort est de 20 N.m^-1. Les positions de G seront repérées par rapport à un axe vertical Ox. L’origine étant la position de G à l’équilibre.

1.Calculer l’allongement du ressort à l’équilibre.

2.On tire (S) verticalement vers le bas de 5 cm à partir de la position d’équilibre précédente et on le lâche sans vitesse initiale à la date t=0.

a-le solide (S) étant animé d’un mouvement de translation verticale, déterminer la nature du mouvement de G.

B-établir l’équation horaire de ce mouvement.

c-calculer la vitesse de G au passage en O.

On donne g=10 SI.

EXERCICE IV :

Situation-problème

Votre lycée vient de recevoir les matériels pour le laboratoire de physique. Un groupe d’élèves de terminale C se donne pour objectif de caractériser un ressort de constante de raideur k et un mobile de masse m.
Ce groupe d’élèves réalise le schéma du montage de l’oscillateur élastique horizontal sur banc à coussin d’air, représenté sur le document 1.
Les conditions initiales de travail sont :
• Abscisse initiale du centre d’inertie du mobile x0=4,0cm ; -vitesse initiale v0=0,0 m/s.
L’expression T=2π√mk est conservée dans la calculatrice.
Au cours de la manipulation, les données obtenues sont exploitées et des graphes tracés (documents 2 et 3). Le document 2 présente l’évolution de l’abscisse x du centre d’inertie G du mobile au cours du temps, tandis que le document 3 présente l’évolution de l’énergie potentielle élastique Epe du système {mobile + ressort} au cours du temps. Deux élèves de ce groupe, étant en désaccord sur la nature de l’oscillateur, s’accordent sur le fait que, quel que soit sa nature, la période de l’oscillateur sera confondue à la période propre d’un oscillateur idéal.
En exploitant les informations ci-dessus et à partir d’un raisonnement logique,
1. Départage les deux élèves. 
2. Prononce-toi sur les caractéristiques de cet oscillateur. Extrait de l‘ épreuve zéro de physique Théorique au baccalauréat D 2025 Région du Nord-Ouest

CORRIGES

EXERCICE I :

1. Sa pulsation propre :
=

Sa fréquence propre

=

Sa période propre est :

2. Equation horaire de la position du centre d’inertie :

A l’instant initial, donc

=> soit

L’expression de l’élongation a tout instant est : x(t)=5.10^-2sin(5t +π/2)

Equation horaire de la vitesse : v(t)= 5.10^-2x5cos(5t +π/2)= 25.10^-2 cos(5t +π/2)=

3.La vitesse maximale est v_max=x_mω₀=5.10^-2 x5=25.10^-2 m.s^-1.

EXERCICE II :

Le système étudié : le corps S à l'équilibre

Bilan des forces :

À l'équilibre le corps S est soumis à l'action des forces suivantes :

: son poids.

: la tension du ressort à l'équilibre.

D'après la condition d'équilibre du corps S on a donc:

To =P = m.g = KΔl₀ => Δl₀= m.g /K = 0,2 x 10/ 20 =0,1m=10 cm

2) -Le système étudié :{le corps S } lorsqu'il effectue des oscillations.

- Bilan des forces: pendant son mouvement le corps S est soumis à l'action des forces suivantes :

: son poids.

: la tension du ressort.

On considère un repère (O, ⃗i ) , son origine O est confondu avec le centre d'inertie G₀ du corps S à l'équilibre.

D’après le TCI :

Par projection sur l'axe ox on a:

P - T= ma <=>mg-kΔl=ma donc mg-k(Δl0 +x)=ma

<=>mg-k Δl₀-kx=ma

D’apres la condition d’equilibre,

mg= k Δl₀

donc -kx=ma avec

C'est l'équation différentielle du mouvement.

3.La solution de l'équation différentielle :

x¨ + K m x=0 est: x = xm .cos(ω₀ t + φ)

D'après les données on a : ω_o = √ m /K = √ 0,2 /20 = 10rad/s et xm =3cm

Et d'après les conditions initiales :

à t=0 , x=0 donc 0 = xm. cosφ

=> φ= ± π/ 2

de plus le corps passe de la position d'équilibre stable Go dans le sens positif donc v>0 à t=0.

Et on a: x = xm .cos(ω_o .t + φ) →

v = x˙ = -xm ω_o.sin(ω_o.t+φ) donc à t=0 :

v = -xm .ω o .sin φ> 0 → sinφ < 0 donc φ< 0

d’où: φ = - π/ 2

L'équation horaire du mouvement est :

x = 3.10^-2.cos(10.t - π /2 )

4) La période propre du mouvement. :

To = 2 π . √ m/ K = 2 π . √ 0,2/ 20 ≈ 0,628 s

EXERCICE III :

1) Système étudié {le corps solide à l’équilibre}

Bilan des forces:

: poids du cavalier.

: la tension du ressort à l'équilibre.

: réaction du plan de contact elle est perpendiculaire au plan de contact car les frottements sont négligeables.

Condition d'équilibre:

Par projection sur l'axe ox:

P.sin a – To +0 =0 → m.g.sin a - k.∆lo = 0 donc : ∆lo = m. g.sinα/ k

AN: ∆lo = 0,2.sin 30 x 10 /20 =0,05 m=5 cm

2) Système étudié {le corps solide}

Bilan des forces:

: poids du cavalier.

: la tension du ressort lors du mouvement.

: réaction du plan de contact elle est perpendiculaire au plan de contact car les frottements sont négligeables

En appliquant la deuxième loi de Newton:

Par projection sur l’axe ox:

Psinα-T=m

Psinα-k(Δl₀ + x )=m

Psinα-k(Δl₀) -kx =m

-kx =m

=>

1) la solution de cette équation différentielle est de la forme suivante:

x = xm .cos(ω o .t + φ ) avec :

ω o = √ m/ K = √ 0,2 20 = 10rad / s et xm = 2cm

Pour déterminer la valeur de φ, on utilise les conditions initiales :

à t=0, on a: x=1cm

En remplaçant dans (1) on a:

1 = 2.cos φ → cos φ = 1 /2

d’où: φ=cos ⁻¹ 1 /2 = ±π/ 3

Or le corps passe à t=0 du point d’abscisse x=+1cm dans le sens positif, donc sa vitesse v>0 à t=0.

Et on a : v = x˙ =-x. ω₀sin(ω₀.t+ φ ) et à t=o : v=-xm.ω₀sin φ >0

φ = - π/ 3 d' où : φ < 0 donc: sin φ < 0

Équation horaire du mouvement : x = 2. 10^-2 cos (10.t – π/3 )

EXERCICE IV :
Le système étudié : le corps S à l'équilibre

Bilan des forces :

À l'équilibre le corps S est soumis à l'action des forces suivantes :

: son poids.

: la tension du ressort à l'équilibre.

D'après la condition d'équilibre du corps S on a donc:

To =P = m.g = KΔl₀ =>

Δl₀= m.g /K = 0,5 x 10/ 20 =25 cm

2) a-Le système étudié :{le corps S } lorsqu'il effectue des oscillations.

- Bilan des forces: pendant son mouvement le corps S est soumis à l'action des forces suivantes :

: son poids.

: la tension du ressort.

On considère un repère (O, ⃗i ) , son origine O est confondu avec le centre d'inertie G₀ du corps S à l'équilibre.

D’après le TCI :

Par projection sur l'axe ox on a :

P - T= ma <=>mg-kΔl=ma

donc mg-k(Δl0 +x)=ma

<=>mg-k Δl₀-kx=ma

D’apres la condition d’equilibre,

mg= k Δl₀

donc -kx=ma avec

C'est l'équation différentielle du mouvement.

D'après les données on a : ω_o = √ m /K = √ 20 /0,5 = Ѵ40 rad/s

b-La solution de l'équation différentielle :

x¨ + K /m x=0 est: x = x_m .cos(ω₀ t + φ)

x_m=5 cm

Et d'après les conditions initiales :

à t=0 , x= x_m = xm. cosφ => φ= 0 (2π)

L'équation horaire du mouvement est :

x = 5.10^-2.cosѴ40t (s )

c- Premier passage en O a t₁=T₀/4= π/2ω₀

=>

Partie B : Évaluation des compétences / 16 points

Situation problème 1 / Étude d’un générateur / 8 points

Déterminons l’intensité du courant et la tension électrique délivrée par ce générateur puis comparons ces valeurs aux limites du courant et de la tension.
Déterminons l’intensité I du courant à partir de la première expérience en appliquant la condition d’équilibre à la barre.
D’après la condition d’équilibre
MΔ(→F)+MΔ(→R)+ MΔ(→P)=0
B×I×L2+0−mgL2sinα =0⇒I=mgsinαBL
AN : I=1,27A
Déterminons la tension électrique U à partir de la deuxième expérience en appliquant la condition d’équilibre à la boule.
tanα=FP=|q|Ud⇒ U=mg×d|q|tanα
AN : U=298,86V
{I≺2A|U|≺350V, Alors , il peut utiliser ce generateur.

Situation-problème 2 / 8 points

Avis sur la nature de l’oscillateur
Il s’agit de déterminer la nature de l’oscillateur afin de départager les deux élèves. Pour cela, nous allons :
(i) Exploiter les résultats des expériences pour déterminer la nature de l’oscillateur;
(ii) conclure.
D’après les documents 2 et 3, l’énergie et la position de l’oscillateur décroissent avec le temps ; la perte de l’énergie au cours du temps est du à la présence des forces de frottements ; ceci est une caractéristique d’un oscillateur réel (oscillateur libre et amorti)
Conclusion : au vu de ce qui précède, l’oscillateur en question est un oscillateur libre et amorti ; donc c’est l’élève qui aura dit que c’est un oscillateur libre et amorti qui a raison.

Avis sur les caractéristiques de l’oscillateur
Il s’agit de déterminer les caractéristiques (constante de raideur k du ressort et masse m du mobile) de l’oscillateur.
Pour cela, nous allons exploiter les résultats des expériences pour :
(i) déterminer la constante de raideur k à partir de l’énergie potentielle maximale de l’oscillateur ;
(ii) déterminer la période de l’oscillateur ;
(iii) déduire la masse m du mobile ;
(iv) conclure.
- détermination de la constante de raideur k:
d’après le document 3, EPe=2,4×10−3J ; alors,
EPe=12kx20⇒k =2Epex20=3N/m.
- détermination de la masse m du mobile :
T0=2π√mk⇒ m=kT204π2=0,0486kg
Conclusion : L’oscillateur en question est caractérisé par les grandeurs k et m de valeur respective : k=3N/m, m=0,0486kg

Avez-vous un exercice a proposer?Cliquez-ici