CHAMP MAGNETIQUE

Définition

          Un champ magnétique est une région de l’espace dans laquelle des objets ferromagnétiques sont soumis à des forces magnétiques.

Exemple : Champ créé par un aimant.

Un champ magnétique est caractérisé en chacun des points par une grandeur vectorielle appelée vecteur champ magnétique ou induction magnétique noté  dont les caractéristiques sont:

- Direction et sens :

On utilise l’aiguille aimantée pour les déterminer. Ainsi la direction du vecteur champ magnétique est celle de l’axe SN de l’aiguille aimanté.

 Le sens est de S vers N

- L’intensité du vecteur champ est mesurable et s’exprime en Tesla de symbole 𝐓 on la mesure avec un teslamètre ou une sonde de HALL.

Ordre de grandeur.

Champ magnétique	Ordre de grandeur
Champ Magnétique terrestre	210^-7𝑇 à 710^-3𝑇
Aimant Ordinaire	210^-3𝑇 à 510^-3𝑇
Aimant de haut-parleur	10^-3𝑇 à 0,5𝑇

Spectre magnétique

           Plaçons un barreau aimanté sous une plaque lisse en carton ou en verre. Saupoudrons la plaque de limaille de fer. Donnons-y quelques légères secousses en tapotant du doigt.

La limaille de fer s’organise selon des courbes appelées lignes de champ.

.

Définition :

           On appelle ligne de champ une courbe qui en chacun de ses points est tangente au vecteur champ magnétique. L’ensemble des lignes de champs constitue un spectre magnétique. L’exploration du spectre magnétique à l’aide d’une aiguille aimantée montre que celle-ci se positionne tangentiellement à la ligne de champ

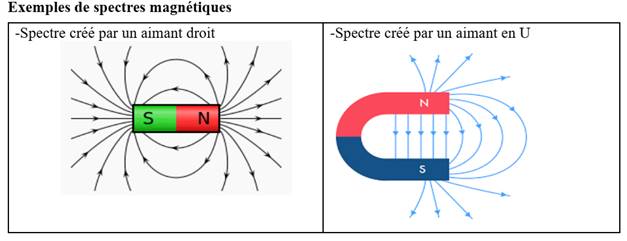
Définition d’un champ uniforme :

Un champ magnetique est dit uniforme quand le ecteur induction mgnetique    a même direction, même sens et même intensité en tout point de l’espace.

 Les lignes d’induction d’un champ magnétique uniforme sont des droites parallèles,

Exemple :  champ magnétique entre les branches d’un aimant en U.

Moment magnétique d’un aimant

L’action d’un champ magnétique sur un aimant se réduit à un couple. En effet, dans un champ magnétique, un aimant est soumis à un couple. Ainsi,    un aimant libre de se mouvoir, placé dans un champ magnétique uniforme, effectue un mouvement de rotation, donc il est soumis à un couple de force.  .

Le moment du couple magnétique M est proportionnel à l’induction magnétique B.

M = M.B.Sin𝜶

M = Moment magnétique de l’aimant en unités SI

B : Champ magnétique en tesla T

M: Moment du couple magnétique en m.N

Champ magnétique terrestre

              Dans une région peu étendue, le champ magnétique terrestre est uniforme. On peut déterminer l’induction terrestre d’un lieu à partir de :

-de la déclinaison D, angle du méridien magnétique avec le méridien géographique

-l’inclinaison I , angle que fait l’induction terrestre B avec le plan horizontal

-la composante horizontale B_H=Bo de l’induction terrestre, dont l’intensité est liée à celle de B par la relation :

B_o=BcosI

D : Déclinaison

I : Inclinaison

Bv : Composante verticale du champ magnétique terrestre

BH : Composante horizontale du champ magnétique terrestre

 : Champ magnétique terrestre.

EXERCICES

EXERCICE I :

En un point M de l’espace, se superposent deux champs magnétiques  et  crées par deux aimants dont les directions sont orthogonales. Leurs intensités sont respectivement B1 = 3.10^-3 T et B2 = 4.10^-3 T

1-Calculer l’intensité du champ résultant.

2-Calculer la valeur de l’angle qu’il fait avec le plan horizontal

EXERCICE II :

En lieu donné, la composante horizontale du champ magnétique terrestre a pour intensité B_h = 2.10^-5T et l’inclinaison I=64°

1. Préciser le sens du terme ‘’inclinaison’’

2. Déterminer l’intensité du champ magnétique terrestre du lieu

3. Calculer l’intensité B_v de la composante verticale en ce lieu.

4. La direction de la composante horizontale de B n’est pas exactement la direction sud-nord géographique du lieu. Le décalage est D = 50°

Que représente D ? On illustrera sa réponse par un schéma

EXERCICE III:

Deux bobines plates identiques de rayon R = 8 cm comportant 100 spires sont chacune traversée par un courant I = 2,5A et elles sont disposées à 8 cm de telle sorte que leurs axes soient confondus.

1. Comment appelle-t-on ce dispositif

2. Calculer le module du champ magnétique au centre O si les deux bobines sont traversées dans le même sens par le courant

EXERCICE IV:

Dans un champ magnétique uniforme dont l’induction magnétique  a pour intensité B = 5.10^-5T

1) On place une aiguille aimanté mobile autour de son centre de gravité : comment s’oriente-t-elle ?

2) On suspend un barreau aimanté par un fil métallique qui se tord quand le barreau tourne sous l’action du champ magnétique : quel est le moment magnétique du barreau, si le moment du couple de torsion vaut  m.N lorsque le barreau s’immobilise dans le champ quand son axe SN fait un angle de 45° avec l’induction magnétique  ?

3) Une petite aiguille aimantée, de moment magnétique 5.10^-3 unité SI, est suspendue par son centre de gravité en un point A d’un champ magnétique ; sachant que pour maintenir son axe magnétique Sn dans une direction perpendiculaire à celle de l’induction magnétique  au point A il faut lui appliquer un couple de moment M = 2.10^-5 n.M, calculer l’intensité de l’induction magnétique au point A.

Avez-vous un exercice a proposer?Cliquez-ici

Merci de votre visite
Laissez un commentaire