GENERALITES SUR LES SYSTEMES OSCILLANTS

SYSTEMES OSCILLANTS

a) Oscillateur mécanique

* Un système mécanique qui effectue un mouvement d'aller-retour de part et d'autre de sa position d'équilibre est dit oscillateur mécanique. Une oscillation est un aller-retour autour de la position d'équilibre.

* Exemples :

Mouvement des marées, battements du cœur, ...

b) Oscillateur libre

* C'est un oscillateur abandonné à lui-même après excitation extérieure.

* Exemples : pendule simple, pendule élastique, ...

c) Oscillateur harmonique

* C'est un oscillateur dont l'évolution dans le temps suit une loi sinusoïdale du temps.

* Exemples : pendule élastique sans frottement (cas idéalisé)

d) Oscillateur forcé

* C'est un oscillateur excité par un dispositif extérieur imposant le rythme d'oscillation.

* Exemples : mouvement des marées, haut-parleurs, ...

e) Oscillateur amorti

* C'est un oscillateur dont les oscillations s'affaiblissent au cours du temps.

* Exemples : pendule élastique réel, mouvement d'une corde de piano, ...

CARACTERISITIQUES D’UN SYSTEME OSCILLANT

Tous les systèmes oscillants évoluent au cours du temps de manière alternative et périodique.

La grandeur physique associée

Suivant que l’oscillateur est mécanique, électrique ou chimique, on lui associe une grandeur caractéristique g qui permet de décrire son évolution au cours du temps.

En mécanique, la grandeur physique associée peut être :la position x(t), la vitesse v(t), la force f(t)…

En électricité :la charge q(t), l’intensité i(t), la tension u(t)…

La relation g(t) qui décrit l’évolution de la grandeur caractéristique du système est appelée loi horaire du système oscillant.

Période et fréquence

La période T d’un système oscillant est la plus petite durée au bout de laquelle le phénomène se reproduit identique a lui-même. C’est la durée d’une oscillation.

T en seconde(s)

La fréquence f est le nombre de fois que le phénomène se répète pendant l’unité de temps. C’est l’inverse de la période.

f en hertz(hz)

Amplitude

L’élongation a désigne l’écart à un instant donnée entre la position considérée celle à l’équilibre. C’est une grandeur algébrique.

L’amplitude est la valeur absolue de l’élongation maximale. C’est une grandeur toujours positive.

Exemple : Soit l’oscillogramme ci-dessous.

Elongation : y=asin(ωt+φ)

Amplitude : a

Pulsation : ω

Phase à l’origine : φ

Phase à l’instant t quelconque : (ωt+φ)

REPRESENTATION DE FRESNEL

Vecteur de Fresnel

A tout vecteur tournant à vitesse ω constante autour de O, on peut associer une fonction sinusoïdale y représentant l’ordonnée de l’extrémité du vecteur tournant.

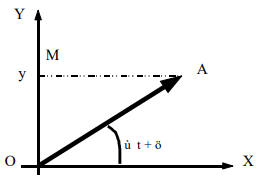
Projection d’un vecteur tournant

à la vitesse angulaire ω :

A l’instant t l’angle

vaut ωt+ φ

La projection de

donne y=asin sin(ωt+ φ)

Quand le point A tourne, le point M effectue un mouvement rectiligne sinusoïdal le long de l’axe.

Le vecteur tournant

est le vecteur de Fresnel, la norme de ce vecteur correspond à l’amplitude a de la fonction sinusoïdale et l’angle que fait

avec l’axe Ox correspond à la phase φ.

Somme de deux grandeurs sinusoïdales de même pulsation

Soient deux grandeurs sinusoïdales :

y₁=a₁sin sin(ωt+ φ₁) et y₂ =a₂sin(ωt+ φ₂).

La somme y₁+y₂ est une grandeur sinusoïdale de la forme Y=Asin(ωt+ Փ) ou A l’amplitude et Փ la phase a l’origine sont à déterminer.

Construction de Fresnel

Amplitude A

Le théorème de Pythagore appliqué au triangle quelconque OS₁S donne :

A²=S₁²+S₂²- 2S₁S₂cosα avec

= S₁²+S₂²-2S₁S₂cos(π-Δφ)

=a₁²+a₂²+2a₁a₂cos(φ₂-φ₁)

Phase Փ

Soient H₁, H₂ et H les projections orthogonales des points S₁, S₂ et S.

Comparaison de deux grandeurs sinusoïdales

Notion de déphasage

Deux grandeurs sinusoïdales peuvent être décalées. Le déphasage angulaire entre deux grandeurs :

y₁=a₁sin sin(ωt+ φ₁)

y₂ =a₂sin(ωt+ φ₂),

La différence de phase Δφ =φ₂-φ₁

· si Δφ =φ₂-φ₁>0, y₂ est en avance de phase sur y₁

Exemple : i₂ est en avance par rapport à i₁

· si Δφ =φ₂-φ₁<0, y₂ est en retard sur y₁

Exemple :

- i₂ est en retard par rapport à i₁

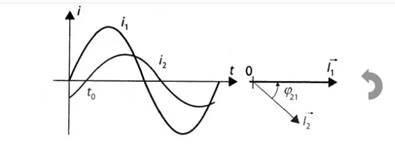
Le décalage horaire, directement lu sur le cadran d’un oscilloscope est donné en fonction du déphasage angulaire par la relation :

Déphasages particuliers

· Grandeur en phase

Deux grandeurs sont en phase quand le déphasage est :

Δφ =φ₂-φ₁=0 +2kπ

Les vecteurs de Fresnel correspondants sont colinéaires de même sens et l‘amplitude de la vibration résultante est égale à la somme des amplitudes :

a=a₁+a₂

Deux fonctions sinusoïdales en phase sont deux fonctions qui :

· S’annulent en même temps

· Passent par le maximum et le minimum en même temps

Exemple : u(t) et i(t) sont deux grandeurs en phase

· Grandeurs sinusoïdales en opposition de phase

Deux grandeurs sinusoïdales sont en opposition de phase quand leur déphasage est :

Δφ =φ₂-φ₁=π +2kπ

Les valeurs instantanées des vibrations sont opposées et l’amplitude de la vibration résultante est égale à la valeur absolue de la différence des amplitudes respectives :

a=|a₁-a₂|

Deux fonctions sinusoïdales en opposition de phase sont deux fonctions qui :

· S’annulent en même temps

· Quand l’une est au maximum, l’autre est au minimum et vice versa.

Exemple : u(t) et i(t) sont deux grandeurs en opposition de phase

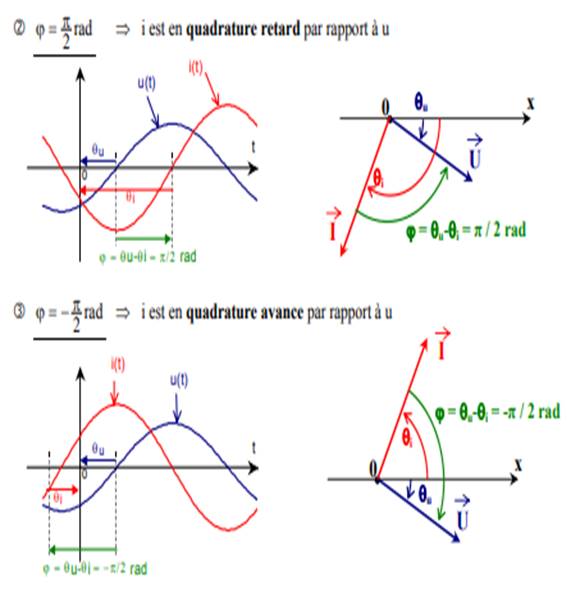
· Grandeurs en quadrature

Deux grandeurs sinusoïdales sont en quadrature quand le déphasage entre ces deux grandeurs est :

Δφ =φ₂-φ₁=π/2 +2kπ

L’amplitude résultante est donnée par la relation :

a² = a₁² + a₂²

Ces grandeurs peuvent être en quadrature avance ou en quadrature retard.

Deux fonctions sinusoïdales en quadrature de phase sont deux fonctions telles que si l’une passe par son maximum ou son minimum, l’autre passe par zéro et vice versa.

Exemple : u(t) et i(t) sont deux grandeurs en quadrature

METHODES D’ANALYSE DES SYSTEMES OSCILLANTS

-enregistrement graphique

-analyse a l’oscilloscope

-analyse stroboscopique

EXERCICES

EXERCICE I:

Soient deux grandeurs sinusoïdales u₁(t) et u₂(t), l’analyse a l’oscilloscope a donné l’oscillogramme suivant :

Déterminer :

1. Les amplitudes de u₁(t) et a₁ et a₂ de u₂(t).

2. La période T₁ de u₁(t) et la pulsation ω₁.

3. Calculer le déphasage entre les deux fonctions. Laquelle des deux fonctions est en avance sur l’autre ?

4. Quel est le décalage horaire entre les deux fonctions ?

EXERCICE II:

Déterminer par construction de Fresnel la somme des grandeurs sinusoïdales suivantes :

1. x₁=sin(ωt+π/6) et x₂=2sin(ωt +π/3) en cm

2. i₁=2sin(ωt+ π/6) et i₂=2cos(ωt +π/3) en A

3. u₁=sinωt et u₂=2sin(ωt +π/3) en V

EXERCICE III :

Soit la fonction alternative sinusoïdale représentée ci-dessous :

1 Indiquer sa période

2. Indiquer sa fréquence :

3.Sachant que sa phase à l’origine est un multiple de π/6 , préciser son expression analytique.

CORRIGES :

EXERCICE I :

1. Amplitude a₁ de u₁ : 4 divisions x100V/div=400V

Amplitude a₂ de u₂ : 3 divisions x50V/div=150 V

2. Période T₁ : 12 divisions x2ms/div=24 ms

Pulsation ω₁ : ω₁=2π/T=2π/24=π/12.10^-3 rad.s^-1

3. Décalage horaire : 2 divisions x 2 ms/div=4

4.

=>

u₁(t) est en avance sur u₂(t)

EXERCICE II:

Déterminer par construction de Fresnel la somme des grandeurs sinusoïdales suivantes :

1. x₁=sin(ωt+π/6) et x₂=2sin(ωt +π/3) en cm

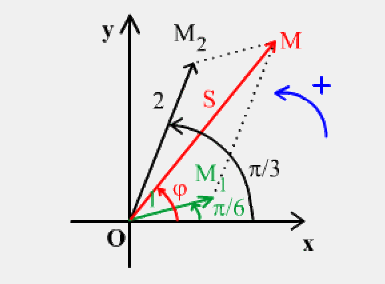
A²=1²+2² +2.1.2cos(π/3-π/6)=5+4cosπ/6=5+4.0,86=8,44 =>A=2,9 cm

φ=tan^-1(1,193)=50

2. i₁=2sin(ωt+ π/6) et i₂=2cos(ωt +π/3) en A

A²=2²+2² +2.2.2cos(π/3-π/6)=8+8cosπ/6=8+6,88 =>A=3,86 A

φ=tan^-1(1)=45

3. u₁=sinωt et u₂=2sin(ωt +π/3) en V

A²=1²+2² +2.1.2cos(π/3-π/6)=5+4cosπ/6=5+4.0,86=8,44 =>A=2,9 cm

φ=tan^-1(1,11)=48

EXERCICE III :

1 sa période : 2ms

2. sa fréquence : 1 /2.10^-3=500Hz

3.y=acos(ωt+φ)

a=5

ω=2πf=1000π

a t=o y=2,5 =>2,5=5cosφ =>cosφ=2,5/5=0,5 =>φ=π/3 +2kπ ou φ=-π/3 +2kπ

φ= π/3 car multiple de π/6 => y=5cos(1000πt+π/3)