ENERGIE MECANIQUE

I ENERGIE POTENTIELLE

On appelle énergie potentielle d’un système, l’énergie que ce système peut libérer en modifiant les positions relatives de ses éléments.

Exemple1 : L’eau stockée dans un barrage possède de l’énergie potentielle. En effet elle peut descendre et actionner les turbines d’une centrale hydroélectrique.

Exemple 2 : Un arc tendu possède de l’énergie potentielle en effet lâché, l’arc peut envoyer une flèche

Energie potentielle de la pesanteur

.C’est l’énergie que possède un corps du fait de sa position dans un champ de pesanteur.

Exemple : Une mangue accrochée à une branche possède de l’énergie potentielle si on considère le système formé par la mangue et la terre. En effet, si la mangue tombe, son poids effectue un travail proportionnel à la hauteur de chute . C’est une énergie de position.

Au cours de la chute de la mangue d’une hauteur h, l’énergie potentielle de pesanteur E_pp du système diminue d’une quantité égale au travail du poids :

E_pp=mgh

où g =9,81N/Kg est l’intensité de la pesanteur

REMARQUES :

i-L ’énergie potentielle de pesanteur d’un système formé par l’objet et la terre diminue lorsque se rapproche de la terre et augmente lorsqu’il s’en éloigne.

ii-L’ énergie potentielle de pesanteur est négative si l’objet est au-dessous du niveau pris arbitrairement comme état de référence.

Energie potentielle élastique

Cas d’un ressort

Lorsqu’on étire un ressort, le travail effectué représente l’énergie potentielle élastique emmagasinée par le ressort.

Soit x l’allongement du ressort

E_pel=1/2 kx²

où k est la constante de raideur du ressort.

Un fil de torsion tordu, un ressort spiral comprimé possède de l’énergie potentielle élastique.

Soit C la constante de torsion et θ l’angle de torsion,

Ep=1/2 Cθ²

ENERGIE MECANIQUE

Définition

L’énergie mécanique E d’un système est égale, à chaque instant, à la somme de son énergie cinétique et de son énergie potentielle :

E= Ep + Ec

Conservation de l’énergie mécanique d’un système

A et B étant deux points quelconques, l’énergie mécanique du système (corps-terre) garde toujours la même valeur au cours de la chute. On dit qu’elle se conserve

E_A = E_B

Variation de l’énergie mécanique d’un système

Très souvent, l’énergie mécanique n’est pas constante au cours du temps et décroit plus ou moins rapidement. Le système considéré est non-conservatif. L’apparition de la chaleur accompagne la diminution de l’énergie mécanique.

EXERCICES

EXERCICE I :
L’expression littérale de l'énergie potentielle de pesanteur d’un objet est Epp = mgz
Avec z = hauteur de l’objet par rapport à l’origine de mesure (le sol en général)
1. Préciser la signification des termes et leur unité.
2. Lors d'une figure de free-style, une kit surfeuse de masse m = 50 kg réussit à s'élever à 7,0 m au-dessus
de la mer. En prenant le niveau de la mer comme référence des énergies potentielles, calculer son énergie
potentielle de pesanteur au point le plus haut de son saut.

EXERCICE II:

Calculer l’énergie potentielle de pesanteur d’un corps de 30 g situé à 10m du sol dans chacun des cas suivants :

a)le niveau de référence est le sol.

b) le niveau de référence est à 5m au-dessus du sol.

On donne :g=10N/kg

EXERCICE III:

Pour provoquer un allongement d’un ressort de 0,20m, il faut exercer une force de 15N.

a) Calculer la constante de raideur de ce ressort.

b) Calculer l’énergie potentielle du ressort ainsi tiré.

EXERCICE IV:

Une barre de 10 cm est suspendue en son milieu à un fil de torsion vertical de constante (C). En exerçant perpendiculairement à la barre une force horizontale de 0,16N, on fait effectuer au système, une rotation de 45°.

a) Calculer la constante de torsion du fil.

b) Calculer l’énergie potentielle du système fil-barre.

EXERCICE V :
Calculer une valeur de vitesse
Une balle de golf de masse m = 45 g tombe en chute libre sans vitesse initiale d'une hauteur h = 10 m par
rapport au sol, choisi comme référence des énergies potentielles de pesanteur.
1. Quelle est la diminution de l'énergie potentielle de pesanteur de la balle entre la hauteur h et le sol?
2. Calculer la valeur de la vitesse de la balle lorsqu'elle arrive au sol.
3. En déduire la variation d'énergie cinétique de la balle.

EXERCICE VI :
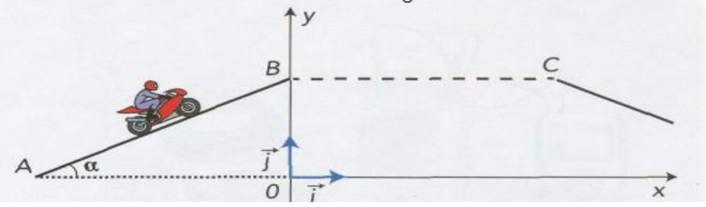
Le 31 mars 2008, l'Australien Robbie Madison a battu son propre record de saut en longueur à moto.
Soit un tremplin incliné d'un angle ɑ=27°
parcouru le tremplin AB avec une vitesse de valeur constante égale à 160 km.h^-1. Au point B, il s'est envolé pour un saut d'une portée BC = 107 m.
Entre B et C, toute force autre que le poids est supposé négligeable.
On choisit l'altitude du point A comme référence des énergies potentielles de pesanteur.
1. Exprimer l'énergie mécanique du système {motard + moto} en fonction de la valeur de la vitesse V et de l'altitude y.
2. Calculer l'énergie cinétique du système au point A.
3. a. Exprimer l'altitude yB du point B en fonction de AB et de a.
b. En déduire l'expression de la variation d'énergie potentielle de pesanteur du système, lorsque le système
passe du point A au point B. Calculer cette variation d'énergie.
c. Comment évolue l'énergie mécanique du système lorsqu'il passe de A à B? Justifier la réponse.
4. Comment évolue l'énergie mécanique du système lorsqu'il passe de B à C? Justifier la réponse.
5. En déduire sa vitesse au point C.
Données : • intensité de la pesanteur : g = 9,81 N.kg^-1 ; • masse du système : m = 180 kg; • AB = 7,86m.

EXERCICE VII :Dans une salle de jeu pour enfants, on trouve le dispositif présenté sur le document 1. Le principe de jeu consiste à placer le charriot (S) de masse m sur la piste rectiligne AC inclinée d'un angle a par rapport au plan horizontal et, de suivre son mouvement. Un enfant lâche le charriot au point A ( point le plus haut du plan incliné] sans vitesse initiale. Arrivé au point C avec une vitesse Vc, le charriot suit une trajectoire circulaire de rayon r et de centre 0. Malgré plusieurs essais, les enfants constatent que le charriot n'atteint pas le point D. La partie CD est en verre et supposée parfaitement lisse.
Un capteur est positionné au point C qui indique la valeur Vc vitesse du chariot.
Alain et Patrice élèves en classe de première D sont en désaccord sur la présence ou non des frottements sur la portion AC.
On supposera que le solide est ponctuel.
dispositif plan incline

1. En exploitant les informations ci-dessus, et en utilisant un raisonnement scientifique, départage Alain et Patrice.
2. En examinant le mouvement de S sur la portion CD et en utilisant correctement les informations données, prononce-roi sur la possibilité de S d’attendre le point D.
Données
α=30o, AC = 0,80 m ; r=30,0 cm, Vc=2,83 m/s ; g=10,0 et m = 50,0 g

Probatoire D et TI 2021

Partie Il : Évaluation des compétences / 16 points

Situation problème
Pour remonter les sacs de ciment un ingénieur propose deux possibilités à une entreprise.

Possibilité 1

Un "remonte-pente" motorisé pour tirer à vitesse constante les sacs de ciment de masse m=50kg vers le sommet d'un plan incliné AB d'un angle α=30o avec l'horizontale. La longueur du plan incliné est AB = 10 m. les essais effectués avec un sac de ciment pour différentes distances parcourues x ont donné les résultats suivants :

Essais	1	2	3	4	5	6
x [ en m ]	0,3	0,5	0,5	1,1	1,5	2,2
W(→F) [ en J ]	78; 75	131, 25	210	180, 75	393, 75	577, 5

Ou →F est la force motrice exercée sur le sac de ciment et parallèlement au plan incliné.
Avec le dispositif ainsi constitué, le ciment risque la déchirure lorsque la force frottement →f est supérieure à 15 N.
Le coût journalier en énergie électrique est de 700 Fcfa pour 3000 sacs de ciment.

Possibilité 2

Une poulie simple motorisée permettant de remonter les sacs de ciment à une hauteur de 5 m.
Le moteur consomme de l'énergie électrique donc le coût est de 75 Fcfa par KW.h.
On suppose que l'énergie électrique consommée pour les 3000 sacs de ciment journalier est égale au travail mécanique effectué.
Donnée: g: 10 lN/kg; 1kW.h =36×105 J

En exploitant les informations ci-dessus et en utilisant un raisonnement logique,
I-Examine l'utilisation du dispositif 1.
2- Aide le directeur de la société à faire un choix du dispositif le plus rentable.

CORRIGES:

EXERCICE I :.
1. m=masse en kg
g=accélération de la pesanteur
z=hauteur de l’objet en m
2. E_pp = mgz = 50 x 9,81x 7 = 3468,5 J

EXERCICE II:

a)E_p=mg(z-z₀), Au niveau du sol,

z₀=0 => E_p=mgz=0,3x10x0=30 J

b) E_p=mg(z-z₀) , .

z₀=5 => E_p=mg(z-5)=0,3x10(10-5)=15J.

EXERCICE III:

EXERCICE IV:

b) .

EXERCICE V :

1. Diminution de l'énergie potentielle de pesanteur de la balle entre la hauteur h et le sol

4. Calcul de la valeur de la vitesse de la balle lorsqu'elle arrive au sol.

Au début de la chute : Epp=mgh

Ec=0

A la fin de la chute : Epp=0

Ec=1/2mv²

L’énergie mécanique reste constante :

3. Variation d'énergie cinétique de la balle.

EXERCICE VI :

EXERCICE VII :

Le problème scientifique posé est de vérifier l'existence ou non des frottements sur la portion AC afin de départager les deux élèves.
Pour cela, nous allons :
• utiliser le théorème de l'énergie cinétique entre les points A et C pour déterminer la vitesse théorique (VC)th, du chariot en C en absence de frottement ;
• Comparer la valeur obtenue à celle indiquée par le capteur ;
• Conclure.
(i)- Détermination de (VC)th
En absence de frottement :
ΔEC=WAC(→P) +WAC(→R)
EC(C)−EC(A) =WAC(→P) =mgACsinα
Car →R⊥−−→AC et WAC(→R)=0
EC(C)= 12m(VC)2th
VA=0⇒ EC(A)=0
Soit
12m(VC)2th= mgACsinα⇒ (VC)th= √2gACsinα
(VC)th=2,83 m/s
(ii)- Comparaison
(VC)th=2,83 est égale à la vitesse indiquée par le capteur.
(iii)- conclusion
L'hypothèse de l'absence de frottement est confirmée, il n'y a pas de frottement sur la portion (AC).
Le problème posé est de vérifier si le chariot parti du point C avec la vitesse indiquée peut atteindre ou non le point D.
Pour cela nous allons :
• utiliser le TEC ou PCEM sur la portion CD pour déterminer la vitesse théorique (VD)th avec laquelle le chariot arriverait en D;
• interpréter le resultat obtenu et conclure
(i)- Détermination de (VD)th
• Forces : →P et →R.
Le TEC appliqué au chariot s'écrit :
EC(D)− EC(C)= WCD(→P)+ WCD(→R)
Avec WCD(→R)=0
12mV2D− 12mV2C= −2mgr
VD=√V2C−4gr =√−3,9911 impossible
(iii) Interprétation et conclusion
Le chariot ne pourra pas atteindre le point D.

Partie lI : Évaluation des compétences / 16 points

Examen de l'utilisation du dispositif 1
Il s'agit de déterminer la force de frottement pour vérifier si le transport des sacs de ciment peut se faire à l'aide du remonte pente sans déchirure.
Pour cela:
• Établir l'expression théorique du travail W(→F) de la force motrice en fonction de la longueur x du déplacement, en utilisant le théorème de l'énergie cinétique;
• Calculer la valeur expérimentale de la force de frottement ;
• La comparer à la valeur critique et conclure.
1.1. Bilan des forces
Un sac de ciment est soumis à :
• son poids →P;
• la réaction →R ;
• la force motrice →F ;
• la force de frottement →f supposée constante.
1.2.Expression du travail de la force motrice
D'après le théorème de l'énergie cinétique. ΔEC= ∑W(−−→Fext)
comme la vitesse est constante, on a : ∑W(−−→Fext)=0
Par ailleurs, W(→P)= −mgxsinα, W(−−→RN)=0 et W(→f)=−fx
Il vient donc :
W(→F)=x (mgsinα+f)
1.2. Valeur expérimentale de la force de frottement
Tableau de valeurs

Essais	1	2	3	4	5	6
x (en m)	0,3	0,5	0,8	1.1	1,5	2,2
W(→F) ( en J)	78, 75	131, 25	210	280, 75	393. 75	577, 5
W(→F)x ( en N)	262, 5	262, 5	262, 5	255, 2	262, 5	262, 5

La quatrième valeur de W(→F)x est à éliminer. On retient W(→F)x =262,5 N
Partant de W(→F)=x (mgsinα+f), on obtient f=W(→F)x −mgsinα
fexp=W(→F)x −250
AN : fexp=12,5 N
1.4. Comparaison: fexp≺15
Conclusion : Le dispositif 1 peut être utilisé.
Aide au choix du dispositif
Il s'agit ici de trouver le dispositif le plus rentable, en identifiant celui qui génère moins de dépense en énergie.
Pour cela :
• Calculer le travail mécanique effectué en utilisant une poulie simple ;
• Calculer le coût journalier correspondant ;
• Comparer au coût journalier associé au dispositif 1 et conclure.
2.1 Travail mécanique effectué en utilisant une poulie simple
Travail du poids d'un sac : W(−→P1)=−mgh
Wm=3000× ∣∣∣W(−→P1)∣∣∣= 3000mgh= 7,5×106J
2.2 Coût journalier pour le dispositif 2
Énergie électrique consommée : We=Wm= 7,5×106J= 2,08kWh
Coût: C2=75×Wm =156FCFA
2.3. Comparaison
Le coût journalier en énergie électrique est plus important avec la remonte pente inclinée qu'avec la poulie simple.
conclusion : Il est préférable d'utiliser la poulie simple.

Avez-vous un exercice à proposer ?Cliquez-ici