MOUVEMENT D'UNE PARTICULE DANS UN CHAMP MAGNETIQUE
Soit
une particule de charge q positive, animée d’une vitesse initiale ![]() ,
qui pénètre dans une région où règne un champ magnétique uniforme
,
qui pénètre dans une région où règne un champ magnétique uniforme ![]() .Le mouvement de la particule supposée
ponctuelle, de masse m et de charge électrique q est étudié dans le référentiel
de laboratoire considéré comme galiléen.
.Le mouvement de la particule supposée
ponctuelle, de masse m et de charge électrique q est étudié dans le référentiel
de laboratoire considéré comme galiléen.
Le
poids de la particule étant négligeable devant la force magnétique de Lorentz,
le TCI implique :
![]() =>
=> ![]()
Le
vecteur accélération est donc comme la force de Lorentz, toujours
perpendiculaire aux vecteurs ![]() et
et ![]()
Le
mouvement d’une particule chargée en mouvement dans un champ magnétique
uniforme est uniforme.
Cas ou le champ magnétique ![]() a la même direction que le vecteur vitesse
initiale
a la même direction que le vecteur vitesse
initiale![]()
Les deux vecteurs sont colinéaires donc
la force magnétique est nulle. L’accélération est aussi nulle et le vecteur
vitesse est constant en module, direction et sens. La particule est alors
animée d’un mouvement rectiligne uniforme.
![]()
Le mouvement est donc uniforme.
Cas ou le champ magnétique ![]() est orthogonal au vecteur vitesse initiale
est orthogonal au vecteur vitesse initiale![]()
L’intensité de la force centripète
générant le mouvement est donc :
![]()
![]()
R
en mètre(m)
m en kilogramme(kg)
v0 en mètre par seconde(m/s)
q en coulomb(C)
B
en tesla(T)
Tous les termes étant
constants, le rayon l’est aussi et la trajectoire est un cercle. Le mouvement
d’une particule se déplaçant dans un champ magnétique perpendiculaire a la
vitesse initiale est donc un mouvement circulaire uniforme.
La
vitesse angulaire de la particule est donnée par la relation :
![]()
La
période du mouvement circulaire est donc :
![]()
Elle
ne dépend pas de sa vitesse initiale.
Déflection magnétique
Des la sortie du champ en S, la
particule n’est plus soumise à aucune force et son mouvement devient rectiligne
uniforme. S P est le point d’impact de la particule sur un écran
perpendiculaire a une distance L du point o et A la projection du point O sur
l’écran. Déterminons la déviation magnétique D=AA’
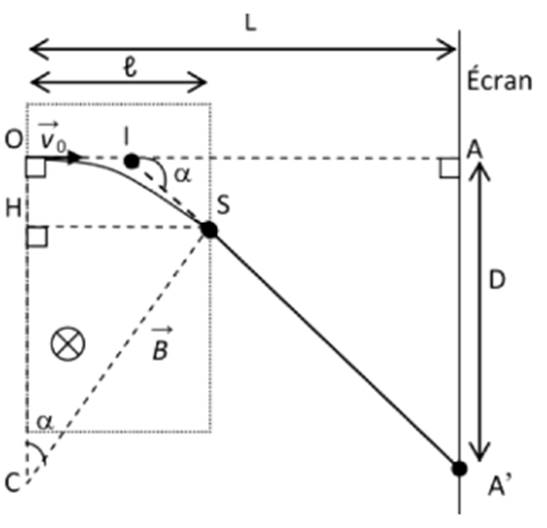
La déviation angulaire est donnée par
les relations :
![]()
Dans
les dispositifs à déflection magnétique, les angles sont petits et OI est très
petit devant L
Sinα
≈ tanα et IA=L-OI ≈ L
Donc :
![]() =
=![]()
![]()
La déflection
magnétique est proportionnelle à la valeur absolue de la charge et est
inversement proportionnelle à sa masse.
EXERCICES
EXERCICE I :
Un faisceau monocinétique d’électrons de vitesse v0=107m/s
pénètre en O dans un champ magnétique ![]() uniforme de largeur l=3 mm et
perpendiculaire à la direction de la vitesse des électrons.
uniforme de largeur l=3 mm et
perpendiculaire à la direction de la vitesse des électrons.
On mesure la
déflection magnétique sur un écran fixe E place perpendiculairement au
faisceau, a une distance L=40 cm du point d’entrée des électrons dans le champ.
On trouve Dm=4,5cm.
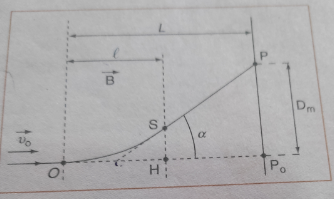
1. Donner l’expression du rayon de courbure de la trajectoire.
2. En utilisant les approximations utilisées, exprimer la déflection
magnétique Dm en fonction de L, l, B, e, m et v0.
3. Déterminer alors la valeur de ce champ magnétique et du rayon de
courbure.
EXERCICE
II :
Les ions hélium He2+ produits
dans une chambre d’ionisation sont captés en A, puis accélérés jusqu’en O, où
ils pénètrent dans un champ magnétique uniforme ![]() orthogonal à
orthogonal à
![]() . Ces particules
décrivent dans
. Ces particules
décrivent dans ![]() une trajectoire circulaire de rayon R. Le
poids des particules
une trajectoire circulaire de rayon R. Le
poids des particules
est négligeable
devant la force magnétique ![]() .
.
1-
Reproduire
la figure et représenter en O le vecteur force
Magnétique ![]()
2-En appliquant le
théorème du centre d’inertie à la particule dans ![]() ,
,
Calculer la valeur Vo de la vitesse en O. En déduire la valeur F
de
L’intensité
de la force magnétique.
2-
En
appliquant le théorème de l’énergie cinétique, calculer la valeur de la tension
accélératrice U entre A et O. Les ions partent en A avec une vitesse presque
nulle.
Données :
m=6,68.10-27 kg ; B=1,3T ; R=20cm ; e=-1,6.10-19
C.
EXERCICE III :
Un ion Li+ de vitesse v0 pénètre en O dans une zone
ou règne simultanément un champ électrique uniforme horizontale ![]()
et un champ magnétique horizontal ![]() .
. ![]() est
perpendiculaire au plan
(
est
perpendiculaire au plan
(![]() . Le champ de pesanteur est négligée.
. Le champ de pesanteur est négligée.
1.Donner la
direction, le sens et l’expression littérale de la force électrique ![]() s’exerçant sur l’ion Li+,
pénétrant dans cette zone.
s’exerçant sur l’ion Li+,
pénétrant dans cette zone.
2.Donner la direction,
le sens et l’expression littérale de la force électrique ![]() s’exerçant sur l’ion Li+,
anime de la vitesse
s’exerçant sur l’ion Li+,
anime de la vitesse![]() .
.
3. L’ion Li+ sort de cette zone sans subir de déviation. Déterminer
la relation existante alors entre les valeurs E, B et V0.
4. On supprime le champ ![]() . Calculer le
rayon du cercle alors décrit par cet ion et sa période de révolution.
. Calculer le
rayon du cercle alors décrit par cet ion et sa période de révolution.
V0=2.105m/s ;
masse de Li+=1,17.10-26kg ; B=0,5T.
.
EXERCICE IV :
Situation
problème
Au cours d’un concours scientifique, deux tâches sont proposées à chaque groupe
de deux candidats. Lors du passage du groupe constitué de AKONO et BENJl, les tâches suivantes leur sont proposés : '
Il leur est demandé de déterminer la tension U entre les
plaques P1P2; qui permet de
loger, les ions Br− dans le trou P après avoir été
successivement accélérés entre O et A et subit une
déviation sous l'effet du champ magnétique (voir figure ci-dessous)

Les deux amis
proposent les résultats différents. AKONG propose U=1,00×103V et le
BENJI propose U=1,00×102V.
Informations utiles :
Sur la déviation des ions
Les ions entrent dans la chambre d'accélération par le point 0 sans vitesse
initiale.
Expression du rayon de courbure de la trajectoire des ions : 
Données: AP = 0,811 m; B
= 0,1 T; q=−1,6×10−19
C, m=1,31×10−25 kg
En exploitant tes informations ci-dessus et à l'aide d'une démarche
scientifique,
Aide les deux candidats à choisir le bon résultat. (BACCALAUREAT D 2024 extrait)
CORRIGES
EXERCICE
I :
1.Expression
du rayon de courbure de la trajectoire.
Dans la
base de Frenet, les composantes de l’accélération sont :
at=0 et 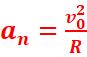
L’intensité
de la force centripète générant le mouvement est donc :
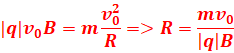
2.
expression de la déflection magnétique Dm en onction de L, l, B, e,
m et v0.
La
déviation angulaire α est donnée par :
![]()
Dans
les dispositifs de déflection magnétique, les angles sont petits et OI est
beaucoup plus petit que L
Alors
![]()
3.
Valeur de ce champ magnétique et de R.
![]() =
=![]()
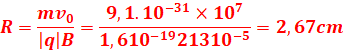
EXERCICE II :
1.
2-Calcul de la vitesse
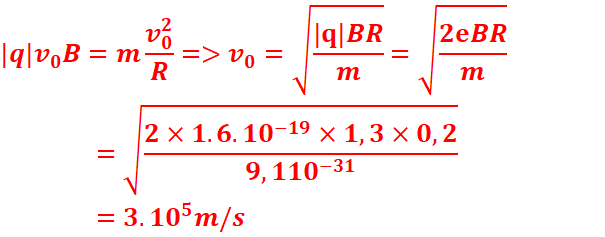
![]()
3.Calcul de la tension U
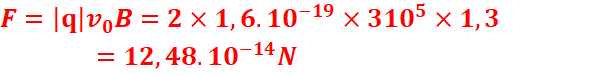
EXERCICE
III :
1. ![]()
![]() et
et ![]() ont même direction et même sens et on a : F=eE
ont même direction et même sens et on a : F=eE
2. ![]() ;
;
![]() est à la fois perpendiculaire a
est à la fois perpendiculaire a ![]() et a
et a ![]() ; comme e>0
; comme e>0
![]() est vertical et dirige vers le bas et
Fm=ev0B
est vertical et dirige vers le bas et
Fm=ev0B
3. ![]()
=>Fe=Fm <= > eE= ev0B=>E=v0B
4. ![]()
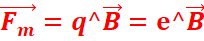
EXERCICE IV :
Il s'agit de déterminer la tension électrique
entre les plaques P1 et P2 afin d’aider les deux candidats
à choisir le bon résultat.
Pour cela, nous allons :
(i) Calculer le rayon de courbure R de la trajectoire circulaire.
(ii) Utiliser l'expression du rayon de L courbure
donnée pour déterminer la vitesse au point A ;
(iii) Utiliser le théorème de l'énergie cinétique pour déduire la tension entre
les plaques P1 et P2 ;
(iv) Comparer la valeur obtenue aux valeurs des deux candidats et conclure.
Rayon de courbure
R=AP2
AN : R=0,4055m
Vitesse du point A : R=mV/|q|B⇒V=R/|q|Bm
AN : V=49526,7 m/s
Tension entre les plaques P1 et P2
Le TEC appliqué à l’ion entre les points O et A:
ECA−EC0=W(![]() )⇔ 1/2mV2−0=|q|U
)⇔ 1/2mV2−0=|q|U
Soit U=mV2/2|q|
AN : U=1,004×10−3 V
Comparaison et conclusion
U=1,004×10−3V , donc le bon résultat est celui du candidat AKONO